【聚类3】密度聚类+层次聚类
文章目录
- 1. 密度聚类
-
- 1.2 DBSCAN算法
- 1.3 DBSCAN算法伪代码
- 1.4 DBSCAN算法生成聚类簇的步骤
- 2. 层次聚类
-
- 2.2 豪斯多夫距离
- 2.3 AGNES算法
- 2.4 AGNES算法伪代码
- 2.5 例子
1. 密度聚类
1.1 概念
- "别名":
基于密度的聚类
- "英文":
Density-based clustering
- "思想":
此类算法假设聚类结构能够通过样本分布的紧密程度确定
- "解释思想":
就是说,密度聚类算法从样本的密度角度来考察样本之间的可连续性(样
本之间可连续性代表簇的纯度越纯),并基于可连续样本不断拓展聚类簇,以
获得最终的聚类结果。
- "欧式距离":
在本节中,默认距离为欧式距离。
1.2 DBSCAN算法
- dbscan思想
DBSCAN是一种著名的密度聚类算法,它基于一组"邻域(neighborhood)参数",来刻画样本分布的紧密程度。
- 重要概念
| 已知 | D={ x 1 , x 2 , . . . , x m x_1,x_2,...,x_m x1,x2,...,xm} | 性质 |
|---|---|---|
| ε \varepsilon ε-邻域 | 包含样本集D中与 x j x_j xj的距离不大于 ε \varepsilon ε的样本,即 N ε ( x j ) = { x i ∈ D ∣ d i s t ( x i , x j ) ≤ ε } N_{\varepsilon}(x_j)=\{x_i\in D|dist(x_i,x_j)\leq\varepsilon\} Nε(xj)={xi∈D∣dist(xi,xj)≤ε} | |
| 核心对象(core object) | 若 x j x_j xj的 ε \varepsilon ε-邻域至少包含MinPts个样本,则 x j x_j xj是一个核心对象。即 ∣ N ε ( x j ) ∣ ≥ M i n P t s |N_{\varepsilon}(x_j)|\geq MinPts ∣Nε(xj)∣≥MinPts | |
| 密度直达(directly density-reachable) | 若 x j x_j xj位于 x i x_i xi的 ε \varepsilon ε-邻域,且 x i x_i xi是核心对象,则称 x j x_j xj由 x i x_i xi密度直达 | 不满足对称性 |
| 密度可达(density-reachable) | 对 x i x_i xi与 x j x_j xj,若存在样本序列 p 1 , p 2 , . . . , p n , 其 中 p 1 = x i , p n = x j 且 p i + 1 由 p i 密 度 直 达 p_1,p_2,...,p_n,其中p_1=x_i,p_n=x_j且p_{i+1}由p_i密度直达 p1,p2,...,pn,其中p1=xi,pn=xj且pi+1由pi密度直达,则称 x j 和 x i x_j和x_i xj和xi密度可达 | 直递性,不满足对称性 |
| 密度相连(density-connected) | 对 x i x_i xi与 x j x_j xj,若存在 x k 使 得 x i 与 x j 均 由 x k x_k使得x_i与x_j均由x_k xk使得xi与xj均由xk密度可达,则称 x i 和 x j x_i和x_j xi和xj密度相连 | 对称性 |
| 噪声(noise)或异常样本(anomaly) | D中不属于任何簇的样本认为是噪声或异常样本 |
- DBSCAN的簇定义
文字:
由密度可达关系导出的最大的密度相连样本集合
数学:
给 定 邻 域 参 数 ( ε , M i n P t s ) 给定邻域参数(\varepsilon,MinPts) 给定邻域参数(ε,MinPts)
簇 C ⊆ D , 满 足 以 下 性 质 : 簇C\subseteq D,满足以下性质: 簇C⊆D,满足以下性质:
连 接 性 ( c o n n e c t i v i t y ) : x i ∈ C , x j ∈ C → → x i 与 x j 密 度 相 连 \ \ \ \ \ \ \ \ \ 连接性(connectivity):x_i\in C,x_j \in C\rightarrow\rightarrow x_i与x_j密度相连 连接性(connectivity):xi∈C,xj∈C→→xi与xj密度相连
最 大 性 ( m a x i m a l i t y ) : x i ∈ C , x j 由 x i 密 度 可 达 → → x j ∈ C \ \ \ \ \ \ \ \ \ 最大性(maximality):x_i\in C,x_j由x_i密度可达\rightarrow\rightarrow x_j\in C 最大性(maximality):xi∈C,xj由xi密度可达→→xj∈C
- 基于上述性质的聚类的簇
文字:
若x为核心对象,由x密度可达的所有样本组成的集合,这个集合就是一个簇。
数学:
X = { x ′ ∈ D ∣ x 为 核 心 对 象 ⋂ x ′ 由 x 密 度 可 达 } X=\{x'\in D|x为核心对象\bigcap x'由x密度可达\} X={x′∈D∣x为核心对象⋂x′由x密度可达}
( 因 为 X 满 足 连 接 线 和 最 大 性 , X 就 是 想 要 的 簇 ) (因为X满足连接线和最大性,X就是想要的簇) (因为X满足连接线和最大性,X就是想要的簇)
1.3 DBSCAN算法伪代码
1.4 DBSCAN算法生成聚类簇的步骤
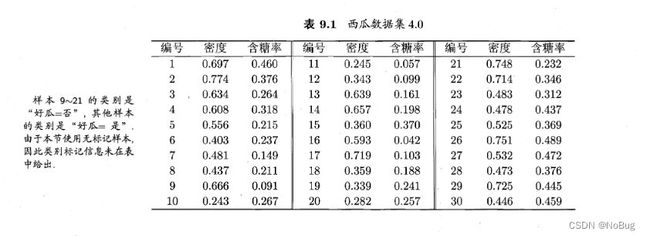
- 给定西瓜集:D
- 假定邻域参数 ( ε , M i n P t s ) (\varepsilon,MinPts) (ε,MinPts)
ε \varepsilon ε = 0.11
MinPts = 5
- 找出各样本的 ε \varepsilon ε 邻域
"方法:"
1. 可以利用DBSCAN算法
2. 直观来说:对每一个样本(例如:x_j)算它到剩余样本的欧式距离
3. 小于等于 ε 邻域的样本集合,构成x_j的领域
- 确定核心对象集合 Ω \Omega Ω
"方法:"
1. 若样本的邻域中样本的个数大于等于MinPts
2. 则这个样本是核心对象
3. 核心对象组成的集合,叫核心对象集合,用 Ω 来表示
本题中,核心对象集合为:
Ω = { x 3 , x 5 , x 6 , x 8 , x 9 , x 13 , x 14 , x 18 , x 19 , x 24 , x 25 , x 28 , x 29 } \Omega=\{x_3,x_5,x_6,x_8,x_9,x_{13},x_{14},x_{18},x_{19},x_{24},x_{25},x_{28},x_{29}\} Ω={x3,x5,x6,x8,x9,x13,x14,x18,x19,x24,x25,x28,x29}
- 从 Ω \Omega Ω 中随机选取一个核心对象作为种子
例如:选取 x 8 x_8 x8
- 找出由种子( x 8 x_8 x8)密度可达的所有样本
"方法:"
1. 要理解两个概念:
2. 密度直达
3. 密度可达
4. 所有样本构成一个聚类簇
本题中,第一个聚类簇为:
C 1 = { x 6 , x 7 , x 8 , x 10 , x 12 , x 18 , x 19 , x 20 , x 23 } C_1=\{x_6,x_7,x_8,x_{10},x_{12},x_{18},x_{19},x_{20},x_{23}\} C1={x6,x7,x8,x10,x12,x18,x19,x20,x23}
- 将聚类簇中包含的核心对象从 Ω 中去除
更新 Ω :
Ω = { x 3 , x 5 , x 9 , x 13 , x 14 , x 24 , x 25 , x 28 , x 29 } \Omega=\{x_3,x_5,x_9,x_{13},x_{14},x_{24},x_{25},x_{28},x_{29}\} Ω={x3,x5,x9,x13,x14,x24,x25,x28,x29}
- 结束标志是 Ω 为空集
给出例题结果:
C 1 = { x 6 , x 7 , x 8 , x 10 , x 12 , x 18 , x 19 , x 20 , x 23 } C_1=\{x_6,x_7,x_8,x_{10},x_{12},x_{18},x_{19},x_{20},x_{23}\} C1={x6,x7,x8,x10,x12,x18,x19,x20,x23}
C 2 = { x 3 , x 4 , x 5 , x 9 , x 13 , x 14 , x 16 , x 17 , x 21 } C_2=\{x_3,x_4,x_5,x_{9},x_{13},x_{14},x_{16},x_{17},x_{21}\} C2={x3,x4,x5,x9,x13,x14,x16,x17,x21}
C 3 = { x 1 , x 2 , x 22 , x 26 , x 29 } C_3=\{x_1,x_2,x_{22},x_{26},x_{29}\} C3={x1,x2,x22,x26,x29}
C 4 = { x 24 , x 25 , x 27 , x 28 , x 30 } C_4=\{x_{24},x_{25},x_{27},x_{28},x_{30}\} C4={x24,x25,x27,x28,x30}
2. 层次聚类
2.1 概念
- "英文:"
Hierarchical Clustering
- "思想"
在不同的层次对数据集进行划分
- "特点:"
形成的是树形的聚类结构
- "划分策略:"
1. 自底向上
2. 自顶向下
- "代表算法:"
AGNES(AGglomerative NESting)算法
2.2 豪斯多夫距离
- 概念
- "英文:"
Haosdorff Distance
也称:Pompeiu-Hausdorff距离
- "用处:"
1. 集合之间的距离度量
2. 计算两个集合之间的距离
- "原理:"
一个集合到另一个集合中最近点的最大距离
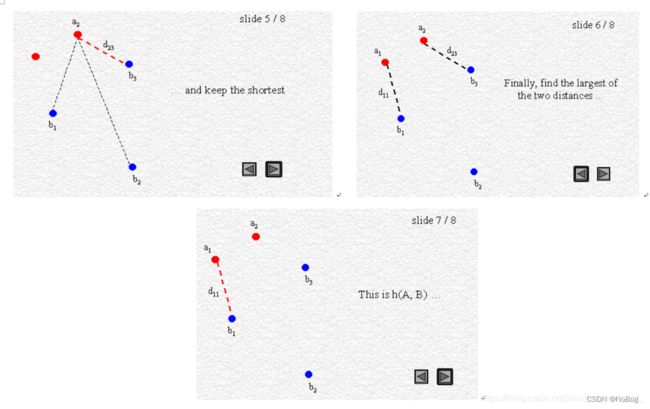
- 公式
h ( A , B ) = m a x a ∈ A { m i n b ∈ B { d ( a , b ) } } h(A,B)=max_{a\in A}\{min_{b\in B}\{d(a,b)\}\} h(A,B)=maxa∈A{minb∈B{d(a,b)}}
d ( a , b ) 一 般 为 欧 式 距 离 d(a,b)一般为欧式距离 d(a,b)一般为欧式距离
- 图例
2.3 AGNES算法
- 算法思想
"步骤:"
1. AGENS算法:是一种自底向上聚合策略的层次聚类算法
2. 先将数据集中每个样本看作一个初始聚类簇
3. 把距离最近的两个聚类簇进行合并
4. 不断重复,直至达到预设的聚类簇个数
"关键:如何计算关于集合的某种距离?"
1. 豪斯多夫距离
2. 最小距离
3. 最大距离
4. 平均距离
- 最小/最大/平均距离
公式:
最 小 距 离 : d m i n ( C i , C j ) = m i n x ∈ C i , z ∈ C j d i s t ( x , z ) 最小距离:d_{min}(C_i,C_j)=min_{x\in C_i,z\in C_j}dist(x,z) 最小距离:dmin(Ci,Cj)=minx∈Ci,z∈Cjdist(x,z)
最 大 距 离 : d m a x ( C i , C j ) = m a x x ∈ C i , z ∈ C j d i s t ( x , z ) 最大距离:d_{max}(C_i,C_j)=max_{x\in C_i,z\in C_j}dist(x,z) 最大距离:dmax(Ci,Cj)=maxx∈Ci,z∈Cjdist(x,z)
平 均 距 离 : d a v g ( C i , C j ) = 1 ∣ C i ∣ ∣ C j ∣ ∑ x ∈ C i ∑ z ∈ C j d i s t ( x , z ) 平均距离:d_{avg}(C_i,C_j)=\frac{1}{|C_i||C_j|}\sum_{x\in C_i}\sum_{z\in C_j}dist(x,z) 平均距离:davg(Ci,Cj)=∣Ci∣∣Cj∣1x∈Ci∑z∈Cj∑dist(x,z)
- 链接算法
AGNES算法的核心就是集合间的距离,
所以距离函数d(),十分重要。
不同的距离,AGNES算法名称也不同
1. 用d_min时:AGNES算法被称为"单链接"(single-linkage)算法
2. 用d_max时:AGNES算法被称为"全链接"(complete-linkage)算法
3. 用d_avg时:AGNES算法被称为"均链接"(average-linkage)算法