STL中vector建立最大堆和最小堆
1.堆的概念:
堆是一种非线性结构,可以把堆看作一个数组,也可以被看作一个完全二叉树,通俗来讲堆其实就是利用完全二叉树的结构来维护的一维数组按照堆的特点可以把堆分为大顶堆和小顶堆
- 大顶堆:每个结点的值都大于或等于其左右孩子结点的值
- 小顶堆:每个结点的值都小于或等于其左右孩子结点的值
(堆的这种特性非常的有用,堆常常被当做优先队列使用,因为可以快速的访问到“最重要”的元素)
2.heap性质
heap本质是用一个数组表示的完全二叉树,并且父节点总是大于(或者小于)子节点的值。在STL中用于实现优先队列(priority_queque)。堆排序是排序算法中是稳定效率最高的一种。STL以可以动态扩容的vector作为heap的底层数组。
一、建堆
vector<int> nums = {9, 6, 2, 4, 7, 0, 1, 8, 3, 5};
- 如果使用nums构建最大堆:(堆首为最大值)
make_heap(nums.begin(), nums.end());//默认建的为最大堆
//或
make_heap(nums.begin(), nums.end(), less<int>());
- 输出nums的结果为
9 8 2 6 7 0 1 4 3 5
2、如果使用nums构建最小堆:
make_heap(nums.begin(), nums.end(), greater<int>());
- 输出nums的结果为
0 3 1 4 5 2 9 8 6 7
将front(即第一个最大元素)移动到end的前部,同时将剩下的元素重新构造成(堆排序)一个新的heap。
时间复杂度是: (2*log(last - first))
二、调整堆
当使用上述的make_heap()建完堆后,如果vector使用push_back()插入数据或pop_back()删除数据后,会破坏最大堆/最小堆的性质,所以需要调整堆,常用push_heap()和pop_heap()两个方法
更新堆
push_heap()用法是,vector先push_back(),后push_heap():
nums.push_back(10);
push_heap(nums.begin(), nums.end(), less<int>());
- 输出nums的结果:
//原vector
9 8 2 6 7 0 1 4 3 5
//push_back()后
9 8 2 6 7 0 1 4 3 5 10
//push_heap()后
10 9 2 6 8 0 1 4 3 5 7
- push_heap分析
为满足完全二叉树的条件,新加入元素一定要放在最下一层作为叶子节点,并填补由左至右的第一个空格,也就是把新元素插入到底层vector的end()处。下图是push_heap算法的实际示意图:
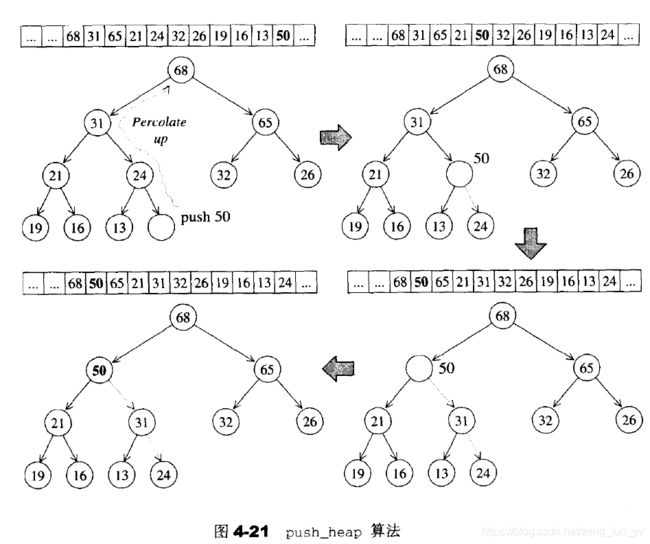
从图中可以看出push_heap算法的过程是将新加入堆的值(50),层层上挪,直到正确的位置。
删除堆首元素
pop_heap()用法是,先pop_heap(),vector后pop_back():
pop_heap(nums.begin(), nums.end(), less<int>());
nums.pop_back();
输出nums的结果:
//原vector
9 8 2 6 7 0 1 4 3 5
//pop_heap()后
8 7 2 6 5 0 1 4 3 9
//pop_back()后
8 7 2 6 5 0 1 4 3
原理:堆其实就是把vector内的元素最大值或最小值转移到nums[0]上。而pop_heap()是将nums[0]放到堆尾部,继而调用vector清除队尾
- pop_heap分析
pop_heap操作取走根节点,其实是移至底部容器vector的最后一个节点处并保存该节点。而此时需要维护vector.size()-1大小堆,需要为保存的节点在堆中找一个适当的位置。这个过程和上面的__push_heap的过程恰好相反,从根节点(此时为洞节点),层层下放,直到叶子节点位置,然后在这个位置调用push_heap加入刚刚保存的新值。下面是pop_heap算法实际示意图: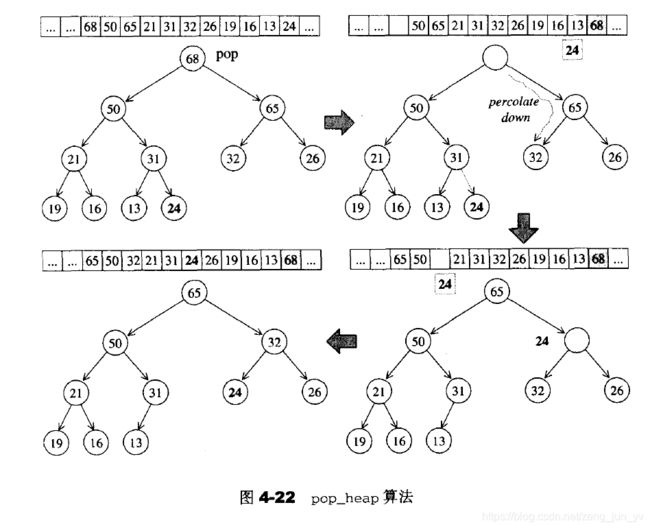
为什么pop_heap()的用法要反过来呢?
要从我们的目的来考虑,使用pop_heap()的绝大部分目的是要把堆顶元素pop出堆中,因为它最大或最小。如果先用vector的pop_back(),它删除的不是堆顶元素(nums[0]),而是vector的最后一个元素。可见这不是我们想要的结果:对于最大堆,最后一个元素既不是最大,也不一定是最小;对于最小堆,最后一个元素既不是最小,也不一定是最大。pop出来没有意义。
观察pop_heap()对堆做了什么?
pop_heap()把堆顶元素放到了最后一位,然后对它前面的数字重建了堆。这样一来只要再使用pop_back()把最后一位元素删除,就得到了新的堆。
堆简介
堆并不是STL的组件,但是经常充当着底层实现结构。比如优先级队列(Priority Queue)等等。
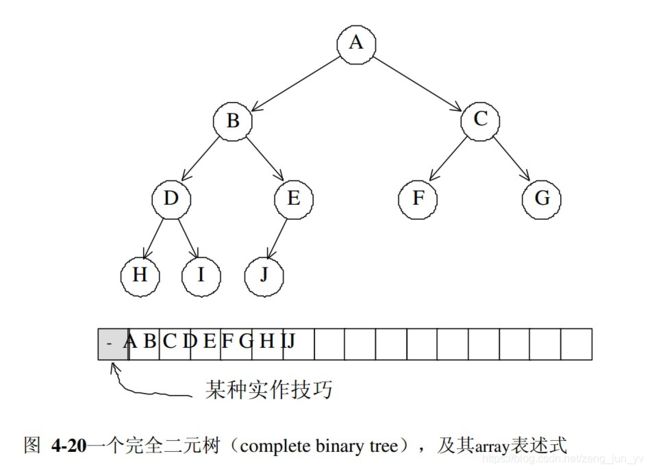
- 堆是一种完全二叉树,因此我们可以用数组来存储所有节点。在这里的实现中,采用了一个技巧:将数组中索引为0的元素保留,设置为极大值或者为极小值(依据大顶堆或者小顶堆而定)。那么当某个节点的索引是i时,其左子节点索引为2i,右子节点索引为2i+1.父节点是i/2(这里/表示高斯符号,取整)。这种以数组表示树的方式,我们成为隐式表述法(implicit reprentation)。我们这里用C++ STL中的容器vector实现替代数组的功能。
堆的主要相关算法介绍
- push_heap算法
此操作是向堆中添加一个节点。为了满足完全二叉树的条件,新加入的元素一定放在最下面的一层作为叶节点,并填补在由左至右的第一个空格,在这里放在底层容器vector的end()处。
很显然,新元素的加入很可能使得堆不在满足大顶堆的性质—每个节点的键值都大于或等于其子节点的键值。为了调整使得其重新满足大顶堆的特点,在这里执行一个上溯(percolate up)操作:将新节点与父节点比较,如果其键值比父节点大,就交换父子的位置,如此一直上溯,直到不需要交换或者到根节点为止。 - pop_heap算法
此操作取走根节点,放在底端。然后对比第二层的B、C大(假设对比规则是“a>b”)的枝干放在前面,小的放在后面。
例如:
如果: B > C
则结果是: BDEHIJ + CFG + A
PS:只对比一次
-
make_heap算法
此操作是依据已有的各元素构建堆。
其中,各元素已经存放在底层容器vector中。
构建堆实质是一个不断调整堆(即前面pop_heap算法中的调整堆的操作)的过程—通过不断调整子树,使得子树满足堆的特性来使得整个树满足堆的性质。
叶节点显然需要调整,第一个需要执行调整操作的子树的根节点是从后往前的第一个非叶结点。从此节点往前到根节点对每个子树执行调整操作,即可构建堆。 -
sort_heap算法
堆排序算法。执行此操作之后,容器vector中的元素按照从小到大的顺序排列。
构建大顶堆之后,不断执行pop_heap算法取出堆顶的元素,即可。因为每次取得的是最大的元素,将其放在容器vector的最尾端。所以到最后vector中的元素是从小到大排列的。
PS: sort_heap时,必须先是一个堆(两个特性:1、最大元素在第一个 2、添加或者删除元素以对数时间),因此必须先做一次make_heap.
参考1
参考2