PyTorch深度学习入门 || 系列（一）

0 写在前面

1. 之前通过观看b站视频，浅学了一些关于PyTorch的知识，现在希望基于书本，将之前所学的知识融会贯通起来。
2. 本篇文章旨在记录学习过程，并且用通俗易懂的语言将自己的理解表达出来！
3. 如果这篇文章对你有帮助的话，谢谢点赞关注收藏噢！

1 准备pytorch

这里默认大家已经在Windows系统下，配置了PyTorch！

2 Tensor基础知识

2.1 如何创建和操作Tensor

1. Tensor是PyTorch中进行数据存储和运算的基本单元。
2. Tensor之于PyTorch，相当于Array之于Numpy。
3. Tensor，中文名叫张量，是PyToch中最基本的数据类型。
4. 我们之前学习的标量、向量、矩阵都是张量的特例，标量是零维张量，向量是一维张量，矩阵是二维张量。张量还有三维、四维…甚至更多维！

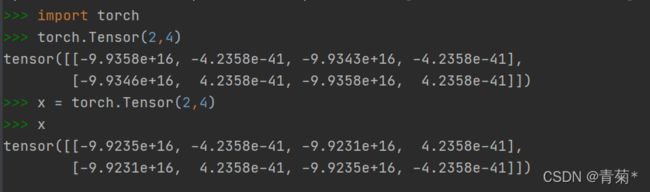
2.1.1 基本创建方法：torch.Tensor()

• x = torch.Tensor(2,4)
• 创建一个2*4的矩阵。
• 虽然没有初始化，但是这个矩阵中已经有值了。类型是32为float
  

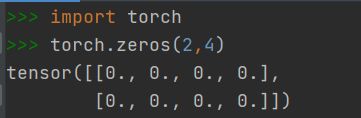
2.1.2 快速创建方法：torch.zeros()

• 创建元素全为0 的Tensor
  

2.1.3 快速创建方法：torch.eyes()

• 创建对角线位置的元素全为1，其他位置为0的Tensor
  

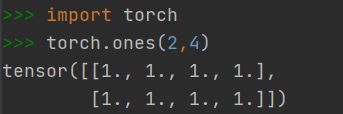
2.1.4 快速创建方法：torch.ones()

• 创建元素全为1的Tensor
  

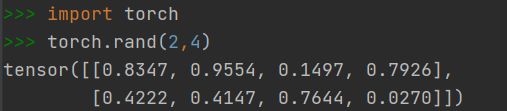
2.1.5 快速创建方法：torch.rand()

• 创建元素区间为[0,1]的随机数Tensor
  

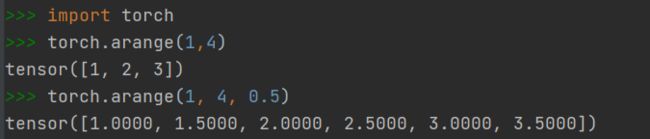
2.1.6 快速创建方法：torch.arange()

• 创建一个在区间内按指定步长递增的一维Tensor
• 前两个参数指定区间范围，左闭右开
• 第三个参数指定步长，默认为1

2.1.7 快速创建方法：torch.randn()

• 创建服从标准正态分布的一组随机数Tensor
  
  关于PyTorch的操作函数，以后再说，等我们用到什么百度什么就好了！

2.2 Autograd的基本原理

Autograd中文：自动微分，是PyTorch进行神经网络优化的核心。自动微分，就是PyTorch自动为我们计算微分。

1. Tensor在自动微分方面有3个重要属性：requires_grad，grad、grad_fn。
2. requires_grad属性是一个布尔值，默认为False。当设置为True时，表示该Tensor需要自动微分。
3. grad属性用于存储Tensor的微分值。
4. grad_fn属性用于存储Tensor的微分函数。

注意下面几点：

• 当叶子结点的requires_grad=True时，信息流经过该结点时，所有中间结点的requreis_grad都会=True。
• 在输出结点调用反向传播函数：backward()，PyTorch就会自动求出叶子结点的微分值，并更新存储到叶子结点的grad属性中。

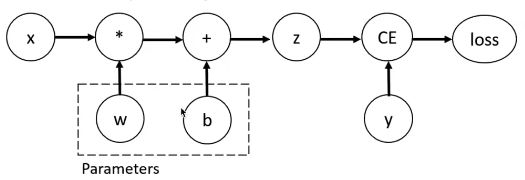
2.2.1 举个例子

• 比如说一个$y+w\ast x+b$的线性模型：

• 下面是这个计算过程的计算图：
  

• 其中，z是预测输出（计算输出），y是实际输出。loss函数就是用来计算这两个输出之间的差距大小，loss越小，模型预测效果越好！

• 下面代码可以直接运行！

import torch


x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

wimport torch


x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

w = torch.Tensor([1.0])
w.requires_grad = True


def forward(x):
    return w * x


def loss(x, y):  # 这里采用MSE均方差计算损失值
    y_pred = forward(x)
    return (y_pred - y) ** 2


print("在模型计算之前对于x=4的预测是：", 4, forward(4).item, '\n\n')


for epoch in range(20):
    for x, y in zip(x_data, y_data):
        l = loss(x, y)
        l.backward()
        print('\tgrad:', x, y, w.grad.item())
        w.data = w.data - 0.01 * w.grad.data

        w.grad.data.zero_()

    print("process:", epoch, l.item(), '\n')

print("在模型计算之后对于x=4的预测是：", 4, forward(4).item())
 = torch.Tensor([1.0])
w.requires_grad = True


def forward(x):
    return w * x


def loss(x, y):  # 这里采用MSE均方差计算损失值
    y_pred = forward(x)
    return (y_pred - y) ** 2


print("在模型计算之前对于x=4的预测是：", 4, forward(4).item, '\n\n')


for epoch in range(20):
    for x, y in zip(x_data, y_data):
        l = loss(x, y)
        l.backward()
        print('\tgrad:', x, y, w.grad.item())
        w.data = w.data - 0.01 * w.grad.data

        w.grad.data.zero_()

    print("process:", epoch, l.item(), '\n')

print("在模型计算之后对于x=4的预测是：", 4, forward(4).item())

如果这篇文章对你有帮助的话，谢谢点赞收藏关注啦啦啦！

3 线性回归

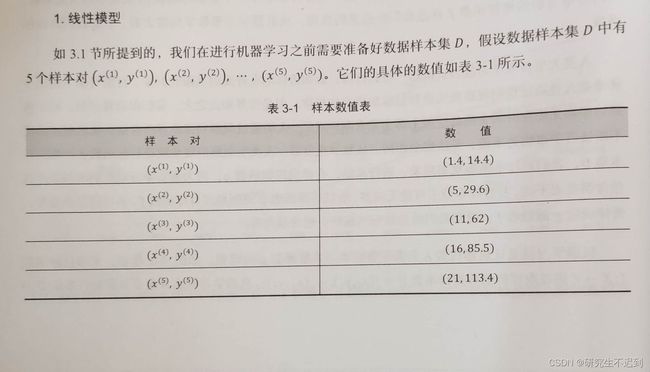
3.1 用scatter()方法绘制散点图【数据处理】

• 根据5条样本数据，对x和y画出散点图。
• 需要在注意的是，在使用matplotlib绘制图形时，传入的Tensor数据必须先转换为Numpy数据。

import torch
import matplotlib.pyplot as plt

x = torch.Tensor([1.4, 5, 11, 16, 21])
y = torch.Tensor([14.4, 29.6, 62, 85.5, 113.4])

plt.scatter(x.numpy(), y.numpy())
plt.show()

样本分布情况如下图所示，可以看出这里的数据符合线性规律，所以我们可以用线性模型去拟合它！

3.2 设置目标函数

$$y\_pred=w_{1}x+w_0$$

3.3 计算预测值y与真实值y之间的误差

• 我们用一个函数去衡量$y\_pred$与$y$之间的误差，这个函数有很多名字，例如损失函数、准则、目标函数、代价函数或者是误差函数。

• 这里采用的是$MSE$（均方误差），我们可以用Loss表示。

• MSE是关于$y\_pred$与$y$的函数，$y\_pred$是关于$w_1$和$w_0$的函数，也就是说Loss是关于$w_1$和$w_0$的函数。

• 模型训练的目标，就是不断修改$w_1$和$w_0$的值，让loss的误差最小。

3.4 优化

• 为了让损失函数L的值降到最小，我们需要调整$w_1$和$w_0$的值。

• 这里采用梯度下降的方法。梯度就是整个函数增长最快的方向，我们只要沿着这个梯度的反方向移动，理想上就能到达Loss的最低点。（然而现实中的数据都是存在一定噪声的，一般来说Loss是不为0的）

• 参数的更新：

$$w^{t+1}=w^t-\frac{dLoss}{d{w}^t}\times \alpha$$

• 这里α是学习率，大于0。学习率越大，下降的速度就越快。

3.5 流程图

3.6 代码实践

3.6.1 数据处理

• 五条数据信息如下：
  

def Produce_X(x):
    x0 = torch.ones(x.numpy().size)
    X = torch.stack((x, x0), dim=1)
    return X


x = torch.Tensor([1.4, 5, 11, 16, 21])
X = Produce_X(x)
y = torch.Tensor([14.4, 29.6, 62, 85.5, 113.4])

3.6.2 torch.stack()

• torch.stack((A1, A2), dim=0)：表示将A1和A2按行堆叠
• torch.stack((A1, A2), dim=1)：表示将A1和A2按列堆叠
  

3.6.3 训练数据

• 注意：更新完w之后，一定要清空w和grad的值，否则grad值会持续累加，这里使用zero_()函数来清空梯度！

def train(epochs=1, learning_rate=0.01):
    for epoch in range(epochs):
        output = inputs.mv(w)  # .mv()是矩阵与向量相乘
        loss = (output - target).pow(2).sum()  # .sum()返回Tensor的所有元素之和

        loss.backward()
        w.data -= learning_rate * w.grad
        w.grad.zero_()
        if epoch % 80 == 0:  # 每80次做一个输出
            draw(output, loss)
    return w,loss

3.6.4 Tensor.mv()

• 函数作用：矩阵与向量相乘

3.6.5 完整代码

• 这段代码可以直接运行！
• 觉得这篇文章对你有帮助的话，谢谢点赞收藏关注我哟！

import torch
import matplotlib.pyplot as plt


def Produce_X(x):
    x0 = torch.ones(x.numpy().size)
    X = torch.stack((x, x0), dim=1)
    return X


x = torch.Tensor([1.4, 5, 11, 16, 21])
X = Produce_X(x)
y = torch.Tensor([14.4, 29.6, 62, 85.5, 113.4])

inputs = X
target = y
w = torch.rand(2, requires_grad=True)


def draw(output, loss):
    plt.cla()
    plt.scatter(x.numpy(), y.numpy())
    plt.plot(x.numpy(), output.data.numpy(), 'r-', lw=5)
    plt.text(0.5, 0, 'loss=%s' % (loss.item()), fontdict={'size':20, 'color':'red'})

    plt.show()
    plt.pause(0.005)


def train(epochs=1, learning_rate=0.01):
    for epoch in range(epochs):
        output = inputs.mv(w)  # .mv()是矩阵与向量相乘
        loss = (output - target).pow(2).sum()  # .sum()返回Tensor的所有元素之和

        loss.backward()
        w.data -= learning_rate * w.grad
        w.grad.zero_()
        if epoch % 80 == 0:
            draw(output, loss)
    return w,loss


w, loss = train(1000, learning_rate=1e-4)
print("final loss:", loss.item())
print("weights:", w.data)

• 这是我epoches=100的输出结果：