图像的稀疏表示（Sparse Representation）

前言

在进入正题前先结合自己的经验对稀疏理论的相关内容扯几句。自己的话本身之前做了一段时间的图像融合内容，后来这块也放了放。但是之前在看论文的时候，基于稀疏理论的图像融合相关的论文还挺多的，但是一直没去仔细看这个，也没系统的整理过。最近看到好几篇2020年的论文，都是用这个做的融合，当然稀疏理论的应用场景远不止此。于是还是想再好好查一查，梳理一下。其实之前刚开始看这个东西的时候，挺抽象的，包括什么稀疏编码、字典学习等等，看着还挺吓人的。

因此在这里总结一下自己的学习过程，希望给每位学习图像稀疏表示的同学一点帮助。当然限于个人水平，很多内容我也不一定能说的特别清楚，尽量通过通俗清晰的方式说明。本文的主旨并不在于严密的数学论证和公式推导，更多的是帮助理解稀疏理论，整合一些或许有启发的思想，更详细的算法等已经有很多人整理的很好了。

其实网上相关的博文已经很多了，如果有一定的了解应该就明白，稀释表示里面最核心的两个任务：

1. 稀疏分解
2. 字典生成

由此衍生出来的，为了完成这两个任务的相关算法。但是其实，对于一个刚接触这个理论的人，一下子就直接就看这些内容，看了一圈可能还是对稀疏的概念不那么清晰。因此，建议刚开始学习稀疏表示的朋友按以下过程循序渐进，充分理解稀疏表示再进一步去看后续的算法，应该能对大家的学习有事半功倍的效果。

1. 稀疏信号
2. 稀疏表示
3. 稀疏分解
4. 字典生成
5. 应用

接下来，我会根据以上思路，根据我的理解结合网上的许多相关博文和相关论文，尽可能把这个问题讲的通俗一点。许多博文都写的很好，对我的学习也有很大的启发，我会尽量引用上，如有疏漏的，可以留言提醒。

那正式开始之前，对于一些喜欢看视频学习的或者想要系统过一遍的同学，在这里放上一个Duke大学的公开课视频链接，以及B站搬运的中文字幕版，但是这个翻译的很抽象，视频下方有YouTube的视频地址。

Duke大学公开课

bilibili搬运

稀疏信号

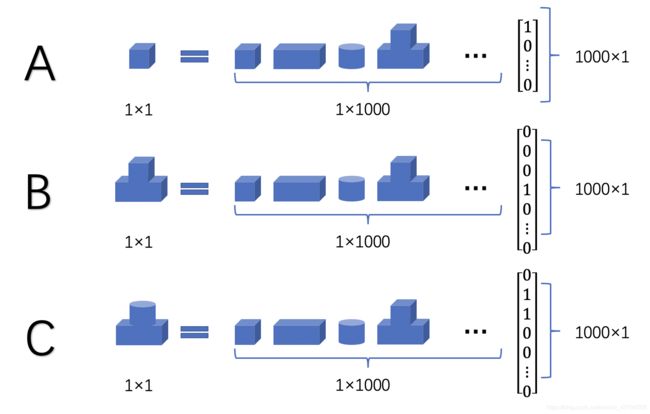
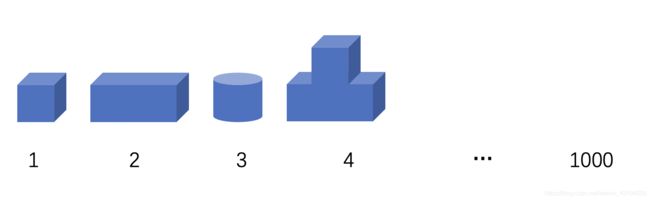
信号本身就是一个很广义的概念，图像、语音、文本、光、电等等都可以是信号。那在数学层面上，信号可以认为是一组反映原始信号特征的数据。将一个一维信号记为一个长度为N的向量，假设只有K个元素为非零的，其中K<

但是即便放宽稀疏性条件，现实中信号本身也都基本不满足稀疏性。例如，一副灰度图像可以认为是二维信号，但是如果该图像足够稀疏，也就是说大部分像素值都是0，那基本就是黑色的一片，而大部分情况下的图像都不是这样的。但是经过研究，一般的自然信号都可以通过一定的变换，在其变换域上呈现稀疏性，对这样的信号，一般认为是可稀疏的或者可压缩的，也即自然信号的稀疏性，以上先验也是信号稀疏表示的基础。

自然信号和人工信号的概念参考自这里:

信息与信号

信号变换的过程就是信号的稀疏表示过程，一个信号在一组过完备字典（基）上进行稀疏分解，在该字典上用尽可能少的原子来表示原始信号，由此得到一个稀疏向量，称这个稀疏向量是信号在这组基上的稀疏表示。

稀疏表示

上图为信号的稀疏表示模型，用数学公式可以描述为$X=D\alpha$，其中设$X\in R^N$为单一原始信号，$D\in R^{N\times K}$为过完备字典，$\alpha \in R^K$为稀疏表示结果。对于字典的每一列元素，称为原子(Atom)，记为$d_i\in R^{N}i=1,2,...,K$，进一步，为了让该式的$\alpha$满足稀疏性，我们加上$L_0$范数的稀疏性约束，最终得到以下公式：

$$X=\sum _{i=1}^K{d}_i\alpha =D\alpha \text{s.t.}\min ||\alpha |{|}_0\text{\hspace{1em}(1)}$$

说说稀疏模型也就这么回事，但是刚看到的朋友可能总感觉这个过程很抽象，也不清楚在干啥，或者说为什么这样这样做。什么字典啊，原子啊，过完备啊，到底是一个什么样的概念。那我在这里结合我的理解，一定程度上简化上面的过程，用更形象的图解要阐述瞎扯这个问题。

我本人并非一个LEGO爱好者，但是我最近想着，稀疏分解大概也就是搭积木、拆积木这么一回事。结合上面的数学公式，我从最简单的模型一步步向实际问题推进。

为了让问题显得更加简单，我们现在假设信号都是1维的，即每一个给定的乐高模型和每一块积木都对应于1个原子。据百度百科，LEGO现在大概有1300多种形状的积木，简单一点就假设一本LEGO字典$D_{1\times 1000}$有1000个原子，包含了所有可能的LEGO积木形状。

那一般来说，这个字典$D$都是过完备的，或者说是冗余的，具体的解释大家可以参考网上的回答，如什么是过完备字典？，简单的说就是所有原子之间并非线性无关，而是存在可以相互表示的情况，而在稀疏表示里面，这个字典的冗余度还比较高。而LEGO零件库也显然符合这个特征，下图是假设的包含1000个原子的字典局部示意图。

可以明显的感受到2号原子可以由2个1号原子来表示，4号原子可以有1个1号原子加1个2号原子，或者直接由3个1号原子来表示，这就说明了所有原子并非正交的，而是冗余的，而这种冗余性是稀疏表示所必要的。为什么必要，我们继续看下面的例子，我们用上面的字典分别去表示以下几个简单信号，我们的原始信号恰好是字典中的原子。

请看上图中A、B、C三种信号的稀疏分解结果。

A信号在字典中恰好等于1号原子，对A信号在D上进行稀疏分解，我们可以得到稀疏表示的结果$\alpha =[10...0{]}^T$，这是显然的且该结果是唯一的，$\alpha$也满足稀疏性，信号A被我们分解为了一个1000维的稀疏向量，稀疏度为1。

B信号相对于A信号相对复杂了，同时$\alpha$的解不是唯一的，正如我们之前说的，B可以由原子1、2、4不同的线性组合得到。但是别忘了我们还有稀疏度的约束条件，$\min ||\alpha |{|}_0$，稀疏度要越小越好，最终我们得到的稀疏解为$\alpha =[00010...0]$，稀疏度仍然为1。很好，我们的原始信号变复杂了，但是基于当前的字典D，他们的稀疏表示却没有变得复杂。这也解释了为什么我们要建立一个过完备字典，正是为了简化模型的复杂度，更好的表现信号的特征，同时我们保留了原始信号一个完整的特征，而不是把它拆成一些碎片的特征。这是冗余字典的优势，也即是稀疏表示的优势。

C信号的稀疏分解结果也就没什么好说了，我们很自然的可以得到一个稀疏度为2的解。但是同样的，除了图中的解，我们还有一个同样稀疏度为2的解${\alpha }_2=[2010...0]$，虽然是同样的稀疏度，但是我们还是选择了图中的解。正如B信号分解中所说的，冗余字典是为了尽可能保存原始信号的完整特征，图中的解系数均为1，复杂度更低，这种思想在之后稀疏分解的算法中也都有体现，如MP和OMP算法，都是基于贪婪算法，每次迭代寻找内积最大的原子。

---

看到这里，大家应该对信号稀疏分解有了更清晰的认识，甚至感觉有点简单？

不过很残念的是，现实中，无论是信号还是字典一般都没有那么规规矩矩，描述一个信号的稀疏解也往往没有那么简单，因此在实际寻找稀疏分解算法的时候仍有很多问题。我们继续基于上述假设的LEGO字典探究这个问题，假设原始信号如下图所示。

注：模型图片来源https://m.qctt.cn/news/192058

这下原始信号的复杂度大大提高，但是基于上述字典，假设我们利用任意一种追踪算法计算出了$\alpha$，且$\alpha$是K稀疏的，K<<1000。显然我们没法用以上字典原子的稀疏组合拼出一辆一毛一样的迈凯伦，根据计算得到的$\alpha$和$D$，我们可以重建信号。假设原始信号为$Y$，重建的信号为$Y^{{}^{\prime }}=D\alpha$，就得到了以下结果：

显然，实际情况大多数是这样的，由于解的稀疏性约束，我们往往尽可能获得一个逼近的近似结果（还是不得不说一句牛逼）。基于以上结果，记残差为$z$，可以得$Y=Y^{{}^{\prime }}+z=D\alpha +z$。

---

现在我们的模型已经接近实际问题了，只不过实际信号一般维度会更高，但是从字典中每一列表示一个原子的角度来讲已经足以说明问题了。当然，还有更实际的情况是，我们的原始信号往往还包含噪声，这部分暂时先不提，放在应用图像去噪中说明。

能够看到这里，并且理解上面的例子，大家应该明白稀疏表示是怎么一回事了，不过是将原始信号在某一组字典基上分解变换，得到另一个稀疏的表示而已。

讲到这里，我们终于回到了当前稀疏表示领域下的两个核心问题，稀疏分解方法和字典生成。

1. 在之前的乐高积木例子中，或是因为分解情况简单可以直接看出，或是假设我们可以分解，而未给出一种实际可行通用的算法。
2. 同时，我们的字典固定为乐高当前所有的积木类型，这是可行的，因为乐高积木的种类确实有限，也符合过完备字典的要求。

因此，当前稀疏表示领域中，以上两个任务是大家比较关心的，也是研究热点。当然，文章开头也说了，本文对这两块的算法不会具体展开讲，而是系统的概括和整理，更为详细的算法和流程网上已有许多很好的文章来说明，这里也会给出几个我参考的博客。

稀疏分解

在上一部分中提到，优化目标为：

$$X=\sum _{i=1}^K{d}_i\alpha =D\alpha \text{s.t.}\min ||\alpha |{|}_0\text{\hspace{1em}(1)}$$

上式也等同于

$$\min ||\alpha |{|}_0\text{s.t.}X=D\alpha \text{\hspace{1em}(2)}$$

在某种条件下，$L_0$范数的优化问题有唯一解，但是该问题依旧是NP难的，但是后来进一步证明了，在RIP条件下，0范数的优化问题与$L_1$范数的优化问题有相同的解，即满足下式：

$$\min ||\alpha |{|}_1\text{s.t.}X=D\alpha \text{\hspace{1em}(3)}$$

该理论可以参考：

Sparse Representation

压缩感知测量矩阵之有限等距性质

进一步的，考虑到原始信号的噪声，该问题还可以表示为以下公式：

$$\min ||\alpha |{|}_0\text{s.t.}||X-D\alpha |{|}_2^2\le ϵ\text{\hspace{1em}(4)}$$

总之，不管是什么形式，目前解决这个问题主要有以下两类：

1. 在$L_0$范数上直接优化的贪婪算法：MP，OMP以及各种改进的匹配追踪算法等
2. 在$L_p$范数上作为凸优化来求解：BP等

大佬压缩感知的专栏，内容很丰富

稀疏分解中的MP与OMP算法

字典生成

回到之前的例子，针对一个给定的原始信号（物体），我们的LEGO字典似乎总能求得一个近似的稀疏解。那在实际的信号处理中，是否存在一类字典，可以广泛用于各类信号的稀疏分解中，答案是肯定的。很多研究都基于某个数学模型来构造字典，常见的比如DCT变换，小波变换，gabor变换等。

以DCT（离散余弦变换）为例，DCT字典本身是一个用于余弦变换时所采用的变换矩阵，但是它本身是一个正交字典（方阵），它是个完备字典，却不是过完备字典。但是通过对字典中的原子进行一定的操作可以调制出一个过完备字典，具体方法可以参考：

构建DCT过完备字典

但是说到底，无论我们的LEGO字典还是以上提到的过完备字典，其表达能力终究是有限的，远不能满足自然界中各种信号的复杂性和多样性。其在遇到某种表达能力之外的信号时，提取特征的能力就会大大下降。以LEGO为例，面对许多光滑曲面的物体，LEGO字典总是无法很好的描述这样的特征，从而导致重建的结果出现残差，究其原因还是其零件库里就缺少具备这类特征的积木，这在信号的稀疏分解过程中也是一样。

所以为了解决这个问题，提出了不少针对原始信号自适应的字典学习方法。

其中比较的著名的如K-SVD算法，其思想上相当于K-means的一种推广和拓展，迭代交替更新字典中的原子和稀疏解，最终算法收敛的时候就生成了自适应字典以及对应的稀疏系数。与K-means类似的是，算法需要指定迭代次数或者收敛误差。具体实现可以参考：

原文 K-SVD: An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation - 2006

字典学习（Dictionary Learning, KSVD）详解

应用

其实，稀疏表示还是算比较新的理论，近些年也还有很多包括理论和应用的论文。但是深度学习目前在各个领域展现出的优秀性能，其他各类理论都被统一成了传统算法，以及稀疏表示自身的一些问题，导致在有些应用上表现显得不够突出。

但是不管怎么说，在许多问题的求解上，稀疏表示还是很有价值的，这里简单说一下应用，之后有时间或者有感的话会结合具体的论文写一下方法什么的。

图像稀疏表示

之前讲来讲去都是信号，所以图像到底怎么进行稀疏表示。假设图像的大小为$M\times N$，直接把整个图像拉成一个一维信号显然是不合适的，我们看看这个优化问题的大小，信号大小为$MN\times 1$，由于字典的冗余特性，字典大小至少为，$MN\times kMN$这里k表示一个冗余系数，即过完备的程度，k越大，字典约冗余，字典的大小也到了一个夸张的地步。一方面计算效率低，一方面不能很好描述局部特征，所以一般都是在图像上用滑动窗口取一个Patch，一般是8×8的窗口。

具体方法在下面图像去噪论文中有提到。例如一个大小为20×20的图像，以8×8的窗口和1的步长滑动，将图像分成列向量信号表示，每一次窗口可以提取64维列向量，一次遍历可以得到$(20-8+1{)}^2=169$个列向量，假设冗余系数k取4，即需要计算169个稀疏解$Y^{64\times 169}=D^{64\times 256}{\alpha }^{256\times 169}$。

然后重构图像，并将对应的结果还原回图像中，即可得的稀疏表示后的图像。

图像去噪

Image Denoising Via Sparse and Redundant Representations Over Learned Dictionaries

与K-SVD算法一起，同一个作者在同年发表了一个去噪论文。传统上基于滤波的图像去噪方法，假设噪声总是高频信息，然后基于一定的局部约束进行去噪。而稀疏表示去噪的理论基于，自然图像信号总是可以稀疏表示的，而噪声是无法稀疏表示的，假设含噪图像（观测图像）为$Y$，其噪声模型满足以下公式：

$$Y=D\alpha +noise\text{\hspace{1em}(5)}$$

则$noise$即为图像噪声，$D\alpha$重构结果即是去噪图像。实际中，图像往往受到多种类型的噪声的影响，根据中心极限定理，多个独立同分布的噪声叠加趋近于正态分布，因此我们可以用高斯噪声模型先验来给定$noise$的误差阈值，控制稀疏分解停止的条件，对$Y$进行稀疏表示后再重建，即可得到去噪结果。

那说到为啥噪声一般不能进行稀疏表示，之前看到的一个类比的说法是，例如，对于任一大小n×m的8bit图像，在每个像素点上的可能性有256级灰度，因此整个图像的所有可能情况为$256^{mn}$，而实际的自然图像信号往往只涵盖了其中很小一部分，而这部分往往是可稀疏的，即可压缩的，这算是长期以来的经验性知识，比如最经典的jpeg图像压缩算法的泛用性已经证明了这一点。

该论文在网上有Matlab版的K-SVD以及图像去噪的Demo可获取，很适合学习，大家应该搜一下就可以搜到，之后有空会做一个去噪的笔记，也会贴一个中文注释后的代码帮助理解。

更多改进的论文这里就不提了。

图像融合

在网上其实很少看到稀疏表示用于图像融合领域的博客什么，但是文章开头也说了，我自己在图像融合领域有一定的浸淫，所以会相对关注一些。最早把稀疏理论用于图像融合是湖南大学的李树涛教授，其在稀疏表示，图像融合，模式识别等领域研究水平都相当高，很多论文的引用都很高，这是教授的简介：

人物和研究简介

最早的一篇稀疏表示用于像素级图像融合的论文为

Pixel-level Image Fusion with Simultaneous Orthogonal Matching Pursuit - 2012

该文提出了一种对多源图像在同一个字典上进行稀疏分解的算法，SOMP（Simultaneous Orthogonal Matching Pursuit）即同时正交匹配追踪，对多幅图像相同位置计算出的稀疏系数取绝对值较大值，得到融合后的稀疏系数，然后结合字典进行重建得到融合后的图像。

以及我曾写过的一篇基于引导滤波的图像融合笔记也是他的一作论文

Image Fusion with Guided Filtering - 2013

在这里不作更多展开的介绍了，之后有空会稍微整理一下利用稀疏理论进行图像融合的思路。啊啊啊，什么都是等有空再做，疯狂挖坑，简直无情，危

图像重构

压缩感知，图像修复，图像超分辨率重建（SR，CSR卷积稀疏表示等，感觉效果挺好的，之后有空再补，继续挖坑）

等等等等等。

目标跟踪

人脸识别

后面两个没怎么研究过，也不熟，大家有兴趣自己去探索。

其他

文章可能还不完善，还有很多点没有详细展开，之后看自己是否有时间和需求再行补充。

这里再放一个稀疏工具包，用C++编写的，可以达到很高的性能，同时提供了Matlab和Python的接口，有兴趣的朋友可以自己去试试。

SPAMS

如果本文对你有帮助，不妨点个赞加个收藏。

文章中有任何问题和错误，欢迎留言。