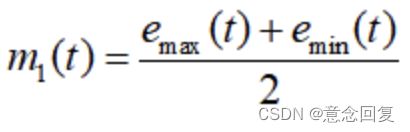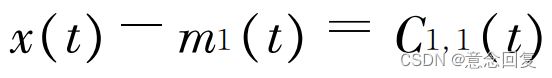经验模态分解（EMD）

1 背景

        实际工程测量中由于测量系统受外界环境影响经常在测量信号中产生趋势项。趋势项是指信号中周期大于采样长度的频率成分，通常表现为线性的或者慢变的趋势误差。提取和消除信号中存在的趋势项是信号预处理的一个重要环节，趋势项会严重影响信号时域相关分析和频域功率谱估计精度，严重的趋势项干扰会使低频谱严重失真。

        目前提取趋势项的方法主要有：平均斜率法、差分法、低通滤波法和最小二乘拟合法等。这些方法通常需要预先明确信号中趋势项的类型，如线性趋势项、多项式或指数趋势项等，不适用于复杂变化的趋势项提取，很大程度上限制了其应用范围。

         近年来已有利用 EMD 进行趋势项提取的研究成果报道。利用 EMD 进行趋势项提取可不考虑趋势项的类型，具有自适应性因此适用范围更广泛。但是利用EMD 进行趋势项提取有一个不可忽视的前提条件：就是测试信号必须能够完全分解，即满足可分解条件，否则会导致模态混叠。此时趋势项很可能会同时存在于分解余量和低频 IMF 分量中，这种情况下利用 EMD 进行趋势项提取则会遇到困难。而影响 EMD 分解性能的另外一个因素：端点效应同样会波及到分解余量中，导致趋势项提取不够精确。

        EMD最显著的特点，就是其克服了基函数无自适应性的问题。啥意思呢？回忆小波分析部分的内容，我们会知道小波分析是需要选定某一个小波基的，小波基的选择对整个小波分析的结果影响很大，一旦确定了小波基，在整个分析过程中将无法更换，即使该小波基在全局可能是最佳的，但在某些局部可能并不是，所以小波分析的基函数缺乏适应性。

        通俗的说，用EMD有什么好处呢？对于一段未知信号，不需要做预先分析与研究，就可以直接开始分解。这个方法会自动按照一些固模式按层次分好，而不需要人为设置和干预。

        再通俗一点，EMD就像一台机器，把一堆混在一起的硬币扔进去，他会自动按照1元、5毛、1毛、5分、1分地分成几份。

2 时间序列平稳性

         所谓时间序列的平稳性，一般指宽平稳，即时间序列的均值和方差为与时间无关的常数，其协方差与时间间隔有关而也与时间无关。简单地说，就是一个平稳的时间序列指的是：遥想未来所能获得的样本时间序列，我们能断定其均值、方差、协方差必定与眼下已获得的样本时间序列等同。 
        反之，如果样本时间序列的本质特征只存在于所发生的当期，并不会延续到未来，亦即样本时间序列的均值、方差、协方差非常数，则这样一个时间序列不足以昭示未来，我们便称这样的样本时间序列是非平稳的。 
        形象地理解，平稳性就是要求经由样本时间序列所得到的拟合曲线在未来的一段时间内仍能顺着现有的形态“惯性”地延续下去；如果数据非平稳，则说明样本拟合曲线的形态不具有“惯性”延续的特点，也就是基于未来将要获得的样本时间序列所拟合出来的曲线将迥异于当前的样本拟合曲线。 
        事实上，世界上几乎不存在理想的“平稳”时间序列。欧阳首承教授曾指出：“平稳序列性消除了小概率事件”。即在欧阳教授的溃变论看来，EMD这一方法也是有问题的。但是，该方法确实扩展了平稳化这一传统思想的应用范围，即扩展到了对任何类型的时间序列的处理，也是了不起的新进展。

3 EMD 方法

         EMD 方法是美国 NASA 的黄锷博士提出的一种针对非平稳信号的分析方法。EMD 过程实质上是对非平稳信号进行平稳化处理的一种手段。其结果是将信号中不同尺度的波动和趋势进行逐级分解，产生一系列具有不同特征尺度的数据序列，每一个序列称为一个固有模态函数 IMF。

         每一个 IMF必须满足2个条件：

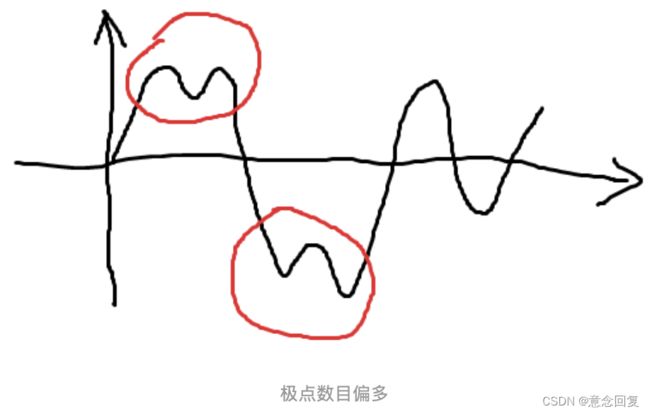
1. 在整个时程内极值点个数与过零点个数相等或最多相差1；
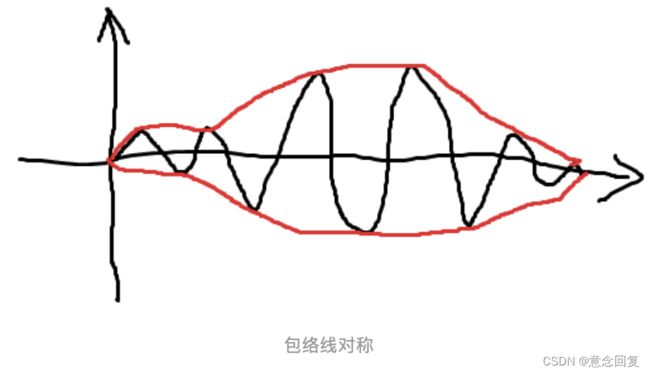
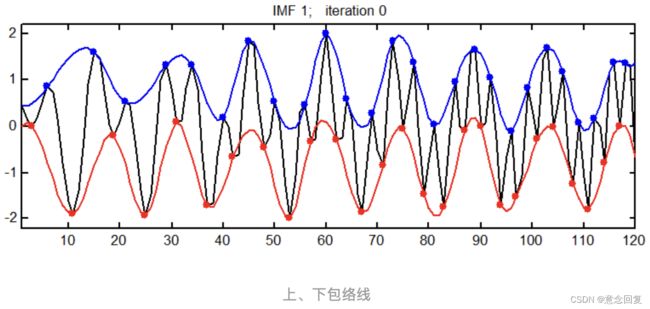
2. 在任意时刻，由局部极大值点形成的上包络线和由局部极小值点形成的下包络线的平均值为零，即上、下包络线相对于时间轴局部对称。

啥意思？

1）图线要反复跨越x轴，像这样：

       而不能像这样某次穿过零点后出现多个极点：

 2）包络线要对称，像这样：

而不能像这样：

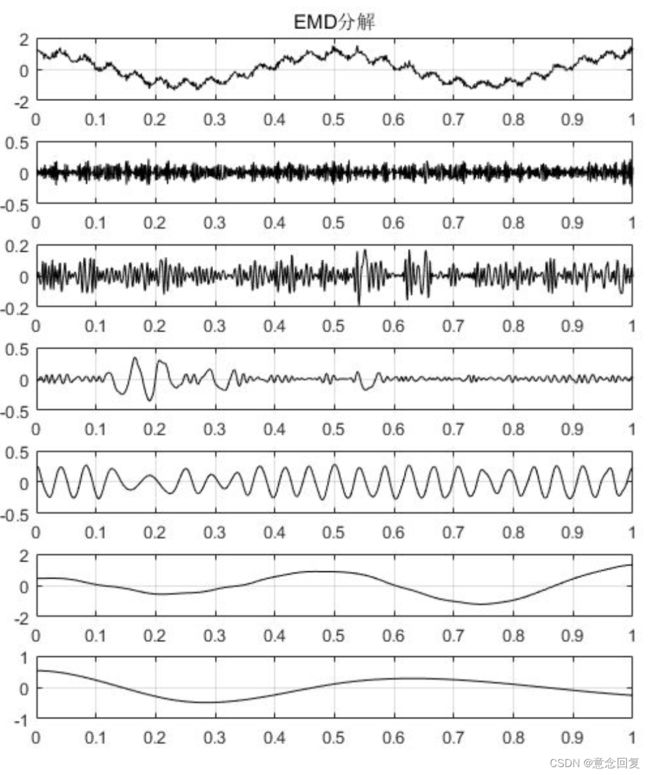
EMD分解示例：

 

         上图由7张图片组成，

• 其中第1张为原始信号，
• 后边依次为EMD分解之后得到的6个分量，分别叫做IMF1~IMF5，
• 最后一张图为残差，

        每一个IMF分量代表了原始信号中存在的一种内涵模态分量。可以看出，每个IMF分量都是满足这两个约束条件的。 

EMD方法中假设：

　　（1）任何信号都可以分解为若干个IMF分量；

　　（2）各个IMF分量可以是线性的或非线性的，局部的零点数和极值点数相同，且上下包络关于时间轴局部对称；

　　（3）一个信号可包含若干个IMF分量。

4 EMD 过程

        任何复杂的信号均可视为多个不同的固有模态函数叠加之和，任何模态函数可以是线性的或非线性的，并且任意两个模态之间都是相互独立的。在这个假设基础上，复杂信号x(t)的EMD分解步骤如下：

步骤1：

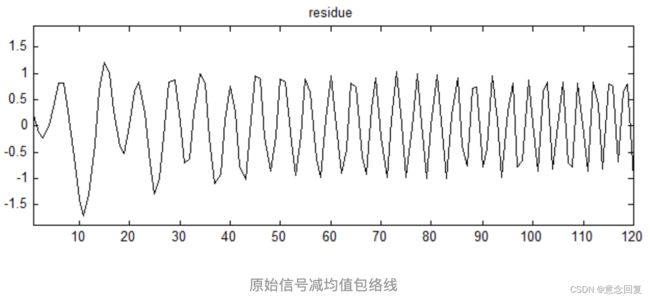
        寻找信号 全部极值点，通过三次样条曲线将局部极大值点连成上包络线，将局部极小值点连成下包络线。上、下包络线包含所有的数据点。

        

步骤2：

       由上包络和下包络线的平均值，得出

         

          

 步骤3：

         原始信号减均值包络线，得到中间信号。 

          

         这个过程称为“筛分”原始信号 x（t）经过一次“筛分”得到一个新的信号 。

         

 步骤4：

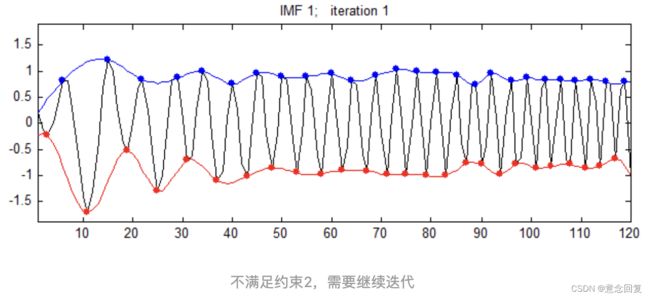
         判断该中间信号是否满足IMF的两个条件，如果满足，该信号就是一个IMF分量；如果不是，以该信号为基础，重新做1）~4）的分析。即继续进行“筛分”直至分解 k 次后分解得到的信号满足 IMF 条件得到原始信号的第一个 IMF 分量。

           

          代表原始信号 x（t）中最高频的 IMF 分量，从原始信号 x（t）中减去得到剩余分量 r1（t）。

        IMF分量的获取通常需要若干次的迭代。 

      

 步骤5：

        对 r1（t）进行上述“筛分”处理，可得到第二个 IMF 分量 I2（t），再将 r1（t）减去 I2（t）后获得剩余分量 r2（t）。如此分解下去，直到最后一个残余信号 rn（t）无法继续分解为止，完成对信号 x（t）的 EMD 过程：

         

 步骤6:

         当 变成单调函数后，剩余的 成为残余分量。所有IMF分量和残余分量之和为原始信号 x(t)：

          

         在 EMD 的“筛分”过程中可以看出与傅里叶变换和小波分解相比较EMD 不需要设定基函数因此适用范围更广泛。

        将原始信号 x（t）分解后第一个 IMF 分量包含原始信号 x（t）中时间尺度最小（频率最高）的成分随着 IMF 阶数的增加其对应的频率成分逐渐降低。其中余量的频率成分
最低。根据 EMD 分解收敛条件，分解余量 为单调函数，周期大于信号的记录长度，因此可以将作为趋势项。

 5 EMD 方法的缺陷

        EMD 方法适用信号范围广泛，不受信号和趋势项类型约束。但是利用 EMD方法有两个缺陷：

（1）提取趋势项必须要求原始信号本身满足可分解条件，即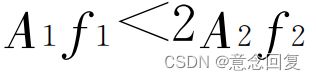，其中，代表多分量信号中分量1的幅度和频率，代表多分量信号中分量2的幅度和频率。如果可分解条件得不到满足，则会在 EMD 过程中产生模态混叠，导致不同频率成分共存于同一个 IMF 分量中。那么作为低频的趋势项成分，也可能会混叠在与之接近的低频IMF 分量中，此时用分解余量作为趋势项会使趋势项提取不完全。

（2）EMD 另外一个缺陷是端点效应问题。在 EMD 分解中关键的一个步骤是采用三次样条法求上下包络的平均值，三次样条曲线具有光滑的一次微分和连续的二次微分特点。由于所分析信号长度有限，信号的两端点不能确定是极值。因此在进行三次样条插值时，必然使信号的上下包络
在信号两端附近严重扭曲。在信号的高频分量中，由于时间尺度小，极值间的距离小，端部的边缘效应仅局限在信号两端很小的部分。但对于低频分量，时间尺度大，极值间的距离大，端部的边缘效应就传播到信号内部，特别是原始信号数据集比较短时，会严重影响 EMD 分解的质量 。作为分解余量 ，同样受到端点效应的影响，这种情况下简单地把 作为趋势项处理，同样会影响趋势项提取精度。

端点效应：

 

 6 Python 

pip install EMD-signal == 0.2.10

import numpy as np
from PyEMD import EMD, Visualisation
import matplotlib.pyplot as plt

# data = np.random.randint(6, 10, 300)
# 构建信号
# t = np.arange(0,1, 0.01)
t = np.linspace(0, 100, 100)
data = 2*np.sin(2*np.pi*15*t) +4*np.sin(2*np.pi*10*t)*np.sin(2*np.pi*t*0.1)+np.sin(2*np.pi*5*t) + 0.05 * t + 1

# t = np.linspace(0, 100, 100)
# data = 0.05 * t + 1

plt.plot(data)
plt.show()

emd = EMD()
emd.emd(data)
imfs, res = emd.get_imfs_and_residue()
imf = imfs.sum(axis=0) - imfs[-1]
print(imf)
plt.plot(imf)
plt.show()
# 趋势画图
plt.plot(imfs[-1])
plt.show()

# 绘制 IMF
vis = Visualisation()
vis.plot_imfs(imfs=imfs, residue=res, t=t, include_residue=True)
# 绘制并显示所有提供的IMF的瞬时频率
vis.plot_instant_freq(t, imfs=imfs)
vis.show()

 

改​​​​​​善EMD端点效应的方法 - 知乎

什么是EMD（经验模态分解）的端点效应？ - 知乎

EMD算法原理与python实现_脑机接口社区的博客-CSDN博客_emd python

二、信号分解 —＞经验模态分解（EMD）学习笔记_追逐者-桥的博客-CSDN博客_emd解决模态混叠用频率移动

 这篇文章能让你明白经验模态分解（EMD）——基础理论篇 - 知乎

有道云笔记