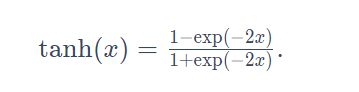深度学习+pytorch自学笔记（五）——MLP多层感知机

参考书籍《动手学深度学习(pytorch版），参考网址为：
https://zh-v2.d2l.ai/chapter_multilayer-perceptrons/index.html

https://tangshusen.me/Dive-into-DL-PyTorch/#/chapter03_DL-basics/3.8_mlp

请大家也多多支持这两个很好用的平台~

大部分内容为书中内容，也有部分自己实验和添加的内容，如涉及侵权，会进行删除。

一、基本概念和模型

1.隐藏层

多层感知机在单层神经网络的基础上引入了一到多个隐藏层（hidden layer）。隐藏层位于输入层和输出层之间。图3.3展示了一个多层感知机的神经网络图，它含有一个隐藏层，该层中有5个隐藏单元。

在图3.3所示的多层感知机中，输入和输出个数分别为4和3，中间的隐藏层中包含了5个隐藏单元（hidden unit）。由于输入层不涉及计算，图3.3中的多层感知机的层数为2。由图3.3可见，隐藏层中的神经元和输入层中各个输入完全连接，输出层中的神经元和隐藏层中的各个神经元也完全连接。因此，多层感知机中的隐藏层和输出层都是全连接层。

2.激活函数

上述问题的根源在于全连接层只是对数据做仿射变换（affine transformation），而多个仿射变换的叠加仍然是一个仿射变换。解决问题的一个方法是引入非线性变换，例如对隐藏变量使用按元素运算的非线性函数进行变换，然后再作为下一个全连接层的输入。这个非线性函数被称为激活函数（activation function）。下面我们介绍几个常用的激活函数。

2.1 ReLU函数

ReLU（rectified linear unit）函数提供了一个很简单的非线性变换。给定元素xx，该函数定义为

可以看出，ReLU函数只保留正数元素，并将负数元素清零。为了直观地观察这一非线性变换，我们先定义一个绘图函数xyplot。

显然，当输入为负数时，ReLU函数的导数为0；当输入为正数时，ReLU函数的导数为1。尽管输入为0时ReLU函数不可导，但是我们可以取此处的导数为0。下面绘制ReLU函数的导数。

2.2 sigmoid函数

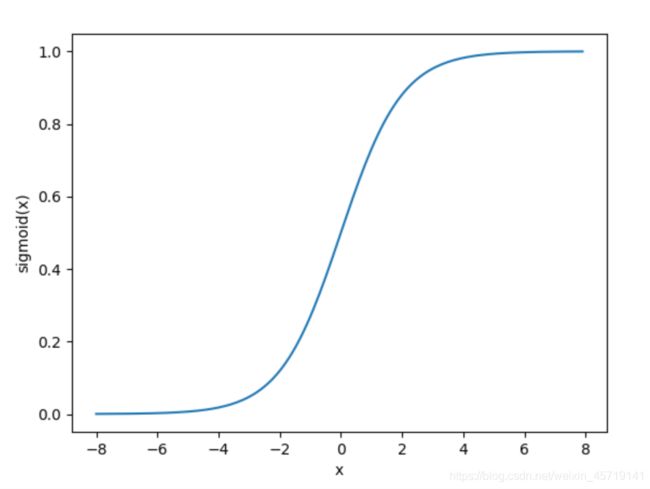
sigmoid函数可以将元素的值变换到0和1之间：

sigmoid函数在早期的神经网络中较为普遍，但它目前逐渐被更简单的ReLU函数取代。在后面“循环神经网络”一章中我们会介绍如何利用它值域在0到1之间这一特性来控制信息在神经网络中的流动。下面绘制了sigmoid函数。当输入接近0时，sigmoid函数接近线性变换。

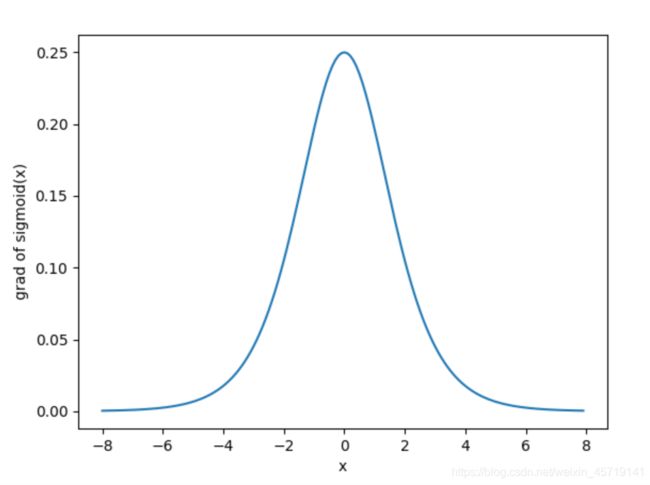
依据链式法则，sigmoid函数的导数

下面绘制了sigmoid函数的导数。当输入为0时，sigmoid函数的导数达到最大值0.25；当输入越偏离0时，sigmoid函数的导数越接近0。

2.3 tanh函数

tanh（双曲正切）函数可以将元素的值变换到-1和1之间：

我们接着绘制tanh函数。当输入接近0时，tanh函数接近线性变换。虽然该函数的形状和sigmoid函数的形状很像，但tanh函数在坐标系的原点上对称。

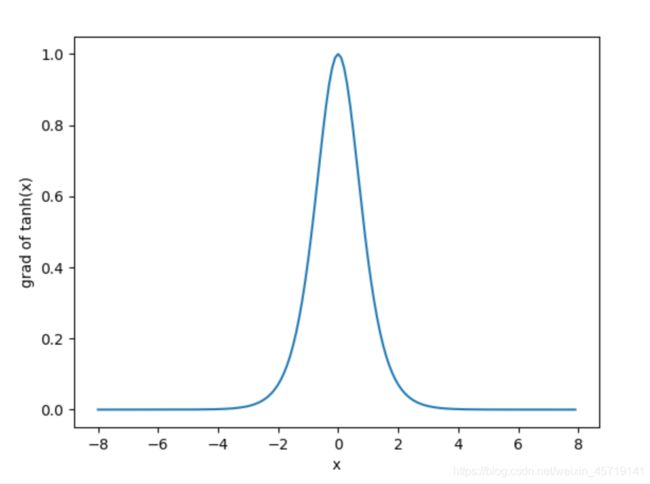
依据链式法则，tanh函数的导数

下面绘制了tanh函数的导数。当输入为0时，tanh函数的导数达到最大值1；当输入越偏离0时，tanh函数的导数越接近0。

2.4 代码

demo1:

import torch
import matplotlib.pylab as plt

def xyplot(x_vals, y_vals, name):
    #d2l.set_figsize(figsize=(5, 2.5))  #在PyCharm里运行，不画矢量图，SVG可伸缩矢量图形
    plt.plot(x_vals.detach().numpy(), y_vals.detach().numpy())  #detach()不需要梯度，防止被追踪
    plt.xlabel('x')
    plt.ylabel(name + '(x)')
    plt.show()

#ReLU函数
x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = x.relu()
xyplot(x, y, 'relu')

y.sum().backward()
xyplot(x, x.grad, 'grad of relu')

#sigmoid函数
y = x.sigmoid()
xyplot(x, y, 'sigmoid')

x.grad.zero_()
y.sum().backward() #把梯度清零
xyplot(x, x.grad, 'grad of sigmoid')

#tanh函数
y = x.tanh()
xyplot(x, y, 'tanh')

x.grad.zero_()
y.sum().backward()
xyplot(x, x.grad, 'grad of tanh')

out1:

3.总结

多层感知机就是含有至少一个隐藏层的由全连接层组成的神经网络，且每个隐藏层的输出通过激活函数进行变换。多层感知机的层数和各隐藏层中隐藏单元个数都是超参数。以单隐藏层为例并沿用本节之前定义的符号，多层感知机按以下方式计算输出：

其中ϕ表示激活函数。

二、多层感知机——从零开始实现

demo2:

import torch
import numpy as np
import d2lzh_pytorch as d2l
import myutils #导入自己改编后的train_ch3()函数和绘图函数

#获取和读取数据
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

#定义模型参数
num_inputs, num_outputs, num_hiddens = 784, 10, 256  #设超参数隐藏单元个数为256

W1 = torch.tensor(np.random.normal(0, 0.01, (num_inputs, num_hiddens)), dtype=torch.float)
b1 = torch.zeros(num_hiddens, dtype=torch.float)
W2 = torch.tensor(np.random.normal(0, 0.01, (num_hiddens, num_outputs)), dtype=torch.float)
b2 = torch.zeros(num_outputs, dtype=torch.float)

params = [W1, b1, W2, b2]
for param in params:
    param.requires_grad_(requires_grad=True)

#定义激活函数
def relu(X):
    return torch.max(input=X, other=torch.tensor(0.0))

#定义模型
def net(X):
    X = X.view((-1, num_inputs))
    H = relu(torch.matmul(X, W1) + b1)
    return torch.matmul(H, W2) + b2

#定义损失函数
loss = torch.nn.CrossEntropyLoss() #为了得到更好的数值稳定性，我们直接使用PyTorch提供的包括softmax运算和交叉熵损失计算的函数

#训练模型
#d2lzh_pytorch里面的sgd函数在更新的时候除以了batch_size，其实PyTorch在计算loss的时候已经除过一次了，sgd这里应该不用除了
num_epochs, lr = 5, 100.0
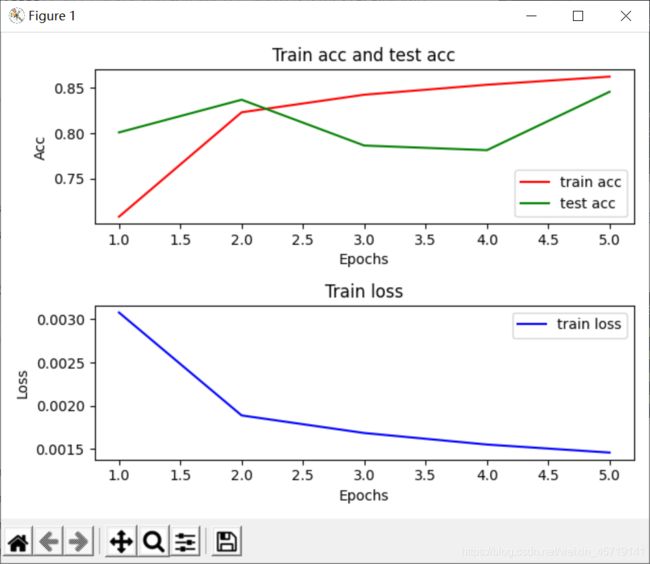
loss_list, train_acc_list, test_acc_list = myutils.train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, params, lr)
myutils.show_img(num_epochs, loss_list, train_acc_list, test_acc_list)

注：myutils包见深度学习+pytorch自学笔记（四）

out2:

epoch 1, loss 0.0031, train acc 0.708, test acc 0.801
epoch 2, loss 0.0019, train acc 0.823, test acc 0.837
epoch 3, loss 0.0017, train acc 0.843, test acc 0.786
epoch 4, loss 0.0016, train acc 0.854, test acc 0.781
epoch 5, loss 0.0015, train acc 0.863, test acc 0.846

三、多层感知机——简洁实现

demo3:

import torch
from torch import nn
import d2lzh_pytorch as d2l
import myutils #导入自己改编后的train_ch3()函数和绘图函数

net = nn.Sequential(nn.Flatten(), nn.Linear(784, 256), nn.ReLU(),
                    nn.Linear(256, 10))   ##设超参数隐藏单元个数为256

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

batch_size, lr, num_epochs = 256, 0.1, 10   #由于这里使用的是PyTorch的SGD而不是d2lzh_pytorch里面的sgd，所以就不存在学习率看起来很大的问题
loss = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(net.parameters(), lr=lr)

train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
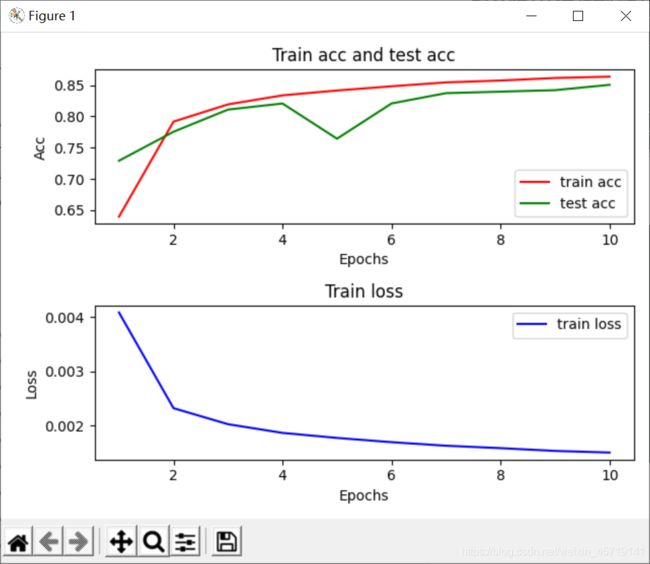
loss_list, train_acc_list, test_acc_list = myutils.train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, None, None, optimizer)
myutils.show_img(num_epochs, loss_list, train_acc_list, test_acc_list)

out3:

epoch 1, loss 0.0041, train acc 0.639, test acc 0.729
epoch 2, loss 0.0023, train acc 0.792, test acc 0.775
epoch 3, loss 0.0020, train acc 0.819, test acc 0.811
epoch 4, loss 0.0019, train acc 0.834, test acc 0.821
epoch 5, loss 0.0018, train acc 0.841, test acc 0.764
epoch 6, loss 0.0017, train acc 0.848, test acc 0.821
epoch 7, loss 0.0016, train acc 0.854, test acc 0.837
epoch 8, loss 0.0016, train acc 0.857, test acc 0.840
epoch 9, loss 0.0015, train acc 0.861, test acc 0.842
epoch 10, loss 0.0015, train acc 0.864, test acc 0.851