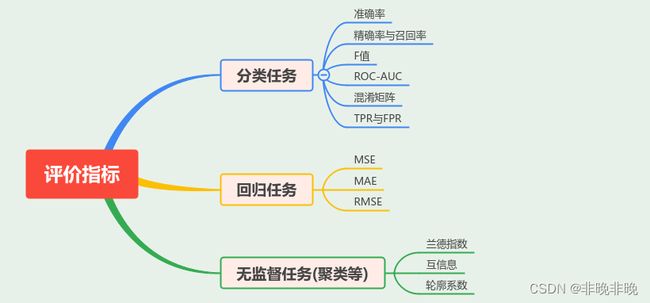
机器学习中常见的评价指标总结
文章目录
- 1. 评价指标的种类
- 2. 分类任务的评价指标
-
- 2.1 分类任务的一些概念
-
- (1) 交并率(IoU, Intersection over Union)
- (2)NMS
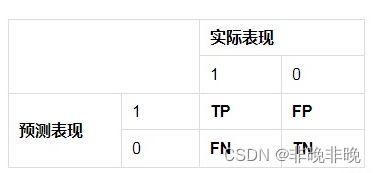
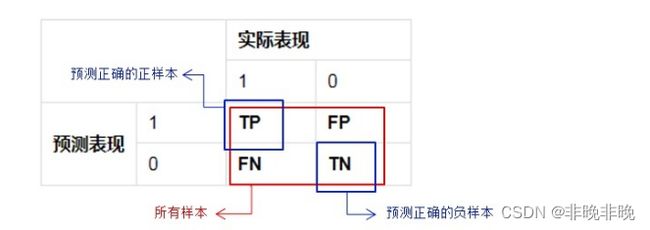
- (3)TP、FP、FN、TN与混淆矩阵
- 2.2 准确率(Accuracy)
- 2.3 精确率与召回率(Precision , Recall)
- 2.4 F1分数
- 2.5 G分数
- 2.6 AP和mAP
- 2.7 ROC与AUC
-
- (1)ROC
- (2)AUC
- 3. 回归任务的评价指标
-
- 3.1 MSE
- 3.2 MAE
- 3.3 RMSE
1. 评价指标的种类
评价指标是建立在不同的机器学习任务上的,主要分为三大类:分类、回归和无监督。
学习中遇到的分类任务中的评价指标有准确率(Accuracy)、TPR、FPR、Recall、Precision、F-score、MAP、ROC曲线和AUC等,回归任务中的指标有MSE、MAE等。
2. 分类任务的评价指标
2.1 分类任务的一些概念
![]()
如上图所示,绿颜色的为GT Box(ground truth box),红颜色的Predict Box。如果要正确检测出图中的猫和狗,那怎么才能算是正确的检测呢?下边的这三个标准都是需要看的:
- GT与预测框IoU是否大于阈值
- 预测的类别是否正确?
- 置信度是否大于阈值?
(1) 交并率(IoU, Intersection over Union)
IoU的作用是评价两个矩形框之间的相似性,在目标检测中是度量两个检测框的交叠程度,它的计算公式如下:
a r e a ( B g t ∩ B p ) a r e a ( B g t ∪ B p ) \frac{area(B_{gt}\cap B_p)}{area(B_{gt}\cup B_p)} area(Bgt∪Bp)area(Bgt∩Bp)
其中 B g t B_{gt} Bgt表示GT Box, B p {B_p} Bp表示Predict Box。IOU的计算图示如下。
![]()
一般来说,这个IOU> 0.5 就可以被认为一个不错的结果了。
(2)NMS
NMS即non maximum suppression,也就是非极大抑制,顾名思义就是抑制不是极大值的元素,搜索局部的极大值。
所谓非极大值抑制:先假设有6个 混淆矩阵(Confusion Matrix)又被称为错误矩阵,通过它可以直观地观察到算法的效果。它的每一列是样本的预测分类,每一行是样本的真实分类(反过来也可以),顾名思义,它反映了分类结果的混淆程度。 混淆矩阵形式如下。 下列Positive和Negative表示模型对样本预测的结果是正样本(正例)还是负样本(负例)。True和False表示预测的结果和真实结果是否相同。 准确率(Accuracy)衡量的是 精准率(Precision)又叫查准率,它是指被 召回率(Recall)又叫查全率,它是针对原样本而言的,它的含义是在实际为正的样本中被预测为正样本的概率,也就是 R e c a l l = 5 5 + 0 = 100 % Recall = \frac{5}{5+0}=100\% Recall=5+05=100% 有时候我们需要在精确率与召回率间进行权衡,一种选择是画出精确率-召回率曲线(Precision-Recall Curve),曲线下的面积被称为AP分数(Average precision score);另外一种选择是计算 F β F_β Fβ分数。 G分数是另一种统一精准率和召回率的系统性能评估标准。F分数是准确率和召回率的调和平均数,而G分数被定义为 G = p r e c i s i o n ∗ r e c a l l G = \sqrt{precision*recall} G=precision∗recall P-R曲线定义如下:根据学习器的预测结果(一般为一个实值或概率)对测试样本进行排序,将最可能是“正例”的样本排在前面,最不可能是“正例”的排在后面,按此顺序逐个把样本作为“正例”进行预测,每次计算出当前的P值和R值,如下图所示: 下面以3张图片为例,说明AP和mAP的计算过程: 该表中的顺序是按Confidence从高到低排序的, 加入第三张图片后,再加上前两张中的待检测目标,共有 n u m o b = 7 num_{ob}=7 numob=7个目标需要检测,检测情况如下表所示: 依次取Confidence的阈值为[0.98, 0.89, 0.88, 0.78, 0.66, 0.61, 0.52],计算对应的查准率和查全率如下表所示: 以Confidence thread=0.52为例,此时的TP=5,误检FP=2,第一张和第三张两张图片共漏检FN=2,所以 P r e c i s i o n = T P T P + F P = 5 5 + 2 = 0.71 Precision=\frac{TP}{TP+FP}=\frac5{5+2}=0.71 Precision=TP+FPTP=5+25=0.71 在正式介绍ROC之前,我们还要再介绍两个指标,这两个指标的选择使得ROC可以无视样本的不平衡。这两个指标分别是: 假负率(False Negative Rate , FNR) : 真负率(True Negative Rate , TNR),又称特异度 (SPC, specificity): 放在具体领域来理解上述两个指标。如在医学诊断中,判断有病的样本。那么尽量把有病的揪出来是主要任务,也就是第一个指标TPR,要越高越好。而把没病的样本误诊为有病的,也就是第二个指标FPR,要越低越好。不难发现,这两个指标之间是相互制约的。如果某个医生对于有病的症状比较敏感,稍微的小症状都判断为有病,那么他的第一个指标应该会很高,但是第二个指标也就相应地变高。最极端的情况下,他把所有的样本都看做有病,那么第一个指标达到1,第二个指标也为1。 假设总样本中,90%是正样本,10%是负样本。在这种情况下我们如果使用准确率进行评价是不科学的,但是用TPR和FPR却是可以的, AUC对所有可能的分类阈值的效果进行综合衡量。首先AUC值是一个概率值,可以理解为随机挑选 AUC的一般判断标准: 回归任务的评价指标关注预测值和真实值之间的差。 均方误差英文全称为 Mean Squared Error,也称之为 L 2 L2 L2 范数损失。通过计算真实值与预测值的差值的平方和的均值来衡量距离。 平均绝对误差的英文全称为 Mean Absolute Error,也称之为 L 1 L1 L1 范数损失。是通过计算预测值和真实值之间的距离的绝对值的均值,来衡量预测值与真实值之间的距离。 均方根误差的英文全称为 Root Mean Squared Error,代表的是预测值与真实值差值的样本标准差。 参考: https://www.cnblogs.com/guoyaohua/p/classification-metrics.html https://www.cnblogs.com/zhaokui/p/ml-metric.html预测矩形框 ,根据分类器类别分类概率做排序,从小到大分别属于车辆的概率分别为A
最大概率矩形框F开始 ,分别判断A、B、C、D、E与F的重叠度IOU是否大于某个设定的阈值;(3)TP、FP、FN、TN与混淆矩阵
预测为正样本预测为负样本预测正确预测错误
概念
解释
备注
True positives(TP)
预测为 1,预测 正确,即 实际 1
IoU>IOU,IOU一般取0.5
False positives(FP)
预测为 1,预测 错误,即 实际 0
误检
False negatives(FN)
预测为 0,预测 错误,即 实际 1
漏检
True negatives(TN)
预测为 0,预测 正确,即 实际 0
一般不会使用
2.2 准确率(Accuracy)
分类正确的比例,它的计算公式简单直接,表示方法如下:
A c c u r a c y = T P + T N T P + T N + F P + F N Accuracy = \frac{TP + TN}{TP + TN + FP + FN} Accuracy=TP+TN+FP+FNTP+TN
表示如下:
虽然准确率可以判断总的正确率,但是在样本不平衡的情况下,并不能作为很好的指标来衡量结果,举个简单例子,比如正样本占90%,负样本占10%,如果我们全部预测为正样本,那么我们的准确率也能高达90%,但是这样的准确率是没有意义的。2.3 精确率与召回率(Precision , Recall)
预测为正样本的检测框中预测正确的占比。
P r e c i s i o n = T P T P + F P Precision = \frac{TP}{TP + FP} Precision=TP+FPTP精准率代表对正样本结果中的预测准确程度,而准确率则代表整体的预测准确程度,既包括正样本,也包括负样本。
![]()
如上图所示,图中GT共有5只猫待检测,但实际上只检测出来了一只,而且这个检测是正确的。那这种情况下的查准率就是:
P r e c i s i o n = 1 1 = 100 % Precision = \frac{1}{1}= 100\% Precision=11=100%
被正确检测出来的真实框占所有真实框(gt)的比例。
R e c a l l = T P T P + F N Recall = \frac{TP}{TP + FN} Recall=TP+FNTP![]()
同样是上边有5个待检测的GT,这次得到了50个预测框,其中5个全部预测正确,这种情况下TP=5,漏检FN=0最终的查全率为:2.4 F1分数
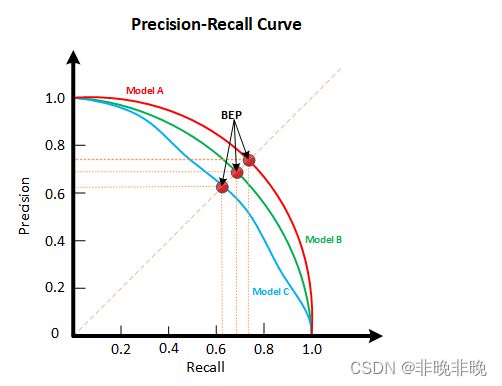
F β = ( 1 + β 2 ) ⋅ p r e c i s i o n ⋅ r e c a l l β 2 ⋅ p r e c i s i o n + r e c a l l = ( 1 + β 2 ) P R β 2 P + R F_β=(1+β^2)⋅\frac{precision⋅recall}{β^2⋅precision+recall}=\frac{(1+β^2)PR}{β^2P+R} Fβ=(1+β2)⋅β2⋅precision+recallprecision⋅recall=β2P+R(1+β2)PR
当β=1称为F1分数,F1是精确率和召回率的调和均值。F1分数同时考虑了查准率和查全率,让二者同时达到最高,取一个平衡。说明:当 β > 1 β>1 β>1时,召回率的权重高于精确率,相反,当 β < 1 β<1 β<1时精确率的权重高于召回率。2.5 G分数
准确率和召回率的几何平均数 。2.6 AP和mAP
AP衡量的是学出来的模型在每个类别上的好坏,mAP(Mean Average Precision)衡量的是学出的模型在所有类别上的好坏,得到AP后mAP的计算就变得很简单了,就是取所有AP的平均值。![]()
在所有的图片中(当前只有上图一张),待检测的目标的数量 n u m o b = 2 num_{ob}=2 numob=2,上图中的检测情况如下表所示:
GT id
Confidence
OB(IoU=0.5)
1
0.98
True
1
0.61
False
对于一个GT来说,只能有一个检测框为正确的检测。![]()
加入第二张图片,此时待检测的目标数量 n u m o b = 3 num_{ob}=3 numob=3,检测情况如下表所示。
GT id
Confidence
OB(IoU=0.5)
1
0.98
True
3
0.89
True
3
0.66
False
1
0.61
False
![]()
GT id
Confidence
OB(IoU=0.5)
1
0.98
True
3
0.89
True
6
0.88
True
7
0.78
True
3
0.66
False
1
0.61
False
4
0.52
True
Rank
Precision
Recall
Confidence thread
1
1.0
0.14
0.98
2
1.0
0.28
0.89
3
1.0
0.42
0.88
4
1.0
0.57
0.78
5
0.80
0.57
0.66
6
0.66
0.57
0.61
7
0.71
0.71
0.52
R e c a l l = T P T P + F N = 5 5 + 2 = 0.71 Recall=\frac{TP}{TP+FN}=\frac5{5+2}=0.71 Recall=TP+FNTP=5+25=0.71
绘制出对应的P-R曲线图:![]()
计算曲线下方的面积,也就是猫这一类别的AP:
( 0.14 − 0 ) × 1.0 + ( 0.28 − 0.14 ) × 1.0 + ( 0.42 − 0.28 ) × 1.0 + ( 0.57 − 0.42 ) × 1.0 + ( 0.71 − 0.57 ) × 0.71 = 0.6694 (0.14−0)×1.0+(0.28−0.14)×1.0+(0.42−0.28)×1.0+(0.57−0.42)×1.0+(0.71−0.57)×0.71=0.6694 (0.14−0)×1.0+(0.28−0.14)×1.0+(0.42−0.28)×1.0+(0.57−0.42)×1.0+(0.71−0.57)×0.71=0.6694对于表格中Recall相同的,只保留Precision最高的值进行计算,最终得到猫这一类的AP=0.6694,如果要计算mAP则需要计算出其他类别的AP,并取平均值。2.7 ROC与AUC
(1)ROC
ROC曲线(receiver operating characteristic curve, 接收者操作特征曲线)有个很好的特性:当测试集中的正负样本的分布变化的时候,ROC曲线能够保持不变。在实际的数据集中经常会出现类别不平衡(Class Imbalance)现象,即负样本比正样本多很多(或者相反),而且测试数据中的正负样本的分布也可能随着时间变化,ROC以及AUC可以很好的消除样本类别不平衡对指标结果产生的影响。ROC和上面做提到的P-R曲线一样,是一种不依赖于阈值(Threshold)的评价指标,在输出为概率分布的分类模型中,如果仅使用准确率、精确率、召回率作为评价指标进行模型对比时,都必须是基于某一个给定阈值的,对于不同的阈值,各模型的指标(Metrics)结果也会有所不同,这样就很难得出一个很置信的结果。真正率(TPR)和假正率(FPR),具体公式如下。
真正率(True Positive Rate , TPR) ,又称:命中率 (hit rate)、敏感度(sensitivity):在所有实际为阳性的样本中,被正确地判断为阳性的比率。
T P R = 正 样 本 预 测 正 确 数 正 样 本 总 数 = T P T P + F N TPR= \frac{正样本预测正确数}{正样本总数}= \frac{TP}{TP+FN} TPR=正样本总数正样本预测正确数=TP+FNTP
其实我们可以发现灵敏度和召回率是一模一样的,只是名字换了而已假正率(False Positive Rate , FPR),又称为错误命中率,假警报率 (false alarm rate) :在所有实际为阴性的样本中,被错误地判断为阳性的比率。
F P R = 负 样 本 预 测 错 误 数 负 样 本 总 数 = F P T N + F P FPR= \frac{负样本预测错误数}{负样本总数}= \frac{FP}{TN+FP} FPR=负样本总数负样本预测错误数=TN+FPFP
F N R = 正 样 本 预 测 错 误 数 正 样 本 总 数 = F N T P + F N FNR= \frac{正样本预测错误数}{正样本总数}= \frac{FN}{TP+FN} FNR=正样本总数正样本预测错误数=TP+FNFN
T N R = 负 样 本 预 测 正 确 数 负 样 本 总 数 = T N T N + F P TNR= \frac{负样本预测正确数}{负样本总数}= \frac{TN}{TN+FP} TNR=负样本总数负样本预测正确数=TN+FPTN因为TPR只关注90%正样本中有多少是被预测正确的,而与那10%负样本毫无关系,同理,FPR只关注10%负样本中有多少是被预测错误的,也与那90%正样本毫无关系。这样就避免了样本不平衡的问题。ROC(Receiver Operating Characteristic)曲线,又称接受者操作特征曲线。该曲线最早应用于雷达信号检测领域,用于区分信号与噪声。后来人们将其用于评价模型的预测能力。ROC曲线中的主要两个指标就是真正率TPR和假正率FPR,上面已经解释了这么选择的好处所在。其中横坐标为假正率(FPR),纵坐标为真正率(TPR),下面就是一个标准的ROC曲线图。(2)AUC
AUC(Area Under Curve)又称为曲线下面积,是处于ROC Curve下方的那部分面积的大小。上文中我们已经提到,对于ROC曲线下方面积越大表明模型性能越好,于是AUC就是由此产生的评价指标。通常,AUC的值介于0.5到1.0之间,较大的AUC代表了较好的Performance。如果模型是完美的,那么它的AUC = 1,证明所有正例排在了负例的前面。一个正样本以及一个负样本 ,分类器判定正样本分值高于负样本分值的概率就是AUC值。简言之,AUC值越大,当前的分类算法越有可能将正样本分值高于负样本分值,即能够更好的分类。
3. 回归任务的评价指标
3.1 MSE
3.2 MAE
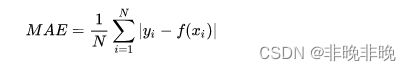
3.3 RMSE

和 MAE 相比,RMSE 对大误差样本有更大的惩罚,但它对离群点敏感,其健壮性不如 MAE。