算法_回溯_递增子序列
文章目录
- 递增子序列
-
- 1.解法
- 2.总结
递增子序列
leetcode链接
1.解法
这道题是一个找子集问题,只不过是要在不改变集合顺序的前提下,从有重复元素出现的集合中,挑选出符合一定条件的子集。(条件指递增并且子集元素数量大于1)
我们先不考虑上面的黑体部分,那么这道题就变为了简单的找子集问题。我们可以先把子集问题的代码写上,不懂子集问题如何求解的可以看我之前的博客(子集)
代码如下:
def subsets(nums):
result = []
path = []
def backtracking(nums,startindex):
path1 = path.copy()
result.append(path1)
for i in range(startindex,len(nums)):
path.append(nums[i])
backtracking(nums,i+1)
path.pop()
backtracking(nums,0)
return result
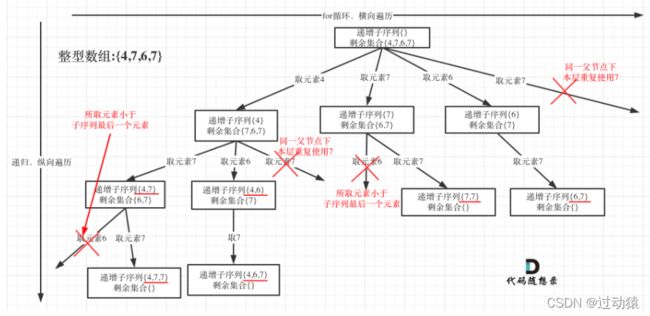
现在我们来考虑以上问题,首先考虑一个比较简单的问题,就是如何判断递增,这个实现起来比较简单。由图可知,只要我们在剩余集合中挑选的元素比已经选到递增子序列中的最后一个元素大(其实是大于等于),举个例子,比如取元素4和7,然后剩余集合就变成了[6,7],那么只要从里面选一个大于等于7的即可。
然后还有一个问题就是子集个数大于1,这点也好实现。可以直接看代码。
所以我们可以对代码做如下修改:
def findSubsequences(nums):
result = [] # 存放最终答案
path = [] # 存放递增子序列
def backtracking(nums,startindex):# startindex是标记剩余集合的在原集合的开始位置
number = float('-inf') # number用来存放path中最后一个值,要初始化为一个最小值
if len(path)>=2: # 当子集元素个数大于2,才能作为答案存入result中
path1 = path.copy()
result.append(path1)
if len(path)>0: # 如果path中有元素,就把number赋值为最后一个值
number = path[-1]
for i in range(startindex,len(nums)):
if nums[i]<number: # 如果取的元素比number小,那么就可以直接跳过;如果大于等于,则需要进一步的递归,找出所有答案
continue
path.append(nums[i])
backtracking(nums,i+1)
path.pop()
backtracking(nums,0)
return result
再考虑有重复元素出现的集合中选择子集,这个问题,我的这个博客中已经讲过(子集II),只要添加以下代码去重即可:
if i>startindex and nums[i]==nums[i-1]:
continue
但是在这道题中行不通,因为上述方法是建立在集合已经排好序的情况下,而这道题的条件就是不能改变集合顺序,因此我们需要另一种方法去重。
为什么要去重?
考虑下面一个例子[1,2,1,1,1,1],如果不进行去重,用上面我们的代码执行出来的结果为:[[1, 2], [1, 1], [1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1, 1], [1, 1], [1, 1, 1], [1, 1, 1, 1], [1, 1], [1, 1, 1], [1,1]]
可以发现后面的 [1, 1], [1, 1, 1], [1, 1, 1, 1]重复了,因为当执行到取第三个1的时候,没有考虑前面已经有了一个1(第一个1),当对这个1进行操作的时候,已经把所有的情况都考虑完了,所以后面在遇到相同的元素的时候(这里是1),就没必要再考虑了,所以我们必须要进行去重
通过上面的分析,我们可以知道如果前面有了一个元素,会把所有的情况都考虑完,到后面出现相同元素时,就没必要考虑了。所以我们可以用一个set来记录哪些元素被使用过了,如果当再次用到该种元素时,就不要考虑了。
修改后的代码如下:
def findSubsequences(nums):
result = []
path = []
def backtracking(nums,startindex):
uset = set() # 定义一个set,记录 **该层下** 哪些元素被使用过了
number = float('-inf')
if len(path)>=2:
path1 = path.copy()
result.append(path1)
if len(path)>0:
number = path[-1]
for i in range(startindex,len(nums)):
if nums[i]<number or nums[i] in uset:# 如果当前元素已经在uset中了,那么就不用考虑了
continue
uset.add(nums[i]) # 每次添加一个元素,uset就要记录一下
path.append(nums[i])
backtracking(nums,i+1)
path.pop()
backtracking(nums,0)
return result
2.总结
不能进行排序的集合,用以下方法去重:
'''
定义一个set,记录 **该层下** 哪些元素被使用过了
注意是定义在递归函数里面,而不要作为全局变量。因为每次递归(每到下一层)都要重新去记录
'''
uset = set()
'''
for循环里面进行判断
'''
if nums[i] in uset:
continue