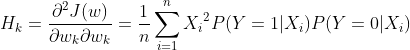逻辑回归(Logistic Regression)
入门小菜鸟,希望像做笔记记录自己学的东西,也希望能帮助到同样入门的人,更希望大佬们帮忙纠错啦~侵权立删。
目录
一、逻辑回归简介与用途
二、逻辑回归的理论推导
1、问题描述和转化
2、初步思路:找一个线性模型来由X预测Y
3、Sigmoid函数(逻辑函数)
4、刚刚的线性模型与Sigmoid函数合体
5、条件概率
6、极大似然估计
7、求最小值时的w的两种方法——补充说明
三、正则化
1、L1正则化
2、L2正则化
四、逻辑回归python实现
1、库函数LogisticRegression中的常用参数的介绍
2、实际应用
五、逻辑回归的优缺点
1、优点
2、缺点
一、逻辑回归简介与用途
逻辑回归是线性分类器(线性模型)—— 主要用于二分类问题
【拓:如何判别一个模型是否为线性模型
理论上分辨:线性模型是可以用曲线来拟合样本的,但是分类的决策边界一定是直线的
数学表达上分辨:表达式中的系数w乘上自变量x(一个w系数影响一个自变量维度x)】
二、逻辑回归的理论推导
前方n多公式预警(如果推错了麻烦跟我说一下,谢谢啦~)
1、问题描述和转化
一个二分类问题给的条件:
分类标签Y {0,1},特征自变量X{x1,x2,……,xn}
如何根据我们现在手头上有的特征X来判别它应该是属于哪个类别(0还是1)
问题的求解转化为:
我们如何找一个模型,即一个关于X的函数来得出分类结果(0或1)
2、初步思路:找一个线性模型来由X预测Y
![]()
但是很明显,这样的函数图像是类似一条斜线,难以达到我们想要的(0或1)的取值
所以我们引入了一个特殊的函数:
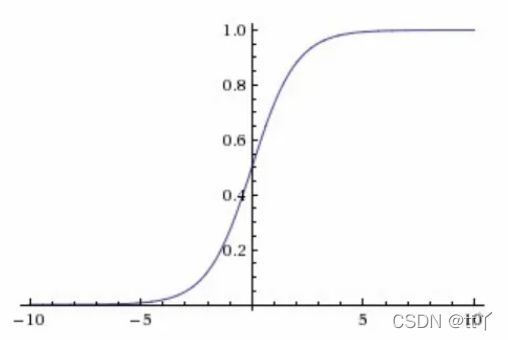
3、Sigmoid函数(逻辑函数)
公式
图像
由图像可见,这样我们就能很好的分类(0或1)
4、刚刚的线性模型与Sigmoid函数合体
第一步:
![]()
第二步:
这样我们就把取值控制在了0或1上,初步达成了我们的目标。
5、条件概率
意义:在特征X的条件下,被划分为Y类别的概率
所以有:
6、极大似然估计
思想:如果一个事件发生了,那么发生这个事件的概率就是最大的。对于样本i,其类别为![]() 。对于样本i,可以把h(Xi)看成是一种概率。yi对应是1时,概率是h(Xi)(即Xi属于1的概率,即上面的p(Y=1|X));yi对应是0时,概率是1-h(Xi)(Xi属于0的概率,即上面的p(Y=0|X))。
。对于样本i,可以把h(Xi)看成是一种概率。yi对应是1时,概率是h(Xi)(即Xi属于1的概率,即上面的p(Y=1|X));yi对应是0时,概率是1-h(Xi)(Xi属于0的概率,即上面的p(Y=0|X))。
即有:
其中i是从0到k(k:属于类别1的个数),i从k+1到n(属于类别0的个数为n-k)。由于y是标签0或1,所以上面的式子也可以写成:
对它取对数,并且除以样本总数n(减少梯度爆炸出现的概率),再乘以负1(将求最大值问题转化为求最小值问题,即转化为求下式的最小值):
化简得:
接下来的任务就是求解当上式最小时的w啦~
7、求最小值时的w的两种方法——补充说明
方法一:梯度下降法(一阶收敛)
通过 J(w) 对 w 的一阶导数来找下降方向,并以迭代的方式来更新参数
(这里的k代表的是第k次迭代;![]() 是我们设定的学习率;
是我们设定的学习率;![]() 就是我们上面所说的
就是我们上面所说的![]() )
)
停止迭代的条件可以是:
(1)到达最大迭代次数
(2)到达规定的误差精度,即
小于等于我们设定的阈值
方法二:牛顿法(二阶收敛)
思想:在现有极小值点的估计值的附近对 f(x) 做二阶泰勒展开,进而找到极小值点的下一个估计值。
假设 ![]() 为当前的极小值点的估计值,则该点的J(w)二阶泰勒展开为:
为当前的极小值点的估计值,则该点的J(w)二阶泰勒展开为:
(注意:这里不是绝对等于,而是近似等于)
当 Δw 无线趋近于0时上式绝对相等,此时上式等价于(相当于上式可以对![]() 求导):
求导):
(但是这里我有点不太明白:为什么上式中的![]() 可以当 Δw 无线趋近于0时近似抵消掉,为什么后面的
可以当 Δw 无线趋近于0时近似抵消掉,为什么后面的![]() 就可以留下来,而不是当成0处理掉,脑袋瓜乱乱的,希望有朋友能跟我说一下,谢谢~)
就可以留下来,而不是当成0处理掉,脑袋瓜乱乱的,希望有朋友能跟我说一下,谢谢~)
因此又可以写为:
其中![]() 为海森矩阵,即:
为海森矩阵,即:
拓展:梯度下降法Vs牛顿法
牛顿法因为是二阶收敛,所以收敛速度很快,但是逆计算很复杂,代价比较大,计算量恐怖
梯度下降法:越接近最优值时,步长应该不断减小,否则会在最优值附近来回震荡,计算相对来说会简单一些。
三、正则化
正则化的意义:避免过拟合。
模型如果很复杂,变量值稍微变动一下,就会引起预测精度的问题。正则化可以避免过拟合的原因就是它降低了特征的权重,使得模型更简单。
主要思想:保留所有的特征变量,因为我们不太清楚要舍掉哪个特征变量,并且又想尽可能保留信息。所以我们只能是惩罚所有变量,让每个特征变量对结果的影响值变小,这样的话你拟合出来的模型才会更光滑更简单,从而减少过拟合的可能性。
1、L1正则化
![]()
即损失函数再加一项正则化系数![]() 乘上L1正则化表达式
乘上L1正则化表达式
(![]() 决定惩罚力度,过高可能会欠拟合,过小无法解决过拟合)
决定惩罚力度,过高可能会欠拟合,过小无法解决过拟合)
作用:L1正则化有特征筛选的作用,对所有参数的惩罚力度都一样,可以让一部分权重变为零(降维),因此产生稀疏模型,能够去除某些特征(权重为0则等效于去除)
2、L2正则化
![]()
即损失函数再加一项正则化系数![]() 乘上L2正则化表达式
乘上L2正则化表达式
作用:使各个维度权重普遍变小,减少了权重的固定比例,使权重平滑
四、逻辑回归python实现
1、库函数LogisticRegression中的常用参数的介绍
from sklearn.linear_model import LogisticRegression(1)penalty:表示惩罚项(正则化类型)。字符串类型,取值为’l1’ 或者 ‘l2’,默认为’l2’。
l1:向量中各元素绝对值的和,作用是产生少量的特征,而其他特征都是0,常用于特征选择;
l2:向量中各个元素平方之和再开根号,作用是选择较多的特征,使他们都趋近于0。
注意:如果模型的特征非常多,我们想要让一些不重要的特征系数归零,从而让模型系数稀疏化的话,可以使用l1正则化。
(2)tol:浮点型,默认为1e-4;表示迭代终止判断的误差范围
(3)C:浮点型(为正的浮点数),默认为1.0;表示正则化强度的倒数(目标函数约束条件)。数值越小表示正则化越强。
(4)solver:用于优化问题的算法。取值有{'newton-cg', 'lbfgs', 'liblinear', 'sag', 'saga'},默认为'liblinear';
对于小数据集来说,“liblinear”就够了,而“sag”和'saga'对于大型数据集会更快。
对于多类问题,只有'newton-cg', 'sag', 'saga'和'lbfgs'可以处理多项损失;“liblinear”仅限于一对一分类。
注意:上面的penalty参数的选择会影响参数solver的选择。如果是l2正则化,那么4种算法{‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’}都可以选择。但如果penalty是l1正则化的话,就只能选择‘liblinear’了。这是因为L1正则化的损失函数不是连续可导的,而{‘newton-cg’, ‘lbfgs’,‘sag’}这三种优化算法时都需要损失函数的一阶或者二阶连续导数。而‘liblinear’并没有这个依赖。
(5)multi_class:字符串类型,取值有{ovr', 'multinomial'},默认为'ovr';
如果选择的选项是“ovr”,那么则为“one-versus-rest(OvR)”分类。multinomial则为“many-vs-many(MvM)”分类。
“one-versus-rest(OvR)”分类:无论你是多少元的逻辑回归,都可以看做多个二元逻辑回归的组合。具体做法是:对于第K类的分类决策,我们把所有第K类的样本作为正例,除了第K类样本以外的所有样本都作为负例,然后在上面做二元逻辑回归,得到第K类的分类模型。其他类的分类模型获得以此类推。
“many-vs-many(MvM)”分类:如果模型有T类,我们每次在所有的T类样本里面选择两类样本出来,不妨记为T1类和T2类,把所有的输出为T1和T2的样本放在一起,把T1作为正例,T2作为负例,进行二元逻辑回归,得到模型参数。我们一共需要T(T-1)/2次分类(即组合数
)。
(6)n_jobs:整数类型,默认是1;
如果multi_class='ovr' ,则为在类上并行时使用的CPU核数。无论是否指定了multi_class,当将
' solver ’设置为'liblinear'时,将忽略此参数。如果给定值为-1,则使用所有核。
2、实际应用
来个简单的小栗子
我们使用sklearn里的乳腺癌数据集
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()然后对数据进行一个处理,让我们看起来舒服点,计算机处理也舒服点
data=cancer["data"]
col = cancer['feature_names']
x = pd.DataFrame(data,columns=col)#就是那些个特征
target = cancer.target.astype(int)
y = pd.DataFrame(target,columns=['target'])#对应特征组合下的类别标签训练集测试集分分类
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.3,random_state=1)直接进入训练
model = LogisticRegression()#默认参数
model.fit(x_train, y_train)训练出来的模型对test集进行一个预测
y_pred = model.predict(x_test)
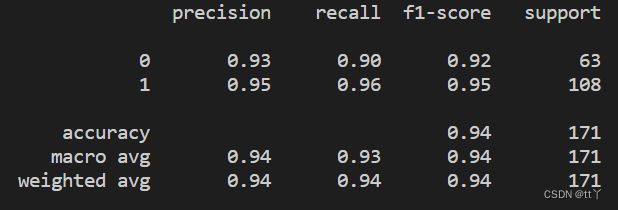
print(classification_report(y_test, y_pred))完整代码如下:
from sklearn.datasets import load_breast_cancer
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report
import warnings
warnings.filterwarnings('ignore')
cancer = load_breast_cancer()
data=cancer["data"]
col = cancer['feature_names']
x = pd.DataFrame(data,columns=col)
target = cancer.target.astype(int)
y = pd.DataFrame(target,columns=['target'])
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.3,random_state=1)
model = LogisticRegression()
model.fit(x_train, y_train)
y_pred = model.predict(x_test)
print(classification_report(y_test, y_pred))我们训练出的模型的效果如下:
五、逻辑回归的优缺点
1、优点
(1)适合分类场景
(2)计算代价不高,容易理解实现。
2、缺点
(1)容易欠拟合,分类精度不高。
(2)数据特征有缺失或者特征空间很大时表现效果并不好。
欢迎大家在评论区批评指正,谢谢啦~
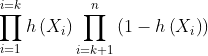
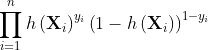

![J(w)=min(-\frac{1}{n} \sum_{i=1}^{n}\left[y_{i}\left(w^{T} x+b\right)-\ln \left(e^{w^{T} x+b}+1\right)\right])](http://img.e-com-net.com/image/info8/0704376d045a4c89ad820f9e503952d2.gif)