基于剑指Offer整理总结Python知识点
持续更新
为了熟练python和算法,此次使用Python3刷题。由于过往Python多半直接使用,基础了解极少,刷题同时会记录一些Python有关的知识点。
目录
- Python
-
- 基础内容
-
- 小知识
- 浅拷贝和深拷贝
- String
- List
- Dict与Hash
-
- Dict
- 哈希表
- Numpy
- Queue和deque
- Counter
- 正则
- 位运算
- 算法与数据结构
-
- 链表
-
- LRU和LFU
- 排序
-
- 冒泡排序
- 选择排序
- 插入排序
- 希尔排序(shell sort)
- 归并排序
- 快速排序
- 堆排序
- 计数排序
- 桶排序
- 基数排序
- 二叉树
-
- 二叉搜索树
- 队列
-
- 优先队列(Priority Queue)
- 剑指Offer
-
- Stack&Queue
-
- 剑指09
- 剑指30
- 链表
-
- 剑指06
- 剑指24
- 剑指35
- String
-
- 剑指 05
- 剑指58
Python
基础内容
小知识
倒叙for循环
# 前开后闭,-1为步长,输出10至0
for i in range(10,-1,-1):
self:
Python规定在类下,函数的第一个参数是实例对象本身。1
__init__():
两个下划线开头的函数是私有函数,外部无法使用或访问。init函数主要用于初始化类中变量。
函数中的->:
用于标记该函数返回值的类型。def test(name) -> str表示该函数返回类型为str
type hint:
跟在函数参数冒号后的解释def test(name:str)表示name是str类型。
除此之外还有Union和Optional:
def test(name:Union[str,int]),表示name可以是str也可以是int
def test(name:Optional[str]),表示name可以是str也可以是None
切片:
a[start:stop] # 元素从start开始到stop-1
a[start:] # 元素从start开始到结束
a[:stop] # 元素从头开始到stop-1结束
a[:] # copy整个列表
a[start:stop:step] # 元素从start开始算每step个输出,并不超过stop-1(可包含)
a[-1] # 列表中最后一个元素
a[-2:] # 列表中最后两个元素
a[:-2] # 列表中所有元素除了最后两个
a[::-1] # 列表中元素全部倒序
a[1::-1] # 最开始两个元素倒序
a[:-3:-1] # 最后两个元素倒序
a[-3::-1] # 除了最后两个元素都倒序
当选取的切片超过列表长度,只会返回 [ ],不会报错。
浅拷贝和深拷贝
TODO:
String
strip():删除string头尾所有的空白字符。其他内容
replace(old,new):替换string中所有old变成new,且原string是不会更改的!只有s.replace(old,new)输出是更改的。
List
顺序表:2
顺序表即按照顺序将数据地址连续的存储在内存的一处地方。有两种结构的顺序表:一体式结构和分离式结构。
为了在内存中开辟一块区域来连续存放就需要告诉它要多少地,如果后续数据溢出还需要重新申请空间。
一体式结构顺序表:将头信息(容量、目前元素个数)和元素数据放在一起。
优点:整体性强,易于管理。
缺点:扩充时,头信息和元素需要一起切换到新区域。需要更改顺序表对象。

分离式结构顺序表:将头信息和元素分开存放,并将元素地址给头信息从而建立链接。
优点:扩充时,只要修改头信息后的链表地址,使得顺序表对象地址无需改变。

List数据结构:
Python的list结构是一种分离式技术的动态顺序表,是Stack。
List扩充:
1.线性增长:每次扩充固定数量的存储位置。优点:节省空间。缺点:遇到扩充大空间时,操作次数多。(时间换空间)
2. 指数增长:每次扩充的容量加倍。优点:操作次数少,但浪费空间资源。(空间换时间)
List寻址:
由于list可以存储不同类型数据,所有有两种寻址方法。
1.存储相同类时:相同类型所占字节一致,可以根据逻辑和物理地址计算偏移量寻址,时间复杂度O(1)
2. 存储不同类型:由于字节数不同,所以此时存储元素地址,元素外置。时间复杂度O(1)。
其他:
内置函数len()的时间复杂度也是O(1),因为底层会维护一个size变量,在append时候就做记录。
Dict与Hash
Dict
由Key和value配对组成的集合,可变容器,可存储任意类型对象。3
字典有序
Python3.5(含)之前,字典无序,即无法保证你插入键值的顺序与输出的顺序一致。例:输入键值对A键值对B,输出可能为键值对B键值对A。
Python3.6开始,字典有序,并且效率更高。
字典原理:
1.Python < 3.6
CPython底层初始化8行3列数组,每一列内容为“hash值,指向键的指针,指向值的指针”。
其中Hash值为当前运行时的值,即每一次python运行,同一个键的hash值可能是不一样的。(如果需要可重现可跨进程的hash值则需要用到hashlib,详见下方hashlib。)
由于有8行,所以需要hash值对8取余,将结果放入对应的行数。(字典插入快满了或者重复余数怎么办:开放寻址、扩容,后面哈希表详细说明)
my_dict['name'] = "kingname"
my_dict['age'] = 26
my_dict['salary'] = 999999
'''
此时的内存示意图
[[-4234469173262486640, 指向salary的指针, 指向999999的指针],
[1545085610920597121, 执行age的指针, 指向26的指针],
[---, ---, ---],
[---, ---, ---],
[---, ---, ---],
[1278649844881305901, 指向name的指针, 指向kingname的指针],
[---, ---, ---],
[---, ---, ---]]
'''
当输出字典的时候,遍历此数组并显示,所以输出顺序是数组里存放的顺序,而且会存在有些行并没有内容。
2.Python >=3.6
底层初始化一个长度为8的一维数组和一个空的二维数组。
my_dict['name'] = 'kingname'
'''
此时的内存示意图
indices = [None, 0, None, None, None, None, None, None]
entries = [[-5954193068542476671, 指向name的指针, 执行kingname的指针]]
'''
indices中存储位置的选择是依据hash%8,内容由原来的键值变成了二维数组的索引(也可以理解为存入的次序),而二维数组存储的内容则为hash值、键值对。
寻找的过程:例如hash%8 = 2,则去找indices[2],再根据indices[2]的结果去找对应entries中的内容,即entries[indices[2]]。
当输出时,我们只要遍历entries就可以看到我们输入时的顺序,也不存在空行跳过的情况。
对比:< 3.6,一个元素占8bytes,就算只有三行有效数据,二维数组占总内存8*8*3 = 192 bytes;>=3.6,entries有多少内容占多少,有三行则只占3*8*3 = 72 bytes,一位数组indices只占8bytes。内存占用只有原来41%。
hashlib模块:
hashlib会提供常见的摘要算法,例如MD5,SHA1等,将信息通过某种算法转换成摘要。此时生成的信息摘要将不会想hash()那样每次运行时会有所不同。
相关函数:
1.get(), set(), contains():根据上述原理(计算并寻找index),平均都为O(1),但如果情况糟糕(详见下方hash之开放寻址),则为O(n)。
2.dict.setdefault(key, value):当dict中没有key时,给予默认值value,如果有则不变。
3.defaultdict:当字典里的key不存在却又被查找时,不返回keyError而返回默认值。setdefault是dict底下的函数,defaultdict是collections下的,并且不能够设置详细固定值。
from collections import deafultdict
# factory_function 可以是int、str、list等,也可以是函数,例如lamda:0
# dict = defaultdict(factory_function)
dict1 = defaultdict(int) # 0
dict2 = defaultdict(set) # set()
dict3 = defaultdict(str) #
dict4 = defaultdict(list) # []
dict5 = {}
dict5.get('k',0) # 如果key不存在则得到 0
- 找dict中value最大的key的方法可以用 max_key = max(dicts, key=dicts.get)
哈希表
线性表存储结构,由一个直接寻址表和哈希函数组成(hash(key))。
字典是哈希表的应用之一,简单的插入方法和上方字典描述的一致。
解决哈希冲突:
①开放寻址(Python中用的):
a. 线性探查:i被占用就找i+1,不行就i+2
b. 二次探查:i+12,i-12,i+22,i-22…
c. 二度哈希:n个哈希函数,用h1发生冲突则使用h2,h3…
②拉链法:
哈希表每个位置后方链接链表,当冲突时向后增加。

③再散列:
对冲突值再放进hash函数。
HashTable与Dict的区别:4
①多线程使用哈希表,因为哈希表线程安全。
②字典是泛型,数据无需拆装箱,效率高,哈希表与之相反。
③python>=3.6后dict中元素的排列顺序是有序,但是哈希表不是。
TODO:为什么是线程安全,Concurrenthashmap
手撕hashtable:
https://blog.csdn.net/weixin_36313588/article/details/114455914
https://www.cnblogs.com/pungchur/p/12079853.html
https://www.zhijinyu.com/article/143/detail/
Numpy
Numpy中支持二维数组的slice,主要通过以下形式:
A = np.array([
[0.3777, 0.0110, 0.0009, 0.0084],
[0.0008, 0.0002, 0.7968, 0.0005],
[0.0068, 0.0102, 0.1011, 0.1012],
[0.1147, 0.0021, 0.0002, 0.2157]
])
y = A[0:2,0:2] # 选取A中0行0列开始,1行1列结束
# 输出 [0.3777,0.0110
# 0.0008,0.0002]
y = A[:, 0] # 提取了所有行的第一列
TODO:
等比
#不写base默认以10为底,从10x开始到10y结束,共z个
a = np.logspace(x,y,z,base=2)
Queue和deque
https://zhuanlan.zhihu.com/p/146393319
Counter
https://blog.csdn.net/sinat_28576553/article/details/99131954
正则
python正则文档
r’xx’:规则中前面会有r的时候意味着后面是原生字符串(raw string),这样就不需要额外的转义字符,但如果没有,在特殊字符前需要4个反斜杠,正则需要转化一次,python解释器需要转化一次。
re.escape(String):
String里如果遇到在正则规则中会表示特殊字符的字符时,前面会添加 “\”。
例子:包含英文字母、数字、下划线、中划线,并且长度在6-16位,规则为'^[a-zA-Z0-9_-]{6,16}$'
在里面可以看到有字符"[","^"等,这些在正则表达式里面都有特殊的含义,所以当要去自定义一个正则表达式时就要避免里面出现这类特殊含义的字符,为了解决只好在特殊字符前面添加“\”以实现转义。re.escape就可以自动实现,将re.escape(reg)输出'\^\[a\-zA\-Z0\-9\_\-\]\{6\,16\}\$'
re.compile(reg):
将正则表达式的样式编译为一个 正则表达式对象 (正则对象),可以直接用于匹配或者查找,这样可以省去每次都写一长串自定义的规则,再去调用相关函数。
例子:
pw_rule = re.compile(r'^[a-zA-Z0-9_-]{6,16}$')
result = pw_rule.match("!@#$%^&*(Ivan2345678Ivan2345678")
# result 返回None, 因为无法找到和正则表达式相匹配的string
# 上面code相当于
result = re.match(r'^[a-zA-Z0-9_-]{6,16}$',"!@#$%^&*(Ivan2345678Ivan2345678")
re.sub(pattern, new, origin)
根据pattern去匹配,如果匹配上就把origin里面匹配上的部分都换成new。
例子:
re.sub(r'[0-9]', '*', "今天是2022年3月")
# 今天是****年*月
sub的详细介绍
re.split(pattern, string):
根据pattern的内容去分割String。
例子:
匹配不是单词的内容,根据他们去对string进行分割。
re.split(r'\W+','w1,,w2,w3.')
# ['w1','w2','w3','']
re.split(r'\W','w1,,w2,w3.')
# ['w1','','w2','w3','']
re.findall(pattern, string) 和 re.finditer(pattern, string)
findall找出所有的匹配项并且存在list里,如果一个匹配里面要拆分几个小匹配,就会有tuple框起来。
content = '''
email:[email protected] email:[email protected] email:[email protected]
'''
print(re.findall(r"((\d+)@(\w+).com)", content))
# [('[email protected]', '12345678', '163'), ('[email protected]', '2345678', '163'), ('[email protected]', '345678', '163')]
finditer会输出一个迭代对象,这个对象会包括所有的匹配项,就相当于把findall里面每一个tuple变成了一个对象。
s = re.finditer(r"((\d+)@(\w+).com)", content)
for s1 in s:
print(s1)
'''
span里面是匹配的start和end位置,可以通过s1.start()和s1.end()分别获取
'''
如果要获得每个匹配值可以使用group()函数,就相当于在findall里面通过index获取对应元素:
for s1 in s:
print("对象 ", s1)
print("group 0 ", s1.group()) # 相当于group(0) 会输出最完整的匹配对象
print("group 1 ", s1.group(1)) # 输出第一个匹配大括号的东西
print("group 2 ", s1.group(2)) #输出最左小括号匹配的
print("group 3 ", s1.group(3)) # 输出右边小括号匹配的东西
'''
对象
group 0 [email protected]
group 1 [email protected]
group 2 12345678
group 3 163
对象
group 0 [email protected]
group 1 [email protected]
group 2 2345678
group 3 163
对象
group 0 [email protected]
group 1 [email protected]
group 2 345678
group 3 163
'''
位运算
TODO:
Python 负数的存储:
Python,Java 等语言中的数字都是以 补码 形式存储的。但 Python 没有 int , long 等不同长度变量,即在编程时无变量位数的概念。
获取负数的补码: 需要将数字与十六进制数 0xffffffff 相与。可理解为舍去此数字 32 位以上的数字(将 32 位以上都变为 00 ),从无限长度变为一个 32 位整数。
返回前数字还原: 若补码 aa 为负数( 0x7fffffff 是最大的正数的补码 ),需执行 ~(a ^ x) 操作,将补码还原至 Python 的存储格式。 a ^ x 运算将 1 至 32 位按位取反; ~ 运算是将整个数字取反;因此,` ~(a ^ x) 是将 32 位以上的位取反,1 至 32 位不变。
(或者参考链接,但属实没必要话贼多时间在这上面。)
算法与数据结构
TODO:常见的字符串匹配;
位运算,二叉树,链表,dc,dp,递归,图(dfs等),排序,滑动窗口
链表
LRU和LFU
LRU (Least recently used) 最近最少使用,以最近一次访问时间为参考。
LFU (Least frequently used) 最近一次被访问次数最少的数据,以次数为参考。
LFU
基本思路(参考 leetcode 432):
-
一个根据出现次数从小递增的双向链表。为维护双向链表,需要先建一个Node对象,对象包含一个指向前Node的指针,一个指向后Node的指针,包含出现相同数量的string(内容)和具体数量。
图表示"hello"和"bye"都出现了1次。

-
一个hashmap(dict),维护当前出现的键及其对应值,键为string(内容),值为string所在的node对象。以上图为例,目前dict应该为下图形式:

-
插入操作。简单从两个角度思考,在链表中新建节点还是加入现有节点。
这里以insert("hello"), insert("bye"), insert("hello")三个操作为例:
a. 最开始初始链表头节点root,因为什么都没有,所以这里是新建节点

b. 新加入了"bye",正好之前的“hello”次数也是1,就加入这个节点。

c. 这一步又加了“hello”,出现了没出现的次数,所以新建节点,同时需要当前Node中keys的"hello"删掉。

-
删除操作:和插入类似,也是加入现有node 或 新建node。但除此之外,当要删除的string数量只有1的时候,我们也需要将它从dict中删掉,然后从node里移除。
如果删除后,keys为空了,那么会留下空的node,也需要将其链表中删掉。
代码:.
class Node:
def __init__(self, key="", count=0):
self.keys = {key}
self.count = count
self.prev = None
self.next = None
# 双链表,在当前节点后增加
def insert(self, node: 'Node') -> 'Node':
node.prev = self
node.next = self.next
self.next.prev = node
self.next = node
return node
# 双链表,删除当前节点
def remove(self):
self.prev.next = self.next
self.next.prev = self.prev
class AllOne:
def __init__(self):
# 初始空表头
self.root = Node()
self.root.prev = self.root
self.root.next = self.root
self.dict = {}
def inc(self, key: str) -> None:
# 当前key没有出现过,需要向dict增加
if key not in self.dict:
# 由于是第一次出现,所以一定会插在表头后面
# 这个时候要判断是新建节点,还是加入已有节点
# 当链表还是空的,或者当前最小的节点出现的次数不是1,那么就要新建节点
if self.root.next is self.root or self.root.next.count != 1:
self.dict[key] = self.root.insert(Node(key,1))
else:
# 直接添加到已有节点
self.root.next.keys.add(key)
self.dict[key] = self.root.next
else:
# 当前key出现过,去找其现在所在节点
cur = self.dict[key]
# 并看看他下一个节点的count和自己差多少
nxt = cur.next
# 如果当前所在位置是最大值,或者下一个节点的count和自己的不连续,那么就要新建节点
if nxt is self.root or nxt.count != cur.count + 1:
# 在当前节点后面加入
self.dict[key] = cur.insert(Node(key,cur.count+1))
else:
# 直接添加到已有节点,就是nxt
nxt.keys.add(key)
# 更新dict中的node
self.dict[key] = nxt
# 移除当前节点中的key
cur.keys.remove(key)
# 如果移除这个之后,node的keys就没东西了,那就可以把这个node从链表中删除
if(len(cur.keys))==0:
cur.remove()
def dec(self, key: str) -> None:
cur = self.dict[key]
# 如果当前key只有一个,那就直接在dict中删除了
if cur.count == 1:
del self.dict[key]
else:
pre = cur.prev
# 如果当前节点的前一个count和cur的count不连续或者前面一个节点就是root,就要创建新的节点
if pre is self.root or cur.count - 1 != pre.count:
self.dict[key] = cur.prev.insert(Node(key,cur.count-1))
# 如果连续,则直接加入当前节点
else:
pre.keys.add(key)
self.dict[key] = pre
cur.keys.remove(key)
# 如果移除这个之后,node的keys就没东西了,那就可以把这个node从链表中删除
if(len(cur.keys))==0:
cur.remove()
def getMaxKey(self) -> str:
# root的前一个就是最大的,next帮助返回第二个iter中的东西
return next(iter(self.root.prev.keys)) if self.root.prev is not self.root else ""
def getMinKey(self) -> str:
# root后一个就是最小的
return next(iter(self.root.next.keys)) if self.root.next is not self.root else ""
# Your AllOne object will be instantiated and called as such:
# obj = AllOne()
# obj.inc(key)
# obj.dec(key)
# param_3 = obj.getMaxKey()
# param_4 = obj.getMinKey()
LRU
TODO: 参考leetcode 146
排序
参考链接
冒泡排序
def bubblesort(arr):
if len(arr) < 2:
return arr
for outer in range(1, len(arr)):
# 不看最后outer个,第一次循环不看最后一个,第二次不看最后两个
for inner in range(0, len(arr) - outer):
# 如果前者大于后者就交换位置
if arr[inner] > arr[inner + 1]:
temp = arr[inner]
arr[inner] = arr[inner + 1]
arr[inner + 1] = temp
return arr
- 特性
a. 平均时间复杂度: O ( n 2 ) O(n^2) O(n2),两次for循环
b. 最好情况: O ( n ) O(n) O(n)。在swap的模块设置一个flag,如果flag显示没有交换,那就说明当前arr已经排序。只需要遍历一次arr即可。
c. 最坏情况: O ( n 2 ) O(n^2) O(n2),全部倒序的时候
d. 空间复杂度: O ( 1 ) O(1) O(1)
e. 排序方式:In-Place(占用常数内存,不占用额外内存)
f. 稳定:排序前后相等键值的顺序不变。
选择排序
def selectsort(arr):
if len(arr) < 2:
return arr
# 循环n遍,每循环一次少循环一次
for i in range(len(arr) - 1):
# 记录最小值位置
min = i
for j in range(i, len(arr) - 1):
if arr[min] > arr[j + 1]:
min = j + 1
print(arr[min])
# 交换最小和最前面的位置
temp = arr[min]
arr[min] = arr[i]
arr[i] = temp
return arr
- 特性
a. 平均时间复杂度: O ( n 2 ) O(n^2) O(n2),不管怎么样,他都要遍历 n 2 n^2 n2遍。
b. 最好情况: O ( n 2 ) O(n^2) O(n2)
c. 最坏情况: O ( n 2 ) O(n^2) O(n2)
d. 空间复杂度: O ( 1 ) O(1) O(1)
e. 排序方式: In-Place
f. 不稳定
插入排序
- 步骤:
从数组第二个元素开始遍历,比较前面所有的元素,并把当前元素放在顺序位置上。类似打扑克,手上抓了一副乱七八糟的牌,然后你就从最左边开始,挨个排序,保证左侧的牌都是有序的。 - 图例
从第二个开始看,前面的比自己大的话就往前换,换,换到头或者换到比自己小的元素的时候就停止;然后开始第二次循环…

- 代码
def insertsort(arr):
if len(arr) < 2:
return arr
# 外圈循环,要遍历每一个数字这样才能去插入
for i in range(1, len(arr)):
j = i
# 里圈循环,从当前元素向前循环对比大小并置换
while j > 0:
if arr[j] < arr[j-1]:
temp = arr[j]
arr[j] = arr[j-1]
arr[j-1] = temp
else:
break
j -= 1
return arr
- 特性
a. 平均时间复杂度: O ( n 2 ) O(n^2) O(n2)
b. 最好情况: O ( n ) O(n) O(n),所有的都是排序好的,这样里圈循环就直接break。
c. 最坏情况: O ( n 2 ) O(n^2) O(n2)
d. 空间复杂度: O ( 1 ) O(1) O(1)
e. 排序方式:In-Place
f. 稳定
希尔排序(shell sort)
- 插排的改进,由于插排只有在已排序的数组中有线性时间复杂度,在未排序数组中需要一个一个换位。所以希尔排序是先将待排数组分成若干子序列(即只看间隔n的那些数字),先进行插排,然后再整体插排。
- 步骤:
一般选取间隔的方法是:第一次循环选择间隔 N / 2 N/2 N/2的元素进行排序,第二次循环选择间隔 N / 4 N/4 N/4的元素进行排序,如此往复,间隔为1的时候就是插排,然后间隔为0的时候排序完成。(其他排序可见链接,希尔排序的性能取决于是如何选取间隔的。) - 图例:
以sequence: N / 2 , N / 4 , . . . , 1 N/2, N/4, ... , 1 N/2,N/4,...,1为例子,其中 N N N为元素个数。此处 N = 5 N=5 N=5, N / 2 = 2 N/2=2 N/2=2意味着排序第0位、第2位、第4位…的数字。然后

- 代码
def shellsort(arr):
if len(arr) < 2:
return arr
seq = 2
while math.floor(len(arr) / seq) != 0:
gap = math.floor(len(arr) / seq)
print("gap ", gap)
# 从第二个元素开始
i = 1
# 跟踪看间隔的下标会不会out of range
while i * gap < len(arr):
# 当前元素坐标
j = i * gap
# 插排,循环往前看间隔的gap位置元素,放在正确位置上
while j > 0:
if arr[j] < arr[j - gap]:
temp = arr[j]
arr[j] = arr[j - gap]
arr[j - gap] = temp
j -= gap
i += 1
print("arr ", arr)
seq *= 2
return arr
"""
input = [47, 4, 5, 24, 63, 16, 8, 45, 6, 33, 9]
output:
gap 5
arr [9, 4, 5, 24, 63, 16, 8, 45, 6, 33, 47]
gap 2
arr [5, 4, 6, 24, 8, 16, 9, 45, 47, 33, 63]
gap 1
arr [4, 5, 6, 8, 9, 16, 24, 33, 45, 47, 63]
[4, 5, 6, 8, 9, 16, 24, 33, 45, 47, 63]
"""
- 特性
a. 平均时间复杂度: O ( n l o g n ) O(nlogn) O(nlogn)
b. 最好情况: O ( n l o g 2 n ) O(nlog^2n) O(nlog2n)
c. 最坏情况: O ( n l o g 2 n ) O(nlog^2n) O(nlog2n)
d. 空间复杂度: O ( 1 ) O(1) O(1)
e. 排序方式:In-Place
f. 不稳定
归并排序
典型的分而治之(Divide and Conquer)算法应用。
-
步骤
代码分成两个部分,一个是对半拆分数组,第二个是通过两个指针合并两个数组。当待合并的两个数组有一个走到头了,那就直接将剩下的数组直接复制到已经合并的数组后面。 -
代码
def merge(left, right):
m = []
l = r = 0
# 左右两个数组依次对比
while l < len(left) and r < len(right):
if left[l] < right[r]:
m.append(left[l])
l += 1
else:
m.append(right[r])
r += 1
if l == len(left):
while r < len(right):
m.append(right[r])
r += 1
else:
while l < len(left):
m.append(left[l])
l += 1
return m
def mergeSort(arr):
# base case
if len(arr) == 1:
return arr
# 将arr分成左边和右边
mid = math.floor(len(arr) / 2)
# 不停拆分
left = mergeSort(arr[:mid])
right = mergeSort(arr[mid:])
# 不停合并
return merge(left, right)
arr = [47, 4, 5, 24, 63, 16, 8, 45, 6, 33, 9]
print(mergeSort(arr))
- 特性
a. 平均时间复杂度: O ( n l o g n ) O(nlogn) O(nlogn)
b. 最好情况: O ( n l o g n ) O(nlogn) O(nlogn)
c. 最坏情况: O ( n l o g n ) O(nlogn) O(nlogn)
d. 空间复杂度: O ( n ) O(n) O(n)
e. 排序方式:Out-Place
f. 稳定
快速排序
同样是分而治之的应用之一,可以说是超级好的排序算法了。
- 步骤
主要步骤是通过选取数组中一个数字pivot,然后通过遍历数组与pivot比较,把小的放在pivot左边,大的放右边。然后接着对两边的数组做同样的事情。
(可以看出如果pivot选的正好是中位数,那排序速度就最快了,TODO:有个关于选pivot的算法在ucsd笔记上) - 图例
pivot的位置在遍历完之后和那个处于分界的数字进行交换。

- 代码
def quicksort(arr, left, right):
if left < right:
# 得到分界索引 pi
pi = partition(arr, left, right)
# 快排左数组
quicksort(arr, left, pi - 1)
# 快排右数组
quicksort(arr, pi + 1, right)
print(arr)
return arr
def partition(arr, left, right):
# 记录待比较的pivot
pivot = arr[left]
# 记录小数值区域的最后一个元素的位置
small = left
# 用range的话会没办法循环到最后一个元素,所以这里+1了
for i in range(left,right+1):
if arr[i] < pivot:
# 如果小,那么小数值区域的最后一个元素位置后移
small += 1
# 交换当前元素i和small位数值
temp = arr[i]
arr[i] = arr[small]
arr[small] = temp
# 遍历到结尾,再交换小数值区域最后一个元素与pivot的位置
arr[left] = arr[small]
arr[small] = pivot
return small
arr = [47, 4, 5, 24, 63, 16, 8, 45, 6, 33, 9]
print(quicksort(arr,0,len(arr)-1))
- 特性
a. 平均时间复杂度: O ( n l o g n ) O(nlogn) O(nlogn)
b. 最好情况: O ( n l o g 2 n ) O(nlog^2n) O(nlog2n)
c. 最坏情况: O ( n 2 ) O(n^2) O(n2)
d. 空间复杂度: O ( n l o g n ) O(nlogn) O(nlogn)
e. 排序方式:In-Place
f. 不稳定
堆排序
分最大堆排序和最小堆排序,最大堆排序即子节点的键值或索引总是小于等于其父节点。
堆可以理解成一个满足一定条件的完全二叉树。
最大堆和最小堆称为二叉堆,它是一棵二叉完全树(即除了可能是最后一层之外,所有的层次都被完全填满了,而且最后一层的所有键都是在左边)。也正是这个属性使得下方我们一颗把它和数组的索引进行对应。
数组index和堆排序对应的关系

总结为当父节点是 i i i时,其左子节点为 2 ∗ i + 1 2*i+1 2∗i+1,右子节点为 2 ∗ i + 2 2*i+2 2∗i+2。
本文通过最大堆排序来获得从小到大排序的数组。
-
步骤
a. 根据数组和堆的索引对应关系,我们可以先遍历所有可能的父节点,如果数组长度为 n n n,那么第 n / / 2 n // 2 n//2个元素就是最后一个父节点,其索引为 n / / 2 − 1 n // 2 - 1 n//2−1。比如,现在有四个节点,那最后一个父节点将会是位于数组第二个位置(index=1)的元素。
b. 然后通过递归判断每个父节点的左右子节点是否比自己大
如果大则交换位置并记录当前最大元素所在处
如果小则不交换
如果当前位置*(父节点)就是最大元素所在位置,递归结束。完成最大堆创建。
c. 最大堆的终极父节点一定是数组中最大的数字,所以把它拿出来,然后和老末交换位置,这样就可以确定当前最大的元素。
d. 老末放到根节点去之后会打破最大堆,所以继续堆化找到下一个最大值。 -
图例
此处演示了从最后一个父节点开始,判断它和它子节点的大小。当最底下两层完成大小交换之后,到了倒数第三层的父节点。
当在第三层父节点比其子节点小之后,它会进行交换,交换完成之后还需要判断交换位置的元素的子节点们(也就是最后一层)是否会比该元素大(这里就需要通过递归实现)。
-
代码
# 堆化
def heapify(arr, n, i):
# 先记录父节点索引是最大值索引
largest = i
# 算出它左右子树索引
l = 2 * i + 1
r = 2 * i + 2
# 先看左子树是不是存在,并且是不是比父节点大
if l < n and arr[i] < arr[l]:
largest = l
# 然后看看右子树是不是存在,并且是不是比当前
# 已有的(可能是父节点可能是左子树的)最大元素大
if r < n and arr[largest] < arr[r]:
largest = r
# 如果最大元素索引不是父节点自己,说明需要换位
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i] # swap
# 换了位置,说明这个父节点的子树元素发生了变化
# 不能保证子树还是最大堆,所以要对这个变化了的位置再进行堆化
heapify(arr, n, largest)
def heapSort(arr):
n = len(arr)
# 搭建最大堆
# 如之前说的,我们从最后一个可能的父节点开始遍历((n//2)-1)
for i in range(n // 2 - 1, -1, -1):
heapify(arr, n, i)
# 到这一步的时候arr已经是个最大堆了(根节点一定是数组中最大的元素)
# 但还没有排好序,所以从后往前遍历,这样可以把最大值交换放到数组最后位
# 交换了之后最后一位一定是有序的,所以我们剔除它,并在剩下的元素中继续堆化
for i in range(n - 1, 0, -1):
arr[i], arr[0] = arr[0], arr[i] # swap
heapify(arr, i, 0)
return arr
arr = [47, 4, 5, 24, 63, 16, 8, 45, 6, 33, 9]
print(heapSort(arr))
- 特性
a. 平均时间复杂度: O ( n l o g n ) O(nlogn) O(nlogn)
b. 最好情况: O ( n l o g n ) O(nlogn) O(nlogn)
c. 最坏情况: O ( n l o g n ) O(nlogn) O(nlogn)
d. 空间复杂度: O ( 1 ) O(1) O(1)
e. 排序方式:In-Place
f. 不稳定
与快排比较:
- 相同数据量下,一般堆排序的数据对比次数比快排多。
- 堆排序时间复杂度稳定,最好最坏都是 O ( n l o g n ) O(nlogn) O(nlogn),但快排最坏是 O ( n 2 ) O(n^2) O(n2)
- 因为堆排序中要对比的数据都不是邻近的,所以对缓存不友好。
计数排序
- 步骤
- 图例
- 代码
- 特性
a. 平均时间复杂度: O ( n + k ) O(n+k) O(n+k)
b. 最好情况: O ( n + k ) O(n+k) O(n+k)
c. 最坏情况: O ( n + k ) O(n+k) O(n+k)
d. 空间复杂度: O ( k ) O(k) O(k)
e. 排序方式:Out-Place
f. 稳定
桶排序
- 步骤
- 图例
- 代码
- 特性
a. 平均时间复杂度: O ( n + k ) O(n+k) O(n+k)
b. 最好情况: O ( n + k ) O(n+k) O(n+k)
c. 最坏情况: O ( n ) O(n) O(n)
d. 空间复杂度: O ( k ) O(k) O(k)
e. 排序方式:Out-Place
f. 稳定
基数排序
- 步骤
- 图例
- 代码
- 特性
a. 平均时间复杂度: O ( n × k ) O(n \times k) O(n×k)
b. 最好情况: O ( n × k ) O(n \times k) O(n×k)
c. 最坏情况: O ( n × k ) O(n \times k) O(n×k)
d. 空间复杂度: O ( n + k ) O(n+k) O(n+k)
e. 排序方式:Out-Place
f. 稳定
常见十个
https://www.cnblogs.com/wuxinyan/p/8615127.html
二叉树
二叉搜索树
二叉搜索树是一种节点值之间具有一定数量级次序的二叉树,对于树中每个节点:
若其左子树存在,则其左子树中每个节点的值都不大于该节点值(左子树节点都小于它);
若其右子树存在,则其右子树中每个节点的值都不小于该节点值(右子树节点都大于它)。
队列
优先队列(Priority Queue)
即有某种优先顺序的队列。一般
- 用python实现最简单的PQ就是利用queue存储,什么都不变,仅仅在delete的时候遍历queue然后输出最大(小)的元素。
class PriorityQueue(object):
def __init__(self):
self.queue = []
def __str__(self):
return ' '.join([str(i) for i in self.queue])
# 检查queue是否为空
def isEmpty(self):
return len(self.queue) == 0
# 直接正常append元素
def insert(self, data):
self.queue.append(data)
# delete 元素的时候遍历queue找到最大值,然后删除
def delete(self):
try:
max = 0
for i in range(len(self.queue)):
if self.queue[i] > self.queue[max]:
max = i
item = self.queue[max]
del self.queue[max]
return item
except IndexError:
print()
exit()
if __name__ == '__main__':
myQueue = PriorityQueue()
myQueue.insert(12)
myQueue.insert(1)
myQueue.insert(14)
myQueue.insert(7)
print(myQueue)
while not myQueue.isEmpty():
print(myQueue.delete())
- 上述方法的时间复杂度为 O ( n ) O(n) O(n),但我们有更快速的方法:二叉堆(Binary Heap),就是前文中的堆排序也有讲到的最大/小堆。
剑指Offer
归纳类型,题目解释,多种做法
Stack&Queue
一般用辅助stack push/pop就可以解决
剑指09
用两个栈实现一个队列。队列的声明如下,请实现它的两个函数 appendTail 和 deleteHead ,分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素,deleteHead 操作返回 -1 )
基本思路:stack1存储,stack2辅助删除。
方法1:自己的拉胯方法。把CQueue完全当成queue来处理,遇到删除时,stack1所有内容反向推给stack2,除了最后一个,然后再从stack2反向推给stack1,维持次序。
时间复杂度:O(n),两次for循环。

方法2:好一点的方法。把两个stack分开看,第一次出现delete,就把stack1的内容反向推给stack2,除了最后一个。这样保证在这次delete之前的内容都已经反向,stack2只要pop就一定是队头。即使在stack2中还有内容时,我们往stack1中append也不影响stack2的delete。
什么时候返回-1,就是在stack2中没有delete了,然后发现stack1中也没内容反推至stack2了。
时间复杂度:O(n),一个循环


代码:
class CQueue:
def __init__(self):
# self 的解释,python的list是个stack
self.stack1 = []
self.stack2 = []
def appendTail(self, value: int) -> None:
# 用stack1维持队列
self.stack1.append(value)
def deleteHead(self) -> int:
# 不是第一次在append之后delete了
if self.stack2:
return self.stack2.pop()
# append之后有过一次delete
if len(self.stack1) == 0:
return -1
# stack2辅助删除头
for i in range(len(self.stack1)):
self.stack2.append(self.stack1.pop())
#head = self.stack2.pop()
#for i in range(len(self.stack2)):
# self.stack1.append(self.stack2.pop())
#return head
return self.stack2.pop()
剑指30
定义栈的数据结构,请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中,调用 min、push 及 pop 的时间复杂度都是 O(1)。
基本思路:一个主要stack存数据,一个辅助栈aux帮助减少找到最小值的时间复杂度。
方法1:第一反应,啥玩意啊,一个min()完事了,O(n)也不错了。
方法2:好吧要O(n)还要我写算法干什么,那就想怎么去除min()的O(n)变成O(1)。
top不用说直接[-1]或者peek()进行返回;push的时候用辅助aux来及记录当前情况下stack的最小值;pop的时候stack正常pop,然后存储此值来和aux最后一个值做对比,看是否pop了当前最小值,是的话aux也要pop;min直接返回aux的最后一个值。


代码:
class MinStack:
def __init__(self):
self.stack = []
self.aux = []
def push(self, x: int) -> None:
self.stack.append(x)
if self.aux:
if self.aux[-1] >= x:
self.aux.append(x)
else:
self.aux.append(x)
def pop(self) -> None:
out = self.stack.pop()
if out == self.aux[-1]:
self.aux.pop()
def top(self) -> int:
return self.stack[-1]
def min(self) -> int:
# O(n)
#return min(self.stack)
return self.aux[-1]
链表
剑指06
输入一个链表的头节点,从尾到头反过来返回每个节点的值(用数组返回)。
方法1:第一反应,还是stack,不用动脑子遍历。正向遍历一遍链表,再pop出来存储输出。两次循环,两个额外lists。
代码1:
class Solution:
def reversePrint(self, head: ListNode) -> List[int]:
if not head:
return []
stack = []
aux = []
while head:
stack.append(head.val)
head = head.next
while stack:
aux.append(stack.pop())
return aux
方法2:突然隐约想起励志做产品前天天在写的递归。重点:递归和stack有相似的特性,先进后出!(下方注释掉的代码为递归)
Base case:当链表为空时,返回[];
Recursion:递归寻找下一个节点,直到找到最后一个时,开始向list里append这个节点的值。
Return:返回list。
TODO:关于递归的时间复杂度可以参考:https://zhuanlan.zhihu.com/p/129887381
代码2:
class Solution:
def reversePrint(self, head: ListNode) -> List[int]:
if not head:
return []
reverse = self.reversePrint(head.next)
reverse.append(head.val)
return reverse
剑指24
定义一个函数,输入一个链表的头节点,反转该链表并输出反转后链表的头节点。
方法1:用了笨办法,遍历将链表值存进stack,然后记录一个新的头节点,挨个pop出stack内元素,并做成节点,最后返回新的头节点。时间复杂度O(n),额外用了一个stack。
代码1:
class Solution:
def reverseList(self, head: ListNode) -> ListNode:
if not head:
return None
stack = []
while head:
stack.append(head.val)
head = head.next
reverse = ListNode(stack.pop())
#涉及到浅拷贝和深拷贝
temp = reverse
while stack:
temp.next = ListNode(stack.pop())
temp = temp.next
return reverse
方法2:双指针法。既然要反转输出,那么就将head的next指向null,然后每一个节点的next都指向自己前面的那个节点。


代码2:
class Solution:
def reverseList(self, head: ListNode) -> ListNode:
if not head:
return None
cur = head
pre = None
while cur:
tmp = cur.next
cur.next = pre
pre = cur
cur = tmp
return pre
剑指35
请实现 copyRandomList 函数,复制一个复杂链表。在复杂链表中,每个节点除了有一个 next 指针指向下一个节点,还有一个 random 指针指向链表中的任意节点或者 null。
解题思路:简单的说就是要把所有的节点深拷贝一下,同样的内容但不同的对象(地址)。
方法1:既然要创建新的对象,那就从头开始,一步步来。先创建新的头,并且将新的头和旧的头做对应记录,然后查看旧头next是否已经访问过了(在对应记录里找),如果没有,那么就创建新头的next/random节点,同样做新旧对应记录;如果有就直接连接到那一点。反复执行直至原链表遍历完成。

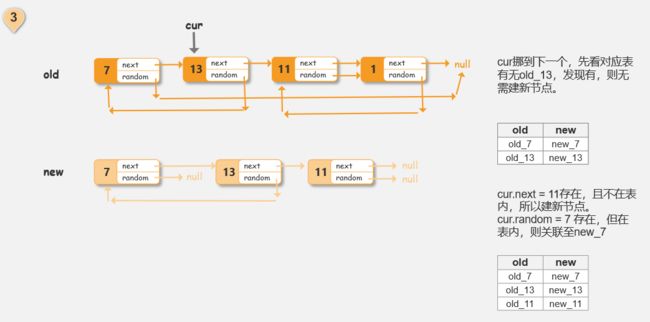
 代码1:
代码1:
class Solution:
# https://leetcode-cn.com/problems/fu-za-lian-biao-de-fu-zhi-lcof/solution/lian-biao-de-shen-kao-bei-by-z1m/
def copyRandomList(self, head: 'Node') -> 'Node':
# Node with label 7 was not copied but a reference to the original one. xswl
# return head
if not head:
return None
# 方法1:
# 生成一个新头,并记录新头
new_head = Node(head.val,None,None)
# 记录一下原Node是否被visited,visited之后他的clone地址是谁
visited = {head:new_head}
# 新头指针
cur = new_head
# 看原头是否有下一个
while head.next:
# next是不是已经存在
if visited.get(head.next):
# 有就记录他的clone地址
clone = visited.get(head.next)
else:
# 没有就建立一个新的
clone = Node(head.next.val,None,None)
visited[head.next]=clone
# 关联next
cur.next = clone
# 再看head的random是谁
# 没random
if not head.random:
cur.random = None
else:
# 有random
# 看random地址存不存在
if visited.get(head.random):
# 存在
cur.random = visited.get(head.random)
else:
# 不存在
cur.random = Node(head.random.val, None, None)
visited[head.random]=cur.random
# 原头向下走
head = head.next
# 更新新指针位置
cur = clone
# 没random
if not head.random:
cur.random = None
else:
# 有random
# 看random地址存不存在
if visited.get(head.random):
# 存在
cur.random = visited.get(head.random)
else:
# 不存在
cur.random = Node(head.random.val, None, None)
visited[head.random]=cur.random
return new_head
方法2:TODO:图的做法
String
剑指 05
请实现一个函数,把字符串 s 中的每个空格替换成"%20"。
方法:啥玩意,直接按字符遍历之后,碰到“ ”就在新的string加上%20,如果不是就加上当前字符。python一个机灵直接s.replace
代码:
class Solution:
def replaceSpace(self, s: str) -> str:
# 笑死个人
# return s.replace(' ','%20')
# 用一个新的string存储结果
out=""
for i in s:
if i!=' ':
out+=i
else:
out+='%20'
return out
剑指58
字符串的左旋转操作是把字符串前面的若干个字符转移到字符串的尾部。请定义一个函数实现字符串左旋转操作的功能。比如,输入字符串"abcdefg"和数字2,该函数将返回左旋转两位得到的结果"cdefgab"。
方法1:。。。直接切片。TODO:不同切片表达以及原理。
代码1:
class Solution:
def reverseLeftWords(self, s: str, n: int) -> str:
return s[n:]+s[0:n]
方法2:不能切片就老实遍历,先遍历n+1到结束并+到string里面,然后再遍历前n个并+到string里。
代码2:
class Solution:
def reverseLeftWords(self, s: str, n: int) -> str:
output=""
for i in range(n,len(s)):
output += s[i]
for i in range(n):
output += s[i]
return output
32-1
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
# https://blog.csdn.net/weixin_43533825/article/details/89155648 Queue
# https://www.cnblogs.com/zhenwei66/p/6598996.html 双向队列
'''
写成前序遍历了
return self.traversal(root,[])
def traversal(self, root, result):
if not root:
return []
result.append(root.val)
self.traversal(root.left,result)
self.traversal(root.right,result)
return result
'''
class Solution:
def levelOrder(self, root: TreeNode) -> List[int]:
if not root:
return []
res = []
queue = collections.deque()
queue.append(root)
while queue:
visited = queue.popleft()
if visited:
res.append(visited.val)
queue.append(visited.left)
queue.append(visited.right)
return res
32-2
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def levelOrder(self, root: TreeNode) -> List[List[int]]:
if not root:
return []
res = []
queue = collections.deque()
queue.append(root)
while queue:
temp = []
aux_queue = collections.deque()
# 看当前queue的长度
for _ in range(len(queue)):
# 一次性把一层的都pop完
visited = queue.popleft()
temp.append(visited.val)
if visited.left:
# 用另一个临时queue来存储子节点
aux_queue.append(visited.left)
if visited.right:
aux_queue.append(visited.right)
queue = aux_queue
res.append(temp)
return res
32-3
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def levelOrder(self, root: TreeNode) -> List[List[int]]:
if not root:
return []
res = []
queue = collections.deque()
queue.append(root)
# 存储正向queue
flag = 1 # 1 表示从左到右,0表示从右到左
while queue:
temp = []
aux_queue = collections.deque()
# 看当前queue的长度
for i in range(len(queue)):
# 一次性把一层的都pop完
if flag == 1:
visited = queue.popleft()
if visited.left:
# 用另一个临时queue来存储子节点
aux_queue.append(visited.left)
if visited.right:
aux_queue.append(visited.right)
else:
visited = queue.pop()
if visited.right:
# 气死我了欺负我不知道appendleft是吧
aux_queue.appendleft(visited.right)
if visited.left:
# 用另一个临时queue来存储子节点
aux_queue.appendleft(visited.left)
temp.append(visited.val)
queue = aux_queue
res.append(temp)
flag = 1 - flag
return res
26
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def isSubStructure(self, A: TreeNode, B: TreeNode) -> bool:
# 两个树有一个是空的而且还没匹配上,那就false
if not B or not A:
return False
return self.recur(A,B) or self.isSubStructure(A.left,B) or self.isSubStructure(A.right,B)
# isSub的目的是找到根节点
# recur的目的就是在找到根节点之后去完成子树匹配
def recur(self,A,B):
# B 空了,说明B遍历完了,
if not B:
return True
# A空了都没匹配上
if not A:
return False
# 两个点值不同
if A.val != B.val:
return False
# 相同,就分别看左边和右边
return self.recur(A.left,B.left) and self.recur(A.right,B.right)
27
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def mirrorTree(self, root: TreeNode) -> TreeNode:
"""
if not root:
return None
# stack和queue一样,只是为了存储原来树的顺序
stack = [root]
while stack:
# 当前节点pop
node = stack.pop()
# stack接着存
if node.left:
stack.append(node.left)
if node.right:
stack.append(node.right)
# 原树进行左右节点交换
node.left, node.right = node.right, node.left
return root
"""
if not root:
return None
# 递归左子树
leftRoot = self.mirrorTree(root.left)
rightRoot = self.mirrorTree(root.right)
# 让左子树为右边
root.left = rightRoot
root.right = leftRoot
return root
28
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
def recur(left,right):
# 两边都为空,则遍历完了
if not left and not right:
return True
if (not left or not right) or (left.val != right.val):
return False
# 然后对比left的left和right的right是否一样,left的right和right的left是否一样
return recur(left.left,right.right) and recur(left.right,right.left)
if not root:
return True
return recur(root.left,root.right)
"""
if not root:
return True
queue = collections.deque()
queue.append(root)
while queue:
aux = collections.deque()
# 如果是根就跳过下面的循环
if len(queue) != 1:
# 如果前后都不是null,则可以比较数值
for i in range(int(len(queue)/2)):
if queue[i] and queue[len(queue)-1-i]:
if queue[i].val != queue[len(queue)-1-i].val:
return False
# 只有一个是null,则不对称
elif (queue[i] and not queue[len(queue)-1-i]) or (not queue[i] and queue[len(queue)-1-i]):
return False
for _ in range(len(queue)):
visited = queue.popleft()
if visited:
aux.append(visited.left)
aux.append(visited.right)
# 奇数的时候一定不是对称的
if len(aux)%2==1:
return False
queue = aux
return True
"""
10-1
class Solution:
def fib(self, n: int) -> int:
if n == 0 or n == 1:
return n
a = 0
b = 1
while n > 1:
n -= 1
c = (a + b)%1000000007
a = b
b = c
return c
# 递归超时
# return (self.fib(n-1)+self.fib(n-2))%1000000007
# 可以理解为a = a1 + b, b = a1+b-b
# a = a + b;
# b = a - b;
10-2
class Solution:
def numWays(self, n: int) -> int:
if n == 0 or n == 1:
return 1
dp = [0]*(n+1)
dp[0] = 1
dp[1] = 1
for i in range(2,n+1):
dp[i] = dp[i-1] + dp[i-2]
dp[i] = dp[i] % 1000000007
return dp[n]
63
class Solution:
def maxProfit(self, prices: List[int]) -> int:
# 不增加额外数组
if len(prices) == 0 or len(prices) == 1:
return 0
cheapest = float("inf")
profit = 0
for price in prices:
cheapest = min(cheapest,price)
profit = max(profit,price-cheapest)
return profit
"""
length = len(prices)
if length == 0 or length == 1:
return 0
dp = [0]*length
mini = prices[0]
for i in range(1,length):
# 维持一个最小的买入价
if mini > prices[i]:
mini = prices[i]
# 看是前一天的收益高,还是当前减去前面最小的收益高
dp[i] = max(dp[i-1],prices[i]-mini)
return dp[length-1]
"""
42
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
# dp两种情况,如果前面的加上自己更大了,则和前面的连为一体
# 如果前面的少,则自己从头再来。
if len(nums) == 1:
return nums[0]
dp = [0]*len(nums)
dp[0] = nums[0]
for i in range(1,len(nums)):
dp[i] = max(dp[i-1]+nums[i],nums[i])
return max(dp)
# 以某个数作为结尾,意思就是这个数一定会加上去,
# 那么要看的就是这个数前面的部分要不要加上去。大于零就加,小于零就舍弃。
47
class Solution:
def maxValue(self, grid: List[List[int]]) -> int:
dp=[[0]*len(grid[0]) for i in range(len(grid))]
# 只有一行
if len(grid) == 1:
sum = 0
for j in range(len(grid[0])):
sum += grid[0][j]
# 只有一列
if len(grid[0]) == 1:
sum = 0
for i in range(len(grid)):
sum += grid[i][0]
return sum
# 先初始化左上角
dp[0][0] = grid[0][0]
# 再初始化第一行和第一列,因为他们只能从左边的或者上面的数字过来
for i in range(1,len(grid[0])):
dp[0][i] = dp[0][i-1] + grid[0][i]
for i in range(1, len(grid)):
dp[i][0] = dp[i-1][0] + grid[i][0]
# 开始正式遍历
for i in range(1,len(grid)):
for j in range(1,len(grid[0])):
# 当前这个点,要么是上面来的,要么是左边来的,看哪边来的大
# 再加上当前的点
dp[i][j] = max(dp[i][j-1],dp[i-1][j]) + grid[i][j]
return dp[-1][-1]
36的nonlocal
"""
# Definition for a Node.
class Node:
def __init__(self, val, left=None, right=None):
self.val = val
self.left = left
self.right = right
"""
class Solution:
def treeToDoublyList(self, root: 'Node') -> 'Node':
pre = head = None
def dfs(cur):
nonlocal pre
nonlocal head
if not cur:
return
dfs(cur.left)
if not pre:
head = pre = cur
else:
pre.right = cur
cur.left = pre
pre = cur
dfs(cur.right)
if not root:
return None
dfs(root)
head.left = pre
pre.right = head
return head
后续主要用两种方法,一个是脑子里第一个弹出来的,第二个是优化的。先过一遍,后续再研究其他方法
函数相关链接:init,-> ↩︎
List相关链接 ↩︎
字典参考链接 ↩︎
哈希表参考链接 ↩︎




