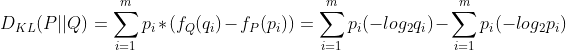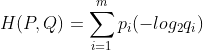信息量、熵、相对熵与交叉熵的理解

一、信息量

信息奠基人香农（Shannon）认为“信息是用来消除随机不确定性的东西”。也就是说衡量信息量大小就看这个信息消除不确定性的程度。

“太阳从东方升起了”这条信息没有减少不确定性。因为太阳肯定从东面升起。这是句废话，信息量为0。

“吐鲁番下中雨了”（吐鲁番年平均降水量日仅6天）这条信息比较有价值，为什么呢，因为按统计来看吐鲁番明天不下雨的概率为98%（1-6/300），对于吐鲁番下不下雨这件事，首先它是随机不去确定的，这条信息直接否定了发生概率为98%的事件------不下雨，把非常大概率的事情（不下雨）否定了，即消除不确定性的程度很大，所以这条信息的信息量比较大。这条信息的情形发生概率仅为2%但是它的信息量去很大，上面太阳从东方升起的发生概率很大为1，但信息量确很小。

从上面两个例子可以看出：信息量的大小和事件发生的概率成反比。

信息量的表示:

二、熵

熵可以衡量一个系统的混乱程度，从信息的角度来说，是从一种定量的角度来衡量信息多少的指标。简单来说，就是信息所包含的不确定性的大小，一个信息所包含的事件的不确定性越大，它所含的信息就越多。熵的本质是香农信息量的期望值。

熵的定义：如果一个随机变量X的可能取值为X = {x1, x2,…, xk}，其概率分布为P(X = xi) = pi（i = 1,2, ..., n），则随机变量X的熵定义为：

H(X)表示X包含的信息，pi表示X第i种可能的概率。

三、衡量两个事件/分布之间的不同：相对熵（KL散度）

比如有两个系统Q和P，事件在两个系统中发生的概率是不一样的。

如果对于这一个事件，用它在系统Q中的信息量-它对应到P中的信息量，这个差值最后求整体的期望，就是它的相对熵。（注意，pi在前面代表以P为基准）

从公式可以看出，如果pi=qi，即两个分部完全相同，那么KL散度为0，还可以看到，这个公式后一部分就是p的信息熵。

而且，KL散度在计算两个分部的时候不是对称的，上面公式的意义就是求P和Q的对数差在P上的期望值。

四、交叉熵

我们从上面KL散度的式子中可以看出，后一部分其实就是P的信息熵，那么前一部分其实就是交换熵。P和Q的交换熵=P和Q的KL散度-P的熵

从名字上看，交叉熵主要用于描述两个事件之间的相互关系，对自己求交叉熵等于熵。

五、为什么可以用交叉熵作为代价函数？

机器学习的过程就是希望在训练数据上学到的分布P(model)和真实分布P(real)越接近越好，最小化两个分布之间的关系就是使其KL散度最小。但我我们没有真实分布，只能退而求其次，希望学到的模型分布P(model)与训练数据的分布P(training)一致。

由此我们需要最小化

P(training)是训练数据集给定的，那么training数据集信息熵也是已知的，求KL散度可以等同于求H(P(training),P(model))。当交叉熵最低时，我们就学到了最好的模型。

参考：(70条消息) 交叉熵与KL散度_达瓦里氏吨吨吨的博客-CSDN博客_kl散度 交叉熵

(70条消息) 熵（entropy）的定义_www_helloworld_com的博客-CSDN博客_熵的定义

(70条消息) 信息量与信息熵_zhengudaoer的博客-CSDN博客_信息量和信息熵