TensorFlow笔记之神经网络优化——损失函数
- 神经元模型:用数学公式表示为
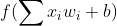 , f 为激活函数。神经网络是以神经元为基本单位构成的。
, f 为激活函数。神经网络是以神经元为基本单位构成的。 - 激活函数:引入非线性激活函数,提高模型的表达力。
常用的激活函数有relu、sigmoid、tanh等。
① relu:在TensorFlow中,用tf.nn.relu()表示
② sigmoid:在TensorFlow中,用tf.nn.sigmoid()表示

③ tanh:在TensorFlow中,用tf.nn.tanh()表示
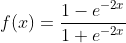
- 损失函数:用来表示预测值(y)与已知答案(y_)的差距。在训练神经网络是,通过不断改变神经网络中所有参数,使损失函数不断减小,从而训练出更高的准确率的神经网络模型。常用的损失函数有均方误差、自定义和交叉熵等。
① 均方误差mse:预测值y与已知答案y_之差的平方和,再求平均值。在TensorFlow中,用loss_mes = tf.reduce_mean(tf.square(y_-y))
例如:
预测酸奶日销量y,x1和x2是影响日销量的两个因素。
应以前采取的数据有:一段时间内,每日的x1因素、x2因素和销量y_。采集的数据尽量多。
在本例中,销量预测产量,最优的产量应该等于销量。由于目前没有数据集,所以拟造了一套数据集。利用TensorFlow中函数随机生成x1、x2,制造表中答案y_ = x1 + x2,为了更真实,求和后还加了正负0.05的随机噪声。#coding:utf-8 #预测多或预测少的影响一样 #0 导入模块,生成数据集 import tensorflow as tf import numpy as np BATCH_SIZE = 8 SEED = 23455 rdm = np.random.RandomState(SEED) X = rdm.rand(32,2) Y = [[x1+x2+(rdm.rand()/10.0-0.05)] for (x1, x2) in X] #1 定义神经网络的输入、参数和输出,定义前向传播过程 x = tf.placeholder(tf.float32, shape=(None, 2)) y_= tf.placeholder(tf.float32, shape=(None, 1)) w1 = tf.Variable(tf.random_normal([2,1], stddev=1, seed=1)) y = tf.matmul(x,w1) #2 定义损失函数及反响传播方法 #定义损失函数为MES,反响传播方法为梯度下降 loss_mes = tf.reduce_mean(tf.square(y_-y)) train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss_mes) #3 生成会话,训练STEPS轮 with tf.Session() as sess: init_op = tf.global_variables_initializer() sess.run(init_op) STEPS = 20000 for i in range(STEPS): start = (i*BATCH_SIZE) % 32 end = start + BATCH_SIZE sess.run(train_step, feed_dict={x:X[start:end], y_:Y[start:end]}) if i % 500 == 0: print "After %d training steps, w1 is: " %i print sess.run(w1) print "Finam w1 is: \n", sess.run(w1) """ Finam w1 is: [[0.98019385] [1.0159807 ]] """可以看到,神经网络模型得到最终参数w1=0.98,w2=1.02,销售预测结果为y=0.98*x1+1.02*x2。由于在生成数据集时,标准答案为y=x1+x2,因此,销售量预测结果和标准答案已经非常接近,说明该神经网络预测酸奶销售量正确。
②自定义损失函数:根据问题的实际情况,定制合理的损失函数。
例如:对于预测酸奶的销售量问题,如果预测销量大于实际销量,则会损失成本;如果预测销量小于实际销量,则会损失例如。在实际生活中,往往制造一盒酸奶的成本和销售一盒酸奶的利润是不等价的。因此,需要使用符合该问题的自定义损失函数。
自定义成分段函数:
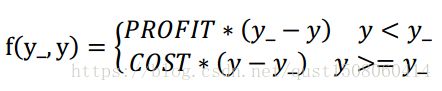
损失函数表示,若预测结果y小于标准答案y_,损失函数为利润乘以预测结果y与标准答案之差;若预测结果y大于标准答案y_,损失函数为成本乘以预测结果y与标准答案y_之差。
用TensorFlow函数表示为:loss_mes = tf.reduce_sum(tf.where(tf.greater(y,y_), (y - y_)*COST, (y_-y)*PROFIT))
若酸奶成本为1元,酸奶销售利润为9元,则制造成本小于酸奶利润,因此,希望预测结果y多一些。采用上述的自定义损失函数,训练神经网络模型。代码如下:
#coding:utf-8 #预测多或预测少的影响一样 #0 导入模块,生成数据集 import tensorflow as tf import numpy as np BATCH_SIZE = 8 SEED = 23455 COST = 1 PROFIT = 9 rdm = np.random.RandomState(SEED) X = rdm.rand(32,2) Y = [[x1+x2+(rdm.rand()/10.0-0.05)] for (x1, x2) in X] #1 定义神经网络的输入、参数和输出,定义前向传播过程 x = tf.placeholder(tf.float32, shape=(None, 2)) y_= tf.placeholder(tf.float32, shape=(None, 1)) w1 = tf.Variable(tf.random_normal([2,1], stddev=1, seed=1)) y = tf.matmul(x,w1) #2 定义损失函数及反响传播方法 #定义损失函数为MES,反响传播方法为梯度下降 loss_mes = tf.reduce_sum(tf.where(tf.greater(y,y_), (y - y_)*COST, (y_-y)*PROFIT)) train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss_mes) #3 生成会话,训练STEPS轮 with tf.Session() as sess: init_op = tf.global_variables_initializer() sess.run(init_op) STEPS = 20000 for i in range(STEPS): start = (i*BATCH_SIZE) % 32 end = start + BATCH_SIZE sess.run(train_step, feed_dict={x:X[start:end], y_:Y[start:end]}) if i % 500 == 0: print "After %d training steps, w1 is: " %i print sess.run(w1) print "Finam w1 is: \n", sess.run(w1) """ Final w1 is: [[1.020171 ] [1.0425103]] """若成本为9元,利润为一元,只需更改COST和PROFIT的值即可。运行结果如下:
""" Final w1 is: [[0.9661967 ] [0.97694933]] """③交叉熵:表示两个概率分布之间的距离。交叉熵越大,两个概率分布之间的距离越远,连个概率分布越相异;交叉熵越小,两个概率分布距离越近,两个概率分布越相似。
交叉熵计算公式: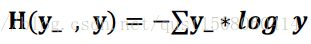
用TensorFlow函数表示为:ce= -tf.reduce_mean(y_* tf.log(tf.clip_by_value(y, 1e-12, 1.0)))
例如:两个神经网络模型解决二分类问题中,已知标准答案为 y_ = (1, 0),第一个神经网络模型预测结果为
y1=(0.6, 0.4),第二个神经网络模型预测结果为 y2=(0.8, 0.2),判断哪个神经网络模型预测的结果更接
近标准答案。
根据交叉熵的计算公式得:
H1((1,0),(0.6,0.4)) = -(1*log0.6 + 0*log0.4) ≈ -(-0.222 + 0) = 0.222
H2((1,0),(0.8,0.2)) = -(1*log0.8 + 0*log0.2) ≈ -(-0.097 + 0) = 0.097
由于 0.222>0.097,所以预测结果 y2 与标准答案 y_更接近, y2 预测更准确。
④softmax函数:将n分类的n个输出(y1,y2,...,yn)变为满足以下概率分布要求的函数。

softmax函数表示为: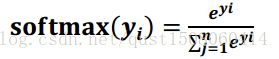
softmax函数应用:在n分类中,模型会有n个输出,即y1,y2,...,yn,其中 yi 表示第 i 种情况出现的可能性大小。将 n 个输出经过softmax函数,课得到符合概率分布的分类结果。
【实际运用】在Tensorflow中,一般让模型的输出经过softmax函数,以获得输出分类的概率分布,再与标准答案对比,求出交叉熵,得到损失函数,用余下函数实现:
ce = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=y, labels=tf.argmax(y_, 1)) cem = tf.reduce_mean(ce