实现单层神经网络

在前面，我们分别使用逻辑回归和 softmax 回归实现了对鸢尾花数据集的分类，逻辑回归能够实现线性二分类的任务，他其实就是最简单的神经网络——感知机。

而softmax回归则实现的是多分类任务，它也可以看做是输出层有多个神经元的单层神经网络。

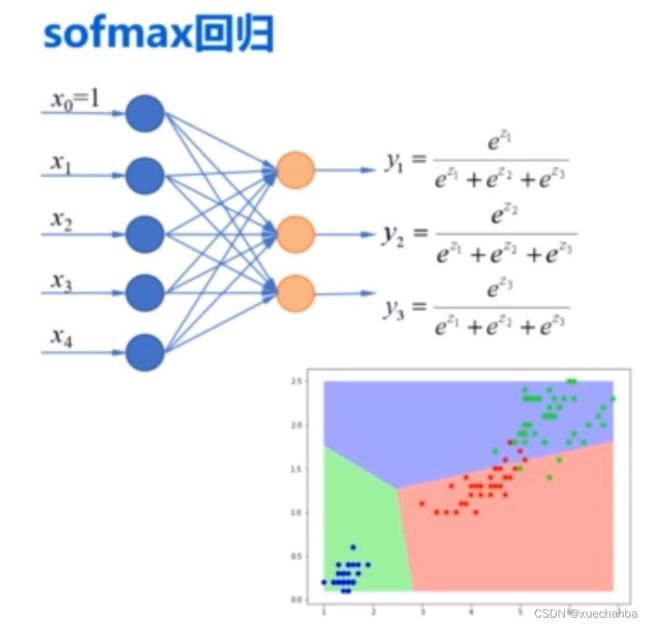
下面，使用神经网络的思想来实现对鸢尾花数据集的分类，这个程序的实现过程和 softmax 回归几乎是完全一样的。

在使用神经网络来解决分类问题时，

首先，要设计神经网络的结构（也就是说确定神经网络有几层，每一层中有几个结点，结点之间又是如何连接的，使用什么激活函数，以及什么损失函数）。

这里，使用没有隐含层的单层前馈型神经网络来实现对鸢尾花的分类。

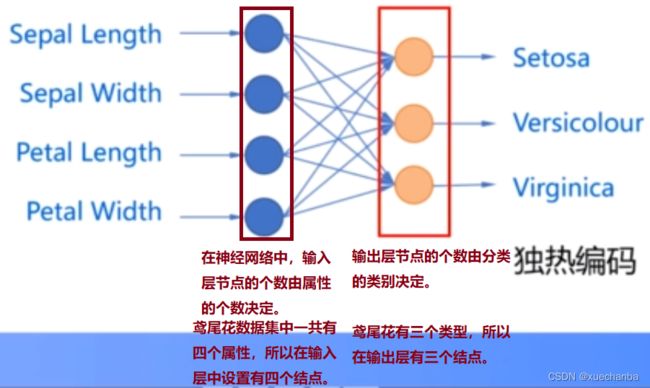
其次，编程来实现，

神经网络是一种数学模型，这些结点和结点之间的关系描述的是数学运算，因此实现神经网络实际就是通过多维数组实现这些数学运算。

在鸢尾花数据集的训练集中，一共有120个样本，如果我们一次输入所有样本，那么输入数据 X 就是一个形状为（120，4）的二维数组（为训练样本的属性值），输出层外是一个形状为（120，3）的二维数组（为对训练样本分类后的标签值）。

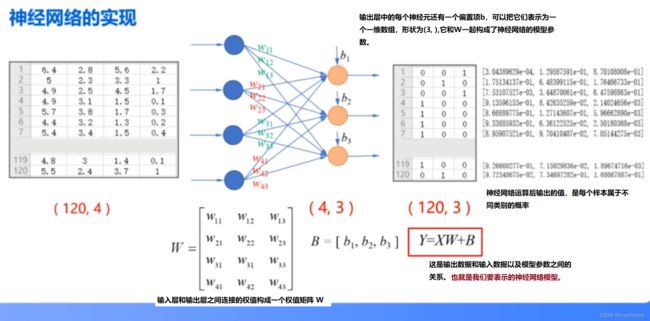
在前面的分类实现中，为了简化编程，我们将偏置项B看做是w₀，将权值向量构造为m+1维的 W 矩阵，并且令 x₀ 为全一数组。将 X 向量构造为 m+1 列。

将这两个矩阵直接运算，

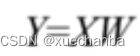
可以得到同样的结果。

在这个实验中，我们将 B 从 W 中分离出来，单独表示，这是考虑到后面实现多层神经网络时，编程更加方便直观。

下面，来介绍下实现神经网络的几个函数：

# 1、softmax
tf.nn.softmax(tf.matmul(X_train, W)+b)  # Y = XW+B

# 2、独热编码 one_hot
tf.one_hot(indices, depth)
# 参数 indices 要求是一个整数, 是一个输入项
# 参数 depth 是独热编码的深度

# 将鸢尾花数据集中的标签值转化为用独热编码表示
# 鸢尾花数据集中的标签值是一个浮点数,所以首先要转换为整数
tf.one_hot(tf.constant(y_test, dtype=tf.int32), 3)

# 3、交叉熵损失函数 tf.keras.losses.categorical_crossentropy
tf.keras.losses.categorical_crossentropy(y_true, y_pred)
# 第一个参数表示为独热编码的标签值
# 第二个参数是softmax函数的输出
# 返回值是一个一维张量
# 其中的每一个元素是每个样本的交叉熵损失值
# 因此, 还需要使用平均值函数得到平均交叉熵损失值
tf.reduce_mean(tf.keras.losses.categorical_crossentropy(y_true=Y_train, y_pred=Y_PRED_train))
# 或使用求和函数得到总的交叉熵损失值
tf.reduce_sum(tf.keras.losses.categorical_crossentropy(y_true=Y_train, y_pred=Y_PRED_train))

完整的程序实现

目标：利用单层神经网络实现对鸢尾花数据集的分类

import pandas as pd
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = "SimHei"
plt.rcParams['axes.unicode_minus'] = False

# 目标：使用花萼长度、花萼宽度、花瓣长度、花瓣宽度四种属性将三种鸢尾花区分开

# 第一步：加载数据集
TRAIN_URL = "http://download.tensorflow.org/data/iris_training.csv"
train_path = tf.keras.utils.get_file(TRAIN_URL.split('/')[-1], TRAIN_URL)
df_iris_train = pd.read_csv(train_path, header=0)  # 表示第一行数据作为列标题

TEST_URL = "http://download.tensorflow.org/data/iris_test.csv"
test_path = tf.keras.utils.get_file(TEST_URL.split('/')[-1], TEST_URL)
df_iris_test = pd.read_csv(test_path, header=0)

# 第二步：数据处理
# 2.1 转化为NumPy数组
iris_train = np.array(df_iris_train)  # 将二维数据表转换为 Numpy 数组, (120, 5), iris的训练集中有120条样本,
iris_test = np.array(df_iris_test)  # 将二维数据表转换为 Numpy 数组, (30, 5), iris的测试集中有30条样本,

# 2.2 提取属性和标签
train_x = iris_train[:, 0:4]  # 取出鸢尾花训练数据集中属性列
train_y = iris_train[:, 4]  # 取出最后一列作为标签值, (120,)

test_x = iris_test[:, 0:4]  # 取出鸢尾花训练数据集中属性列
test_y = iris_test[:, 4]  # 取出最后一列作为标签值, (30, )

# 2.3 数据归一化
# 可以看出这两个属性的尺寸相同,因此不需要进行归一化,可以直接对其进行中心化处理
# 对每个属性进行中心化, 也就是按列中心化, 所以使用下面这种方式
train_x = train_x - np.mean(train_x, axis=0)
test_x = test_x - np.mean(test_x, axis=0)
# 此时样本点的横坐标和纵坐标的均值都是0

# 鸢尾花数据集中的属性值和标签值都是64位的浮点数
print(train_x.dtype)  # float64
print(train_y.dtype)  # float64

# 2.4 生成多元模型的属性矩阵和标签列向量
X_train = tf.cast(train_x, tf.float32)
# 创建张量函数tf.constant()
Y_train = tf.one_hot(tf.constant(train_y, dtype=tf.int32), 3)  # 将标签值转换为独热编码的形式
print(X_train.shape)  # (120, 4)
print(Y_train.shape)  # (120, 3)

X_test = tf.cast(test_x, tf.float32)
# 创建张量函数tf.constant()
Y_test = tf.one_hot(tf.constant(test_y, dtype=tf.int32), 3)  # 将标签值转换为独热编码的形式
print(X_test.shape)  # (30, 4)
print(Y_test.shape)  # (30, 3)

# 第三步：设置超参数和显示间隔
learn_rate = 0.2
itar = 500

display_step = 100

# 第四步：设置模型参数初始值
np.random.seed(612)
# 这里的W是一个(4, 3) 的矩阵
W = tf.Variable(np.random.randn(4, 3), dtype=tf.float32)
# 这里的B是一个(3, ) 的一维张量, 初始化为0
B = tf.Variable(np.zeros([3]), dtype=tf.float32)

# 第五步：训练模型
cross_train = []  # 列表cross_train用来保存每一次迭代的交叉熵损失
acc_train = []  # 用来存放训练集的分类准确率

cross_test = []  # 列表cross_test用来保存每一次迭代的交叉熵损失
acc_test = []  # 用来存放测试集的分类准确率

for i in range(0, itar + 1):

    with tf.GradientTape() as tape:

        # softmax 函数
        # X - (120, 4), W - (4, 3) , 所以 Pred_train - (120, 3), 是每个样本的预测概率
        Pred_train = tf.nn.softmax(tf.matmul(X_train, W) + B)
        # 计算训练集的平均交叉熵损失函数
        Loss_train = tf.reduce_mean(tf.keras.losses.categorical_crossentropy(y_true=Y_train, y_pred=Pred_train))

    Pred_test = tf.nn.softmax(tf.matmul(X_test, W) + B)
    # 计算测试集的平均交叉熵损失函数
    Loss_test = tf.reduce_mean(tf.keras.losses.categorical_crossentropy(y_true=Y_test, y_pred=Pred_test))

    # 计算准确率函数 -- 因为不需要对其进行求导运算, 因此也可以把这条语句写在 with 语句的外面
    Accuarcy_train = tf.reduce_mean(tf.cast(tf.equal(tf.argmax(Pred_train.numpy(), axis=1), train_y), tf.float32))
    Accuarcy_test = tf.reduce_mean(tf.cast(tf.equal(tf.argmax(Pred_test.numpy(), axis=1), test_y), tf.float32))

    # 记录每一次迭代的交叉熵损失和准确率
    cross_train.append(Loss_train)
    cross_test.append(Loss_test)
    acc_train.append(Accuarcy_train)
    acc_test.append(Accuarcy_test)

    # 对交叉熵损失函数 W 和 B 求偏导
    grads = tape.gradient(Loss_train, [W, B])
    # 函数assign_sub的作用是实现 Variable 变量的减法赋值
    # 更新模型参数 W
    W.assign_sub(learn_rate * grads[0])  # grads[0] 是 dL_dw, 形状为(4,3)
    # 更新模型偏置项参数 B
    B.assign_sub(learn_rate * grads[1])  # grads[1] 是 dL_db, 形状为(3, )

    if i % display_step == 0:
        print("i: %i, TrainLoss: %f, TrainAccuracy: %f, TestLoss: %f, TestAccuracy: %f"
              % (i, Loss_train, Accuarcy_train, Loss_test, Accuarcy_test))

"""
i: 0, TrainLoss: 2.066978, TrainAccuracy: 0.333333, TestLoss: 1.880855, TestAccuracy: 0.266667
i: 100, TrainLoss: 0.223813, TrainAccuracy: 0.933333, TestLoss: 0.280151, TestAccuracy: 0.933333
i: 200, TrainLoss: 0.171492, TrainAccuracy: 0.950000, TestLoss: 0.200843, TestAccuracy: 0.966667
i: 300, TrainLoss: 0.144387, TrainAccuracy: 0.958333, TestLoss: 0.161774, TestAccuracy: 0.966667
i: 400, TrainLoss: 0.127350, TrainAccuracy: 0.966667, TestLoss: 0.137980, TestAccuracy: 0.966667
i: 500, TrainLoss: 0.115541, TrainAccuracy: 0.966667, TestLoss: 0.121931, TestAccuracy: 0.966667
"""
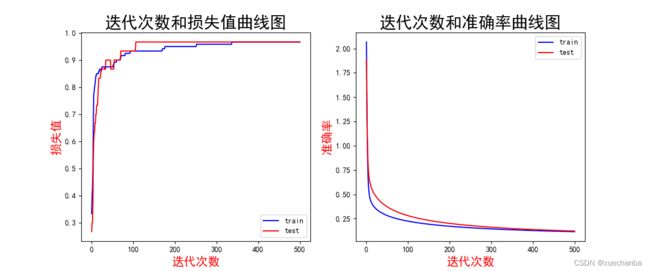
# 第六步：数据可视化
plt.figure(figsize=(12, 5))
plt.subplot(121)
plt.plot(acc_train, color="blue", label="train")
plt.plot(acc_test, color="red", label="test")
plt.title("迭代次数和损失值曲线图", fontsize=22)
plt.xlabel('迭代次数', color='r', fontsize=16)
plt.ylabel('损失值', color='r', fontsize=16)
plt.legend()

plt.subplot(122)
plt.plot(cross_train, color="blue", label="train")
plt.plot(cross_test, color="red", label="test")
plt.title("迭代次数和准确率曲线图", fontsize=22)
plt.xlabel('迭代次数', color='r', fontsize=16)
plt.ylabel('准确率', color='r', fontsize=16)
plt.legend()

plt.show()

运行结果如下：