牛客小白月赛27 题解

比赛时有点事，赛后补了一下题

A 巨木之森
题意就不复述了， 这题的核心内容就是树的直径。
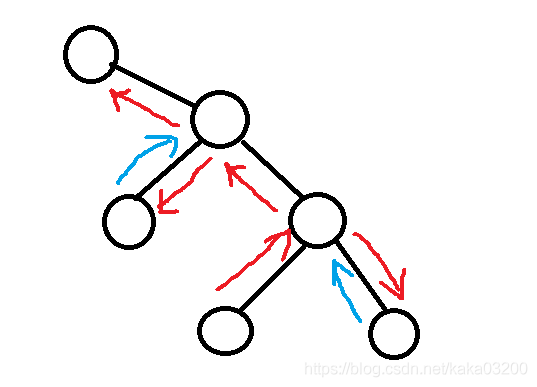
观察下面的图可以发现，一个点遍历整棵树的路程就是 所有的边*2 - 从这个点出发所到的最远距离。根据树的直径的性质，我们可以找到离所有点最远的两个点，然后就是简单的贪心问题了。

#include 
using namespace std;
typedef long long ll;
const int N = 1e5 + 5;

ll dis1[N], dis2[N], m, ans[N], sum, res;

struct edge {
	int to, next, vi;
}e[N<<1];

int n, h[N], cnt, p, q;

void add(int u, int v, int w) {
	e[cnt].to = v;
	e[cnt].vi = w;
	e[cnt].next = h[u];
	h[u] = cnt++;
}

void dfs1(int u, int fa) {
	if (dis1[p] < dis1[u]) p = u;
	for (int i = h[u]; ~i; i = e[i].next) {
		int v = e[i].to;
		if (v == fa) continue;
		dis1[v] = dis1[u] + e[i].vi;
		dfs1(v, u);
	}
}

void dfs2(int u, int fa) {
	if (dis2[q] < dis2[u]) q = u;
	for (int i = h[u]; ~i; i = e[i].next) {
		int v = e[i].to;
		if (v == fa) continue;
		dis2[v] = dis2[u] + e[i].vi;
		dfs2(v, u);
	}
}

int main() {
	memset(h, -1, sizeof h);
	scanf("%d %lld", &n, &m);
	for (int i = 1; i <= n - 1; i++) {
		int x, y, z;
		scanf("%d %d %d", &x, &y, &z);
		add(x, y, z), add(y, x, z);
		sum += z;
	}
	dfs1(1, 0);
	dfs2(p, 0);// p到个点的距离
	dis1[q] = 0;
	dfs1(q, 0);// q到个点的距离
	
	for (int i = 1; i <= n; i++) {
		ans[i] = sum * 2 - max(dis1[i], dis2[i]);
	}
	sort(ans + 1, ans + n + 1);
	if (m < ans[1]) {
		printf("0\n");
		return 0;
	}
	for (int i = 1; i <= n; i++) {
		res += ans[i];
		if (res > m) {
			printf("%d\n", i-1);
			return 0;
		}
	}
	printf("%d\n", n);
}

B 乐团派对
这题有两种解法，一种是贪心，一种是dp
贪心的思路是，从小到大贪心，提前先处理好最后一个最大的数，然后枚举乐队的数量即可。

#include 
using namespace std;
typedef long long ll;
const int N = 1e5 + 10;
const int mod = 1e9;

int n, sum;
int a[N];

int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i];
	sort(a + 1, a + n + 1);
	if (a[n] > n)puts("-1");
	else {
		int r = n - a[n];
		int num = 0;
		sum = 1;
		for (int i = 1; i <= r; i++) {
			num++;
			if (num >= a[i]) {
				num = 0;
				sum++;
			}
		}
		printf("%d\n", sum);
	}
}

dp的思路是，我们设dp[i]表示前i个人最多可以组成多少乐队，当i > a[i] 时，我们可以将第i个人丢掉，让他们自己组成乐队，然后再加上i-a[i]个人最多组成的乐队数，当然，我们也可以把第i个人放入当前的乐队中。

#include 
using namespace std;
typedef long long ll;
const int N = 1e5 + 10;
const int Mod = 1e9;
int n, a[N], dp[N];
int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i];
	sort(a + 1, a + n + 1);
	if (a[n] > n) {
		printf("-1\n");
		return 0;
	}
	for (int i = 1; i <= n; i++) {
		if (i >= a[i]) dp[i] = max(dp[i - a[i]] + 1, dp[i - 1]);
		else dp[i] = 0;
	}
	printf("%d", dp[n]);
}

C 光玉小镇
状压dp 咕咕咕

D 巅峰对决
维护区间问题，自然想到线段树的模型
题中的区间没有重复的值，因此如果区间内的数是连续的，那么可以通过比较区间的最大最小值之差和区间定义域之差是否相等就可以了。

#include 
using namespace std;
typedef long long ll;
const int N = 1e5 + 5;
int a[N];

struct SegementTree {
	int l, r;
	 int max_, min_;
}t[N * 4];

int n, m;

void push_up(int u) {
	t[u].max_ = max(t[u << 1].max_, t[u << 1 | 1].max_);
	t[u].min_ = min(t[u << 1].min_, t[u << 1 | 1].min_);
}

void build(int l, int r, int u) {
	t[u].l = l, t[u].r = r;
	t[u].max_ = 0, t[u].min_ = 0x3f3f3f3f;
	if (l == r) {
		t[u].max_ = a[l];
		t[u].min_ = a[l];
		return;
	}
	int mid = (l + r) >> 1;
	build(l, mid, u << 1);
	build(mid + 1, r, u << 1 | 1);
	push_up(u);
}

void update(int u, int pos, ll v) {
	if (t[u].l == t[u].r) {
		t[u].min_ = v;
		t[u].max_ = v;
		return;
	}
	int mid = (t[u].l + t[u].r) >> 1;
	if (pos <= mid) update(u << 1, pos, v);
	else update(u << 1 | 1, pos, v);
	push_up(u);
}

int query_min(int ql, int qr, int u) {
	if (ql <= t[u].l && t[u].r <= qr) {
		return t[u].min_;
	}
	
	int mid = (t[u].l + t[u].r) >> 1;
	int res = 0x3f3f3f3f;
	if (ql <= mid) res = min(res, query_min(ql, qr, u << 1));
	if (qr > mid) res = min(res, query_min(ql, qr, u << 1 | 1));
	return res;
}

int query_max(int ql, int qr, int u) {
	if (ql <= t[u].l && t[u].r <= qr) {
		return t[u].max_;
	}

	int mid = (t[u].l + t[u].r) >> 1;
	int res = 0;
	if (ql <= mid) res = max(res, query_max(ql, qr, u << 1));
	if (qr > mid) res = max(res, query_max(ql, qr, u << 1 | 1));
	return res;
}

int main() {
	ios::sync_with_stdio(0);
	cin >> n >> m;
	for (int i = 1; i <= n; i++) cin >> a[i];
	build(1, n, 1);
	while (m--) {
		int op, x, y;
		ll k;
		cin >> op >> x >> y;
		if (op == 1) {
			update(1, x, y);
		}
		else {
			int max_ = query_max(x, y, 1);
			int min_ = query_min(x, y, 1);
			if (y - x == max_ - min_) puts("YES");
			else puts("NO");
		}
	}
}

E 使徒袭来
纯签到，没什么好说的

#include 
using namespace std;
int n;
int main() {
	cin >> n;
	double l = 0, r = 1e9, mid;
	while (r - l > 1e-8) {
		mid = (l + r) * 0.5;
		if (mid * mid * mid < n) l = mid;
		else r = mid;
	}
	printf("%.3lf", 3 * mid);
}

F 核弹剑仙

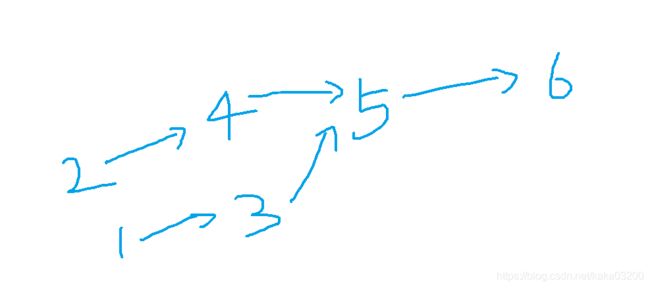
稍微画一下图（略丑），用强的指向弱的，因此题目问有多少强于i的，其实就是有多少能到i的点
题目没有排除重边的可能，因此要用vis处理每个点只经过一次

#include 
using namespace std;
const int N = 1e3 + 10;
vector<int> g[N];
int n, m;
int cnt[N], vis[N];
void dfs(int x) {
	cnt[x]++; vis[x] = 1;
	for (auto v : g[x]) {
        if (!vis[v])
		    dfs(v);
	}
}

int main() {
	ios::sync_with_stdio(0);
	cin >> n >> m;
	for (int i = 1; i <= m; i++) {
		int x, y;
		cin >> x >> y;
		g[x].push_back(y);
	}
	for (int i = 1; i <= n; i++) {
        memset(vis, 0, sizeof vis);
		dfs(i);
	}
	for (int i = 1; i <= n; i++) printf("%d\n", cnt[i]-1);
}

G 虚空之力
也是签到题

组合问题， 能用kinging就用， 剩下的用king
（开始还以为要连续的…kmp 哈希wa了好几发）

#include 
using namespace std;
const int N = 1e7 + 10;
int n;
char str[N];
int k_, i_, n_, g_;
int main() {
	cin >> n;
	cin >> str;
	for (int i = 0; i < n; i++) {
		if (str[i] == 'k') k_++;
		else if (str[i] == 'i') i_++;
		else if (str[i] == 'n') n_++;
		else if (str[i] == 'g') g_++;
	}
	int sum = 0;
	int min_ = min(min(i_, n_), g_);
	if (k_ * 2 < min_) {
		sum += k_ * 2;
	}
	else {
		sum += min_ / 2 * 2;
		i_ -= min_ / 2*2;
		n_ -= min_ / 2*2;
		g_ -= min_ / 2*2;
		k_ -= min_ / 2;
		sum += min(min(min(g_, i_), n_), k_);
	}
	printf("%d", sum);
}

H 社团游戏
处理一下二维前缀和
用sum[i][j][k]表示到第i行第j列有多少个k字符
再用二分取正方形的边长, 并依次判断26个字符
复杂度在500* 500 * 26 *log500左右

#include 
using namespace std;
const int N = 510;
int sum[N][N][27];
char c;
int main() {
	ios::sync_with_stdio(0);
	int n, m, k;
	cin >> n >> m >> k;
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++) {
			cin >> c;
			sum[i][j][c - 'a' + 1] = 1;
		}
	for (int k = 1; k <= 26; k++)
		for (int i = 1; i <= n; i++)
			for (int j = 1; j <= m; j++)

				sum[i][j][k] += sum[i - 1][j][k] + sum[i][j - 1][k] - sum[i - 1][j - 1][k];

	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			int l = 1, r = min(n - i + 1, m - j + 1);
			while (l <= r) {
				int mid = (l + r) >> 1; int f = 0;
				for (int o = 1; o <= 26; o++) {
					if (sum[i + mid - 1][j + mid - 1][o] - sum[i + mid - 1][j - 1][o] - sum[i - 1][j + mid - 1][o] + sum[i - 1][j - 1][o] > k) {
						f = 1;
						break;
					}
				}
				if (f) r = mid - 1;
				else l = mid + 1;
			}
			printf("%d ", r);
		}
		puts("");
	}

}

I 名作之壁
我们可以先固定左端点l，然后用两个单调队列维护区间的最大最小值，如果满足差大于k，那么[l, R], R ∈[r, n]这段区间内的都能满足，因此答案累加n-i+1，然后再将左端向右移动一个单位

#include 
using namespace std;
typedef long long ll;
const int N = 1e7 + 10;
const int Mod = 1e9;

int n, k;
ll a[N], b, c;
ll qMax[N], qMin[N];
ll ans, l;

int main() {
	scanf("%d %d", &n, &k);
	scanf("%lld %lld %lld", &a[0], &b, &c);
	int l1 = 1, l2 = 1, r1 = 0, r2 = 0;
	l = 1;
	for (int i = 1; i <= n; i++) {
		a[i] = (a[i - 1] * b % Mod + c) % Mod;
		while (l1 <= r1 && a[qMax[r1]] <= a[i]) r1--;
		while (l2 <= r2 && a[qMin[r2]] >= a[i]) r2--;
		qMax[++r1] = qMin[++r2] = i;
		//cout << a[qMax[l1]] << " " << a[qMin[l2]] << endl;
		while (a[qMax[l1]] - a[qMin[l2]] > k) {
			ans += 1ll*(n - i + 1);
			l++;
			if (qMax[l1] < l) l1++;
			if (qMin[l2] < l) l2++;
		}
	}
	printf("%lld\n", ans);
}

J 逃跑路线
签到题

#include 
using namespace std;
const int N = 1e5 + 10;
int n, a[N];
int main() {
	cin >> n;
	int ji = 0, ou = 0;
	while (n--) {
		string s;
		cin >> s;
		if ((s[s.size() - 1] - '0') % 2 == 0) ou++;
		else ji++;
	}
	if (ji % 2 == 1) puts("1");
	else puts("0");
}

又水了一篇， ﾚ(ﾟ∀ﾟ;)ﾍ=3=3=3