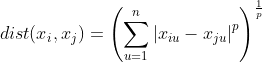典型聚类——K-means算法原理及python实战
1 聚类算法简要介绍
1.1 聚类是什么
聚类是机器学习中的一种重要的无监督算法，可以将数据点归为一系列的特定组合。聚类算法可以将数据点聚成不同的类，揭示数据集中蕴含的不为人知的规律，从而指导我们的生产和生活。简单地说，聚类就是将对象进行分组，使得相似的对象归为一类。对于聚类其实我们并不陌生，我们常说的“物以类聚，人以群分”指的就是聚类。
1.2 聚类算法的应用场景
当聚类作为一个单独的过程时，用来寻找数据本身所蕴含的“分布结构”规律。例如，可以应用聚类结合已知的移动客户所在位置数据为连锁餐饮机新店选址提供参考。
聚类也可以为有监督学习做数据的前期准备，也可以用来为后期对数据做进一步细分。
2 通俗地讲聚类算法的过程
聚类算法是无监督学习的典型算法，其中K-means算法又是其中最经典的算法。K-means算法要求预先设定聚类的个数K，然后不断更新聚类中心，通过多次迭代直至算法收敛或者达到某一个预设的阀值。K-means算法的过程可以简单总结如下：
（1）从含有n个点的数据集中任意选择K个对象作为初始聚类中心。
（2）根据（1）中设置的K个聚类中心，计算每一数据点到这K个中心的距离。
（3）通过步骤（2）的距离计算了以后，每一个数据点与这K个聚类中心都有有一个距离值。这些距离有远的有近的，将数据点与距离它最近的聚类中心归为一类。
（4）通过（3）了以后，数据集被划分成了K个类簇。
（5）重复步骤（3）和步骤（4），不断迭代直至归类趋于稳定或者分类变化量较小时，停止迭代。
2.1 相似度通过距离来度量
聚类就是按照数据的相似度将其划分为多个类别，使得类别内部数据相似度较大而类别间相似度较小。这个“相似度”就是通过距离来进行表示。距离越大，相似度越小，距离越小，相似度越大。最常见的距离是“闵可夫斯基距离”：
(1)当
时，闵可夫斯基不等式就是高中数学中的距离，即欧式距离。
（2）当
时，闵可夫斯基不等式就是曼哈顿距离。
（3）当
时，闵可夫斯基不等式就是切比雪夫距离。
2.2 聚类的性能如何进行度量？
对于性能的评估，下面介绍两种方法：
（1）数据集含有标签信息。有时候虽然数据含有标签信息，也就是说原始数据含有正确的分类信息。但是仍然将数据聚类的时候，就可以考虑使用调整兰德系数（ARI）指标。ARI指标和有监督学习中的准确率比较类似，在sklearn模块中的metrics中就可以调用。
（2）数据不含有标签信息。如果数据集不含有所属类别信息，那么可以考虑使用轮廓系数来评估聚类效果，关于轮廓系数，在下文中会有进一步的介绍。一般来说，轮廓系数越大，聚类效果越好。轮廓系数可以在sklearn模块的metrics中调用silhouette_score来实现。
2.3 具体算法介绍：K-means算法
K-means算法是聚类算法中最简单、最常用的一种，其算法过程如下：
（1）随机选取数据集中的K个初始点作为聚类中心。
（2）为数据集中的每一个点寻找（1）中最近的聚类中心，数据集距离哪个中心最近就把数据集分配到该聚类中心对应的簇。
（3）通过过程（2）了以后，原始数据集被划分成了K个类簇。这个时候，计算每一个类簇的均值并将此均值作为新的聚类中心。
（4）转到步骤（2）和步骤（3）一直到聚类中心不变或者变化很小时停止。
K-means算法中的K个初始聚类中心是随机选取的，一个自然的问题是，不同的初始聚类中心会不会影响最终得到的聚类结果呢？答案是肯定的。在实际问题中，比较合理的是依据具体的实际问题选取合理的K值。
仔细想一想K-means算法过程，随机选取K个点作为初始聚类中心的确会对聚类结果产生影响，这也是K-means算法的缺陷。为此K-means++算法对此问题作了改进。
2.4 具体算法介绍：K-means++算法
针对K-means算法随机选取K个初始点的问题，戴维等人于2007年提出了K++算法。K-means++解决这一个问题的核心思想是，初始聚类中心并不是随机选取，而是希望这K个初始聚类中心分得越开越好。整个算法过程如下：
（1）随机选取一个初始点作为第一个聚类中心，为了叙述的方便，记为点A。
（2）首先计算除了A点以外的所有数据点与A点的距离，记为
，如果数据集包含有n个点，那么得到的距离值就应该有n-1个。接下来，剩下的这n-1个点作为下一个聚类中心的概率
。
（2）' 计算每一个数据点与当下已有聚类中心中隔着自己最近的那个聚类中心的距离(在初始时候，聚类中心只有A点，做的是步骤（2）)。接着计算数据点被选用为下一个聚类中心的概率P（P的计算在（2）中已经给出）
（3）用轮盘法选出下一个聚类中心。（何为轮盘法，后面会说）
（4）重复步骤（2）'和（3）直至选出K个聚类中心。
（5）K个聚类中心选出来了以后，就可以用经典的K-means算法了。
下面，采用一个简单的例子来熟悉上述过程：
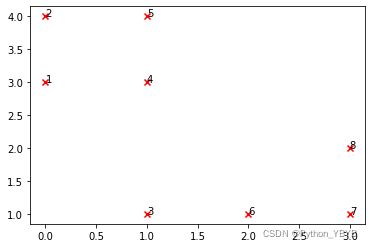
假设我们有一个数据集，为了方便采用二维的点集，数据集中共有8个样本，如下图所示：
首先是随机选取一个初始聚类中心，我们不妨选择1号点，那么选取第二个聚类中心的计算过程如下表所示：
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |  |
|
0 |  |
 |
|
 |
 |
 |
 |
|
 |
0 |  |
 |
|
 |
 |
 |
 |
 |
 |
0 |  |
 |
|
 |
 |
 |
0.314 | |
 |
0 | |
 |
 |
 |
 |
 |
 |
其中，表示数据与初始选的第一个聚类中心1号点的距离，表示数据点被选为下一个聚类中心的概率，是概率的累计值。用轮盘法选出下一个聚类中心：
首先为每一个数据点确定一个其所在的区间，例如2号点所在的区间为[0.034,0.102)，3号点所在的区间为[0.102,0.136),4号点所在的区间为[0.136,0.178),这样确定下去。接下来产生一个0~1之间的一个随机数，随机数在哪个区间中，就选取对应的哪个数据点作为第二个聚类中心。
当完成K个聚类中心的选取了以后，就可以使用经典的K-means算法了。
3 机器学习库sklearn实战——K-means算法
为了方便，使用sklearn.datasets.make_blobs()生成聚类所需要的数据。make.blobs（）函数可以根据指定的特征变量数量类簇聚类中心数量等参数生成指定类别的数据，用于测试聚类算法的效果，make.blobs（）的参数声明可查询有关的资料。
首先导入所需要用到的包：
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
from matplotlib.font_manager import FontProperties
使用make_blobs生成聚类所需要的样本数据：
#样本数据量为300，类簇数量为4，每一个簇内样本标准差为0.50,
X,y=make_blobs(n_samples=300,centers=4,cluster_std=0.50,random_state=0) #X：300行2列的数据根据生成的样本数据，开始进行聚类运算：
#将类簇数量遍历1~10，以便于后面找到合适的K值
list1=[]
for i in range(1,11):
kmeans=KMeans(n_clusters=i,init='k-means++',max_iter=300,n_init=10,random_state=0)
#初始化聚类中心的方式为K-means++,最大迭代次数为300，算法运行次数为10次，随机数种子为0
kmeans.fit(X) #训练数据
list1.append(kmeans.inertia_) #将每次循环训练数据时，聚类得到的每一个类簇的误差平方和添加到列表中看看list1的结果：
print('十次结果的误差平方和:',list1)
#运行结果：十次结果的误差平方和: [2746.776260520676, 1121.4338468225149, 477.68455404063826, 147.2263862575243, 131.1318469883225, 119.16725404063813, 106.51193704849615, 96.12264557325749, 86.52582034564936, 78.70960563748244]为了图形的可视化出现的有关标签以中文以及负号显示，需要设法使得pyplot支持中文和负号：
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False下面开始绘制误差随着K值（1~10）变化的图像：
plt.ylim(0,max(list1)) #设置y轴的范围
plt.xlim(0,11) #设置x轴的范围
plt.plot(range(1,11),list1,c='r')
plt.title('误差随着K的变化曲线')
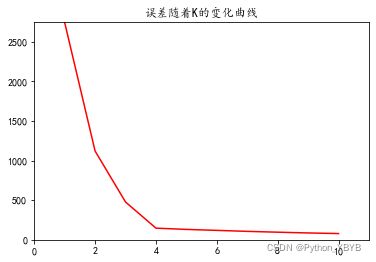
plt.show()图像显示结果如下：
从图中可以看出，K取4的时上述曲线出现拐点同时曲线自此以后下降量都很小了。因此可以考虑以K=4进行聚类：
#以K=4进行聚类：
new_kmeans=KMeans(n_clusters=4,init='k-means++',max_iter=300,random_state=0)
result_y=new_kmeans.fit_predict(X) #对特征数据的聚类结果储存在result_y中
print(result_y) #打印测试
#结果：
[0 2 1 2 0 0 3 1 2 2 3 2 1 2 0 1 1 0 3 3 0 0 1 3 3 1 0 1 3 1 2 2 1 2 2 2 2
2 3 0 1 3 1 1 3 3 2 3 2 0 3 0 2 0 0 3 2 3 2 0 2 1 2 3 3 3 2 0 2 3 1 3 2 3
3 2 3 1 0 2 0 1 0 0 2 1 0 1 2 2 1 0 2 3 3 1 0 0 1 3 2 0 2 0 1 0 0 1 2 1 3
3 0 2 0 1 2 0 0 1 3 0 3 0 0 0 0 3 0 3 2 3 3 0 2 3 3 2 1 2 2 3 1 3 1 3 2 1
2 2 2 1 2 1 0 3 2 3 0 1 2 1 1 0 1 3 3 1 0 1 1 2 0 1 3 2 0 0 1 3 0 1 3 3 1
1 1 1 0 2 1 3 1 1 3 3 3 1 3 2 1 3 0 3 1 2 3 2 1 2 1 3 1 1 2 3 3 0 0 1 2 0
0 3 0 3 1 2 2 1 1 2 1 0 3 1 0 3 2 3 0 1 0 2 2 2 2 3 3 2 1 3 0 1 3 3 3 0 0
2 1 1 3 0 2 3 1 2 1 0 0 3 3 1 0 0 0 1 2 2 0 0 1 0 0 0 2 3 2 1 0 0 2 2 2 0
0 1 2 3]聚类中心：
denters=new_kmeans.cluster_centers_ #聚类中心
print('聚类中心:',denters) #打印测试
#运行结果：
聚类中心:
[[ 1.99469693 0.8727049 ]
[ 0.95415778 4.39985544]
[-1.35241261 7.76731726]
[-1.57480456 2.84532424]]
绘制K=4聚类的图像：
#绘制图形：
fig=plt.figure(figsize=(90,8))
ax1=plt.subplot(131)
ax1.scatter(X[:,0],X[:,1])
ax1.scatter(denters[:,0],denters[:,1],c='r',s=100)
plt.title('K=4的聚类结果')
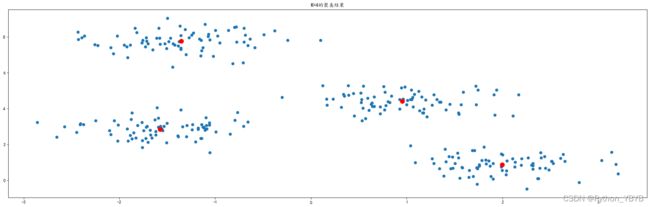
plt.show()运行结果如下图所示：
从图像中，可以看出，K=4时聚合效果较好。
当然，在选择K时，不局限于上述方法。还可以用sklearn模块的metrics中的函数adjusted_rand_score计算ARI找到合适的K进行聚类。不过需要注意的是该方法只适用于数据集含有正确分类标签的情形。当数据集不含分类标签时候，除了上述方法以外，还可以用轮廓系数与K的变化关系情况开选择合适的K值，当轮廓系数最大时，对应的就是最合适的K值。轮廓系数可以通过sklearn库的metrics中的silhouette_score函数进行计算。上述提到的sklearn.metrics中的两个函数可查阅有关资料了解参数声明，此处不再展开说明。
初学Python两个月，对python进行数据分析和机器学习等等方面比较感兴趣，借此机会想和大家一起分享所得和交流有关方面，文中肯定有许多不足之处，望各位大佬多多指教。
本文写作过程中主要参考了以下资料：
1.《Python 数学实验与建模》——司守奎、孙玺菁
2.《Python数据分析从入门代实践》——高春艳、刘志铭
3.《从0开始机器学习的数学原理和算法实践》——大威
4.《Scikit-learn机器学习详解》——潘风文、潘启儒