在tensorflow中使用batch normalization及其原理
在tensorflow中使用batch normalization及其原理
-
- 1.归一化,标准化,正则化
- 2.batch normalization的原理
-
- 2.1归一化
- 2.2平移和缩放
- 3.batch normalization代码
-
- 3.1 tf.nn.moments
- 3.2 tf.train.ExponentialMovingAverage
- 3.3 tf.control_dependencies
- 3.4 tf.identity
- 3.5 tf.cond
对于batch normalization的原理以及相关的名词术语(归一化、标准化)没有弄清楚,最近看到了一篇关于在tensorflow中如何使用batch normalization的文章,以及相关博客,有了一些理解,特此记录。
先了解一下相关的术语以及区别。
1.归一化,标准化,正则化
(1)归一化 Normalization:归一化一般是将数据映射到指定的范围,常见的映射范围有 [0, 1] 和 [-1, 1] ,最常见的归一化方法就是 Min-Max 归一化: x n e w = x − x m i n x m a x − x m i n x_{new}=\frac{x-x_{min}}{x_{max}-x_{min}} xnew=xmax−xminx−xmin
(2)标准化 Normalization:可以看到归一化和标准化的英文单词是相同的,需要根据其用途(或公式)的不同去理解(或翻译),很多人都会把归一化和标准化搞混,所以这也是中文翻译的一个缺陷。最常见的标准化方法就是 Z-Score 标准化: x n e w = x − μ σ x_{new}=\frac{x-\mu}{\sigma} xnew=σx−μ (其中 μ \mu μ是均值, σ \sigma σ是标准差)
(3)特征缩放和均值归一化:在吴恩达老师的机器学习视频介绍了特征缩放和均值归一化,特征缩放一般是通过除以某个数把特征的取值缩放到-1到+1的范围内,而均值归一化的处理方式为 x n e w = x − μ x m a x − x m i n x_{new}=\frac{x-\mu}{x_{max}-x_{min}} xnew=xmax−xminx−μ。
接着介绍一下batch normalization的原理。
2.batch normalization的原理
batch normalization是基于mini-batch梯度下降的,设我们的batch大小为m,输入为x,其算法步骤为:
1.求均值: μ = 1 m ∑ i = 1 m x i \mu=\frac{1}{m}\sum_{i=1}^{m}x_i μ=m1∑i=1mxi
2.求方差: σ 2 = 1 m ∑ i = 1 m ( x i − μ ) 2 \sigma ^2=\frac{1}{m}\sum_{i=1}^{m}(x_i-\mu)^2 σ2=m1∑i=1m(xi−μ)2
3.归一化: x ^ i = x i − μ σ 2 + ξ \hat{x}_i=\frac{x_i-\mu}{\sqrt{\sigma ^2+\xi}} x^i=σ2+ξxi−μ( ξ \xi ξ是为了防止方差 σ 2 \sigma ^2 σ2等于0导致出现分母等于0的情况)
4.平移和缩放: y i = γ x ^ i + β y_i=\gamma \hat{x}_i+\beta yi=γx^i+β( γ \gamma γ和 β \beta β分别称为缩放参数和平移参数)
要理解其原理主要在于上面的第三步和第四步,首先我们来看一下第三步操作的原因以及其作用。
2.1归一化
第三步归一化操作的作用是什么?
Internal Covariate Shift问题:在深层网络的训练过程中,由于参数的不断更新就会引起隐藏层的输入分布不断变化,从而导致上层网络需要不停调整来适应输入数据分布的变化,导致网络学习速度的降低;并且还会使网络的训练过程容易陷入梯度饱和区,减缓网络收敛速度。
如何理解陷入梯度饱和区呢? 一般在训练过程中,随着网络的加深,对于隐藏层来说其输入的整体分布逐渐往非线性激活函数的取值区间的上下限两端靠近(对于Sigmoid函数来说,意味着激活输入值Z=WX+b是大的正值或小的负值),这导致了反向传播时低层神经网络的梯度消失。可以通过具体例子来理解,例如对于非线性函数sigmoid: g ( z ) = 1 1 + e − z g(z)=\frac{1}{1+e^{-z}} g(z)=1+e−z1,及其导数: g ′ ( z ) = 1 1 + e − z ( 1 − 1 1 + e − z ) = g ( z ) ( 1 − g ( z ) ) g'(z)=\frac{1}{1+e^{-z}}(1-\frac{1}{1+e^{-z}})=g(z)(1-g(z)) g′(z)=1+e−z1(1−1+e−z1)=g(z)(1−g(z)),图形如下:
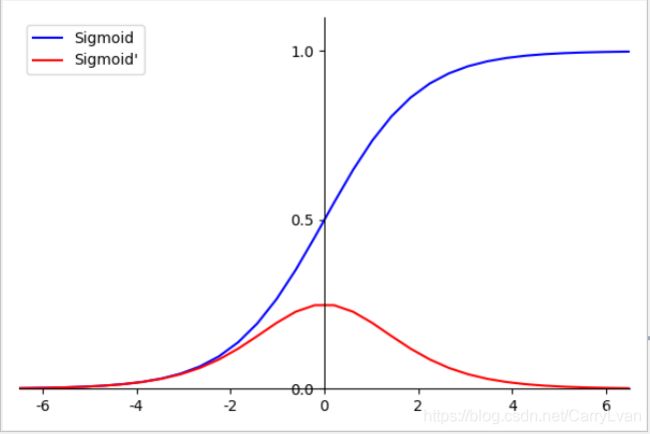
我们再来看一下标准正态分布的含义:意味着在一个标准差范围内,也就是说64%的概率x其值落在[-1,1]的范围内,在两个标准差范围内,也就是说95%的概率x其值落在了[-2,2]的范围内。
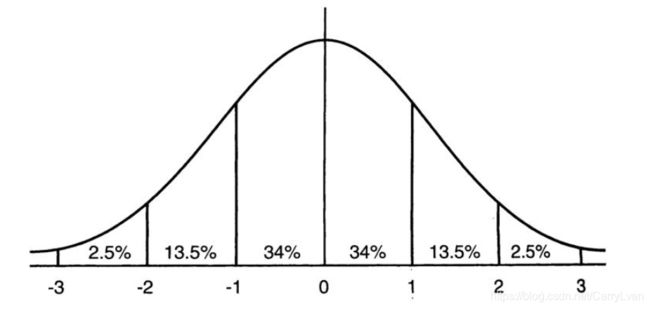
现在假设没有经过BN调整前z的原先正态分布均值是-6,方差是1,那么意味着95%的值落在了[-8,-4]之间,那么对应的Sigmoid(z)函数的值明显接近于0,其导数值也接近于0(上图中的红色曲线),这就是是梯度饱和区;
而为了解决这个问题,BN对输入值z进行归一化后均值是0,方差是1,也就意味着95%的z值落在了[-2,2]区间内,很明显这一段是sigmoid(z)函数接近于线性变换的区域,意味着z的小变化会导致非线性函数值较大的变化,也即是梯度变化较大,对应导数函数图中明显大于0的区域,就是梯度非饱和区。
2.2平移和缩放
为什么要进行平移和缩放这第四步操作?
通过2.1我们知道归一化将输入值的分布调整为均值为0,方差为1的标准正态分布,使得大部分激活函数的值落入到非线性激活函数的线性区域,虽然远离了梯度饱和区,达到了加速学习的速度,但也引来了新的问题。我们知道多层线性网络跟一层线性网络是等价的,并且通过归一化让每一层网络的输入数据分布都变得稳定,导致了数据表达能力的缺失,使得底层网络学习到的参数信息丢失。因此为了保证非线性的获得来保留输入数据的表达能力,对归一化后的值又进行了平移和缩放的操作。

上图是几个正态分布的曲线,绿色的线是标准正态分布,而紫色的线就可以看做使我们对归一化后的值进行平移和缩放后的分布。可以这么理解:每个神经元增加了两个参数 γ \gamma γ(缩放)和 β \beta β(平移)参数,这两个参数是通过训练学习到的,意思是通过 γ \gamma γ(缩放)和 β \beta β(平移)把这个值从标准正态分布左移或者右移一点并长胖一点或者变瘦一点,每个实例挪动的程度不一样,这样等价于非线性函数的值从正中心周围的线性区往非线性区动了动。核心思想应该是想找到一个线性和非线性的较好平衡点,既能享受非线性的较强表达能力的好处,又避免太靠非线性区两头使得网络收敛速度太慢。(来自【深度学习】深入理解Batch Normalization批标准化)
3.batch normalization代码
首先看到代码(来自基础 | batchnorm原理及代码详解)
def batch_norm_layer(x, train_phase, scope_bn):
with tf.variable_scope(scope_bn):
# 新建两个变量,平移、缩放因子
beta = tf.Variable(tf.constant(0.0, shape=[x.shape[-1]]), name='beta', trainable=True)
gamma = tf.Variable(tf.constant(1.0, shape=[x.shape[-1]]), name='gamma', trainable=True)
# 计算此次批量的均值和方差
axises = np.arange(len(x.shape) - 1)
batch_mean, batch_var = tf.nn.moments(x, axises, name='moments')
# 滑动平均做衰减
ema = tf.train.ExponentialMovingAverage(decay=0.5)
def mean_var_with_update():
ema_apply_op = ema.apply([batch_mean, batch_var])
with tf.control_dependencies([ema_apply_op]):
return tf.identity(batch_mean), tf.identity(batch_var)
# train_phase 训练还是测试的flag
# 训练阶段计算runing_mean和runing_var,使用mean_var_with_update()函数
# 测试的时候直接把之前计算的拿去用 ema.average(batch_mean)
mean, var = tf.cond(train_phase, mean_var_with_update,
lambda: (ema.average(batch_mean), ema.average(batch_var)))
normed = tf.nn.batch_normalization(x, mean, var, beta, gamma, 1e-3)
return normed
第一次看这段代码的时候因为对tensorflow中很多函数并不是很了解,所以很多地方都没看到,不过查看了相关文章,略有所了解。
然后现在我们介绍一下上面代码中出现的一些比较陌生的函数。
3.1 tf.nn.moments
上面代码中首先就是tf.nn.moments这个函数,它的作用就是计算均值和方差。
不懂得可以看我上一篇博客:tf.nn.moments( )函数中参数的理解
3.2 tf.train.ExponentialMovingAverage
(1)tf.train.ExponentialMovingAverage这个函数用于更新参数,就是采用滑动平均(也叫指数加权平均)的方法更新参数。
我们先看到函数的定义:
class ExponentialMovingAverage(object):
def __init__(self, decay, num_updates=None, zero_debias=False,
name="ExponentialMovingAverage"):
self._decay = decay
self._num_updates = num_updates
self._zero_debias = zero_debias
self._name = name
self._averages = {}
它其实是ExponentialMovingAverage类的一个初始化函数,我们调用tf.train.ExponentialMovingAverage(decay, num_updates)实际上是创建的一个ExponentialMovingAverage类的对象。
参数:
decay是衰减率,用于控制模型的更新速度。
s h a d o w _ v a r i a b l e = d e c a y ∗ s h a d o w _ v a r i a b l e + ( 1 − d e c a y ) ∗ v a r i a b l e shadow\_variable = decay * shadow\_variable + (1-decay) * variable shadow_variable=decay∗shadow_variable+(1−decay)∗variable
( s h a d o w _ v a r i a b l e shadow\_variable shadow_variable就是我们通过apply添加变量的影子变量, v a r i a b l e variable variable则是我们添加的训练变量。)
每次更新完以后,影子变量的值更新,varible的值就是你设定的值。如果在下一次运行这个函数的时候你不在指定新的值,那就不变,影子变量更新。如果指定,那就variable改变,影子变量也改变。
num_updates是用来动态设置decay衰减率的。
d e c a y = m i n ( d e c a y , 1.0 + n u m _ u p d a t e s 10.0 + n u m _ u p d a t e s ) decay=min(decay, \frac{1.0 + num\_updates}{10.0 + num\_updates}) decay=min(decay,10.0+num_updates1.0+num_updates)
(2)ExponentialMovingAverage类中还提供了apply函数,简单来说就是添加我们的训练变量,用于上面影子变量的更新。在每次训练之后调用此操作,更新移动平均值
def apply(self, var_list=None):
(3)ExponentialMovingAverage类还提供了average和average_name函数,分别来取出我们的apply存入的变量和变量名。
def average(self, var):
return self._averages.get(var, None)
def average_name(self, var):
因为在ExponentialMovingAverage类中,我们通过apply函数添加的训练变量都存在了_average属性中,这是一个字典类型,apply传入的参数就是我们要找的变量(字典中的键),然后通过get函数取出来。
先看到一个例子:
import tensorflow as tf
w = tf.Variable(1.0)
x = tf.Variable(3.0)
ema = tf.train.ExponentialMovingAverage(0.9)
update = tf.assign_add(w, 1.0)
update2 = tf.assign_add(x, 1.0)
with tf.control_dependencies([update, update2]):
#返回一个op,这个op用来更新moving_average,i.e. shadow value
ema_op = ema.apply([w,x])
# 以 w 当作 key, 获取 shadow value 的值
ema_val = ema.average(w)#参数不能是list
ema_val2 = ema.average(x)
with tf.Session() as sess:
tf.global_variables_initializer().run()
for i in range(3):
sess.run(ema_op)
print("w: ",sess.run(ema.average(w)))
print("x: ", sess.run(ema_val2))
print(w)
print(x)
print(ema._averages)
输出:
w: 1.1
x: 3.1
w: 1.2900001
x: 3.29
w: 1.5610001
x: 3.561
<tf.Variable 'Variable:0' shape=() dtype=float32_ref>
<tf.Variable 'Variable_1:0' shape=() dtype=float32_ref>
{<tf.Variable 'Variable:0' shape=() dtype=float32_ref>: <tf.Variable 'Variable/ExponentialMovingAverage:0' shape=() dtype=float32_ref>, <tf.Variable 'Variable_1:0' shape=() dtype=float32_ref>: <tf.Variable 'Variable_1/ExponentialMovingAverage:0' shape=() dtype=float32_ref>}
当我们第一调用apply函数的时候,如果w是Variable,那么就会用w的值来初始化 s h a d o w _ v a r i a b l e shadow\_variable shadow_variable,而当w是tensor时, s h a d o w _ v a r i a b l e shadow\_variable shadow_variable会被初始化为0.0。在这里w是Variable,所以在第一次循环的时候,我们的w的更新计算是:0.9*1+(1-0.9)*2=1.1。
并且我们通过打印w,x,ema._averages也能看到字典中存放的变量,以及average的原理。
注意,上面我们更新只能通过更新w和x,然后重新sess.run(ema.apply返回的op),如果我们多次调用ema.apply,则会报错已经计算过。在这里我们是通过加入下面将要讲的上下文控制器tf.control_dependencies来实现每次sess.run(ema_op)的时候都会先更新我们的变量。
3.3 tf.control_dependencies
tf.control_dependencies(control_inputs)是tensorflow中的一个flow顺序控制机制,返回一个上下文管理器(通常与with一起使用)。
通过下面这个例子看一下:
with tf.control_dependencies([a, b, c]):
d = ...
e = ...
session在运行d、e之前会先运行a、b、c,并且在with tf.control_dependencies之内的代码块受到顺序控制机制的影响。
注意只有d、e是op(节点操作)的时候才会在d、e之前会先运行a、b、c。
举个例子说明一下是怎么执行的:
例子1:
import tensorflow as tf
w = tf.Variable(1.0)
x = tf.Variable(2.0)
update = tf.assign_add(w, 1.0)
with tf.control_dependencies([update]):
op = w*x
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for i in range(3):
print(sess.run(op))
输出结果
4.0
6.0
8.0
当我们循环执行sess.run(op)的时候,由于op依赖于于上下文管理器,所以在每次执行之前会先执行tf.control_dependencies([updates])中的updates。
例子2:
import tensorflow as tf
w = tf.Variable(1.0)
update = tf.assign_add(w, 1.0)
with tf.control_dependencies([update]):
a = w
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for i in range(3):
print(sess.run(a))
输出结果:
1.0
1.0
1.0
按照我们前面的猜想应该输出2,3,4。但是结果却是1 1 1,这是因为a并不是一个op(节点操作)。
上面batch normalization代码中就是通过tf.control_dependencies添加依赖,在每次执行更新的时候都会先apply添加当前batch的均值和方差,然后通过滑动平均的方式更新变量。
3.4 tf.identity
在上面的代码中如果直接return batch_mean, batch_var,会出问题,因为batch_mean,batch_var并不是一个op,所以这个上下文管理器就失效了,而tf.identity是返回一个一模一样新的tensor的op,这会增加一个新节点到gragh中,这时control_dependencies就会生效。
通过上面的例子2来说明一下:
import tensorflow as tf
w = tf.Variable(1.0)
update = tf.assign_add(w, 1.0)
with tf.control_dependencies([update]):
op = tf.identity(w)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for i in range(3):
print(sess.run(op))
输出结果
2.0
3.0
4.0
上面的例子2中是输出1.0 1.0 1.0,这里却不是,因为tf.identity返回了一个一模一样新的tensor的op,这个时候,上下文管理器的依赖就会起作用了,每次循环前都会更新w的值。
3.5 tf.cond
直接通过一个例子来说明一下
z = tf.multiply(a, b)
result = tf.cond(x < y, lambda: tf.add(x, z), lambda: tf.square(y))
如果x 现在看到上面我们的代码最后一句: 这是tensorflow中为我们提供的batch normalization的函数,他实现的功能就是上面原理中的第3步和第4步,参数mean和var分别是我们的均值和方差,beta和 gamma分别是平移参数和缩放参数,1e-3就是为了防止分母等于0这种情况的 ξ \xi ξ。 参考文章:基础 | batchnorm原理及代码详解
tf.nn.batch_normalization(x, mean, var, beta, gamma, 1e-3)
所以要实现完整的batch norm我们还需要自己实现计算均值和方差的代码,这就是上面这段代码的由来。
【深度学习】深入理解Batch Normalization批标准化
Batch Normalization原理与实战
tf.train.ExponentialMovingAverage的用法
tf.control_dependencies()
tf.identity的意义以及用例
tf.cond()的用法