人工智能-作业4：CNN - 卷积

一、简单描述卷积、卷积核、多通道、特征图、特征选择概念。

1. 卷积

卷积是分析数学中一种重要的运算。
简单定义：设$f(x)$, $g(x)$是R1上的的两个可积函数，作积分：
$${\int }_{-\infty }^{+\infty }f(x)g(x)dx$$
可以证明，关于几乎所有的实数$x$，上述积分是存在的。这样，随着$x$的不同取值，这个积分就定义了一个新函数，称为函数与的卷积，记为$h(x)=(f.g)(x)$。
图片：

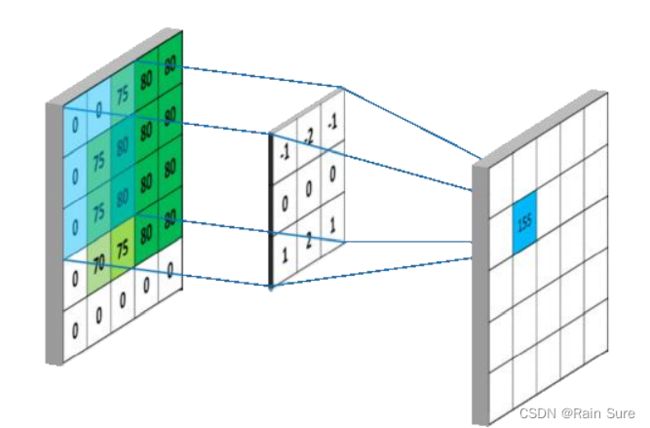
2. 卷积核(Kernel)

在图像卷积计算中，需要定义一个卷积核(Kernel)。卷积核是一个二维矩阵，矩阵中数值为对图像中与卷积核同样大小的子块像素点进行卷积计算时所采用的权重。

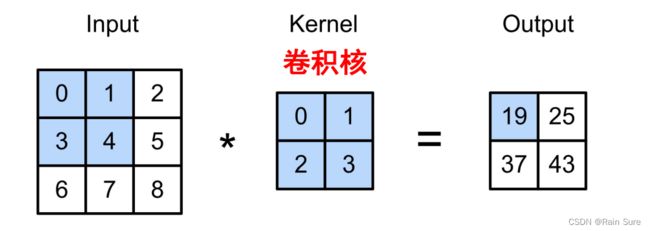
3. 多通道

多通道图像是指多个摄像机拍摄的同一个场景的图像或者一个摄像机在不同时刻拍摄的同一场景的图像。在表示图像时，使用多个通道对图像进行编码。多通道图像常用于人工智能领域。

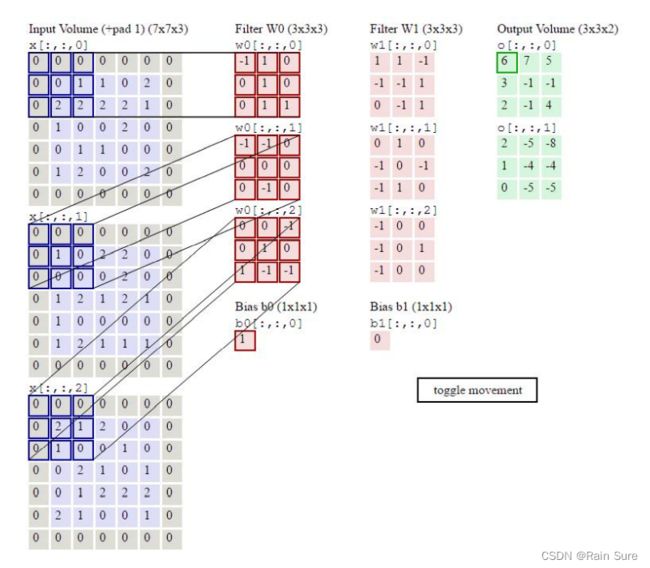
4. 特征图(feature map)

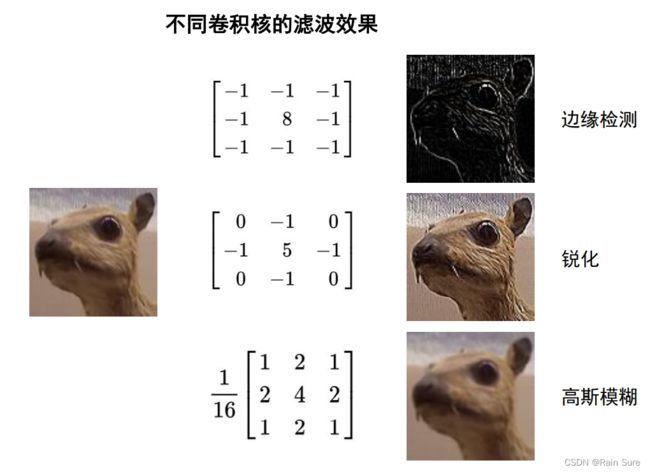
如下图所示，图像与卷积核加权累加得到卷积(滤波)后的特征图。卷积滤波结果在卷积神经网络中被称为特征图。

5. 特征选择

人的视觉神经细胞对不同的视觉模式具有特征选择性，不同视觉神经细胞对边界、运动和颜色等不同信息具有强弱不同的选择性。
不同的卷积核可用来被刻画不同的选择性。

二、探究不同卷积核的作用，研究背后的原理。

不同卷积核具有不同的滤波效果：

1.边缘检测

边缘检测的卷积核：

作用：使用边缘检测卷积核可以有效识别图像的边缘，边缘检测的目的是标识数字图像中亮度变化明显的点。图像属性中的显著变化通常反映了属性的重要事件和变化。
边缘检测的目的就是找到图像中亮度变化剧烈的像素点构成的集合，表现出来往往是轮廓。

2. 锐化

图像锐化的卷积核：

作用：
图像锐化也称边缘增强。锐化技术用于加强图像中的边界和细节信息。由于边界和细节信息对应频域中的高频部分，所以在频域中通常对图像进行高通滤波，在空间域则进行微分处理。

结果：

3. 模糊

图像模糊的卷积核

三、编程实现：

1. 经典卷积核，实现灰度图的边缘检测、锐化、模糊。

边缘检测

代码：

import numpy as np
import torch
from torch import nn
from torch.autograd import Variable
import torch.nn.functional as F
from PIL import Image
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号 #有中文出现的情况，需要u'内容
# https://blog.csdn.net/weixin_40123108/article/details/83510592
file_path = 'test.jpg'
im = Image.open(file_path).convert('L')  # 读入一张灰度图的图片
im = np.array(im, dtype='float32')  # 将其转换为一个矩阵
print(im.shape[0], im.shape[1])
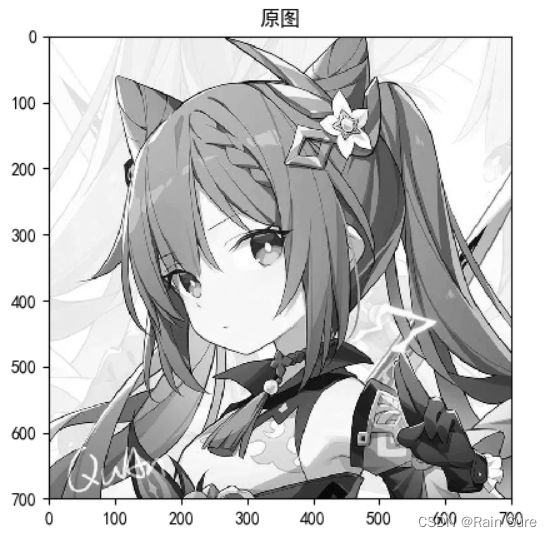
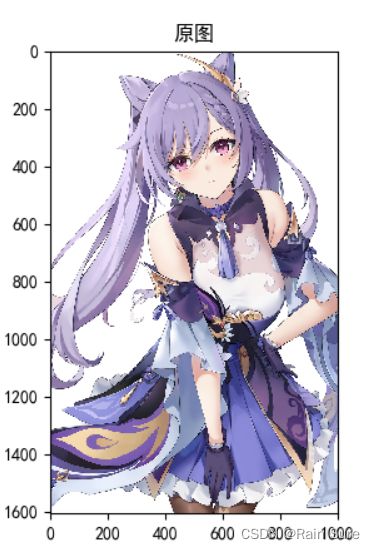
plt.imshow(im.astype('uint8'), cmap='gray')  # 可视化图片
plt.title('原图')
plt.show()

im = torch.from_numpy(im.reshape((1, 1, im.shape[0], im.shape[1])))
conv1 = nn.Conv2d(1, 1, 3, bias=False)  # 定义卷积

sobel_kernel = np.array([[-1, -1, -1],
                         [-1, 8, -1],
                         [-1, -1, -1]], dtype='float32')  # 定义轮廓检测算子
sobel_kernel = sobel_kernel.reshape((1, 1, 3, 3))  # 适配卷积的输入输出
conv1.weight.data = torch.from_numpy(sobel_kernel)  # 给卷积的 kernel 赋值

edge1 = conv1(Variable(im))  # 作用在图片上

x = edge1.data.squeeze().numpy()
print(x.shape)  # 输出大小

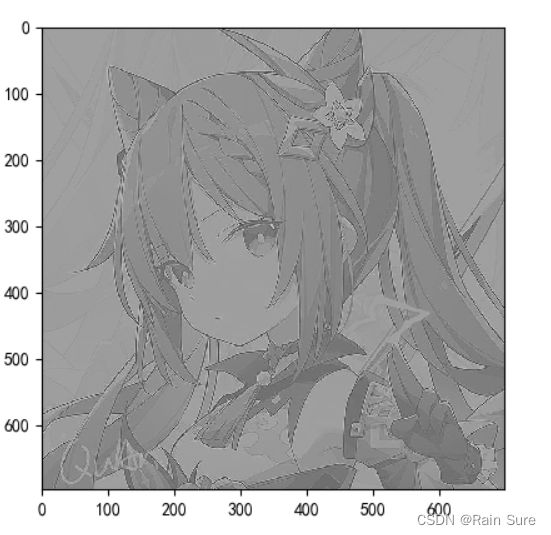
plt.imshow(x, cmap='gray')
plt.show()

运行结果展示
原图：

进行边缘检测：

锐化

改变卷积核：

锐化处理：

模糊

改变卷积核为模糊卷积核：

运行结果：

2.调整经典卷积核参数，测试并总结。

边缘检测

尝试改变中心参数：
降低中心参数，会发现边缘检测会变差很多。

增大中心参数，边缘检测效果同样会变差很多

锐化

增大周围参数，使周围权重升高。

可以由结果看出，锐化效果变弱了很多。

降低周围参数，使得周围元素权重降低：

锐化效果变强了很多。。。图片也阴间了很多。

模糊

改变模糊卷积核参数。

改变了一下参数，让参数更接近了，但确实没出来什么变化。。。

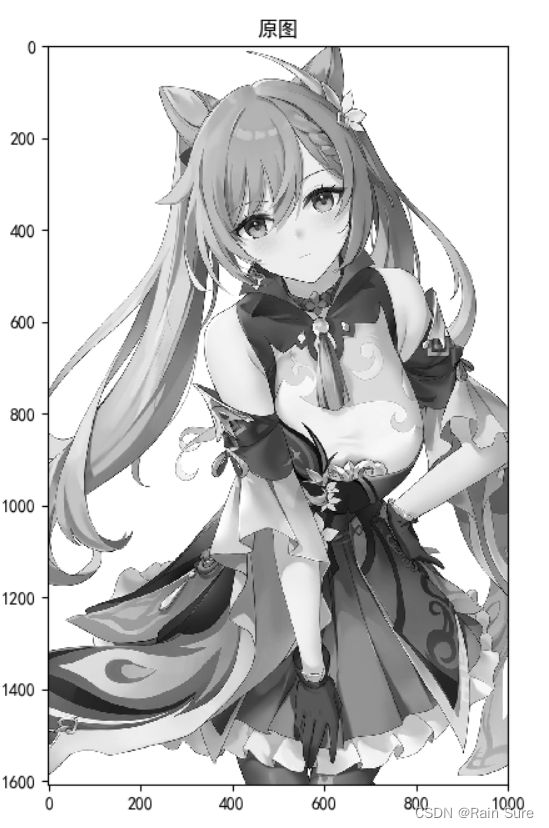
3. 使用不同尺寸图片，测试并总结

换了一张分辨率不同的图片，高度变高了，宽度变小了。

4. 探索更多类型卷积核。

1. bottom sobel
   卷积核：
   

2. emboss


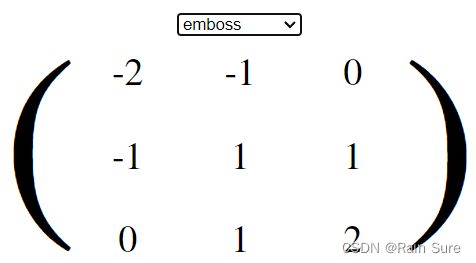
3. left sobel


4. right sobel


5. top sobel

5. 尝试彩色图片边缘检测

将代码读入灰度图部分，改为读入彩色图

就挺神奇的。。。

四、总结

感觉还是挺有意思的，光靠上课听是不够的，下课玩一玩就忘了很多，还要自己看书复习复习，还有多写写代码加深理解！

五、参考文献

卷积神经网络超详细介绍
卷积神经网络（CNN）中的卷积核 概念 原理
【2021-2022 春学期】人工智能-作业4：CNN - 卷积