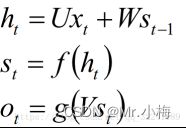从RNN到Attention到Transformer系列-RNN介绍、手动计算验证
深度学习知识点总结
专栏链接:
深度学习知识点总结_Mr.小梅的博客-CSDN博客本专栏主要总结深度学习中的知识点，从各大数据集比赛开始，介绍历年冠军算法；同时总结深度学习中重要的知识点，包括损失函数、优化器、各种经典算法、各种算法的优化策略Bag of Freebies (BoF)等。
本章介绍从RNN到Attention到Transformer系列-RNN
目录
3.1 RNN
3.1.1 RNN介绍
3.1.2 PyTorch中RNN的计算
3.1.3 RNN手动计算验证
3.1.4 RNN存在的问题
3.1 RNN
3.1.1 RNN介绍
循环神经网络（Recurrent Neural Network, RNN）是一类以序列（sequence）数据为输入，在序列的演进方向进行递归（recursion）且所有节点（循环单元）按链式连接的递归神经网络（recursive neural network）。
对循环神经网络的研究始于二十世纪80-90年代，并在二十一世纪初发展为深度学习（deep learning）算法之一，其中双向循环神经网络（Bidirectional RNN, Bi-RNN）和长短期记忆网络（Long Short-Term Memory networks，LSTM）是常见的循环神经网络。
循环神经网络具有记忆性、参数共享并且图灵完备（Turing completeness），因此在对序列的非线性特征进行学习时具有一定优势。
循环神经网络在自然语言处理（Natural Language Processing, NLP），例如语音识别、语言建模、机器翻译等领域有应用，也被用于各类时间序列预报。引入了卷积神经网络（Convolutional Neural Network,CNN）构筑的循环神经网络可以处理包含序列输入的计算机视觉问题。
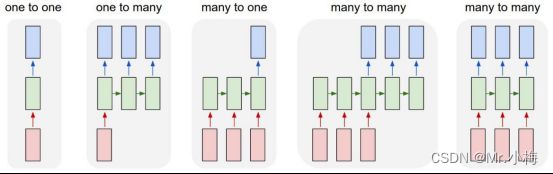
每个矩形都是一个向量，箭头表示函数（例如矩阵乘法）。输入向量为红色，输出向量为蓝色，绿色向量保持RNN的状态（稍后将详细介绍）。
从左到右：
- 没有RNN的普通处理模式，从固定大小的输入到固定大小的输出（例如图像分类）。
- 序列输出（例如，图像字幕拍摄图像并输出单词句子）。
- 序列输入（例如，情绪分析，其中给定的句子被归类为表达积极或消极的情绪）。
- 序列输入和序列输出（例如机器翻译：RNN用英语读取句子，然后用法语输出句子）。
- 同步序列输入和输出（例如，我们希望标记视频的每一帧的视频分类）。请注意，在每种情况下，长度序列上都没有预先指定的约束，因为循环变换（绿色）是固定的，可以根据需要多次应用。
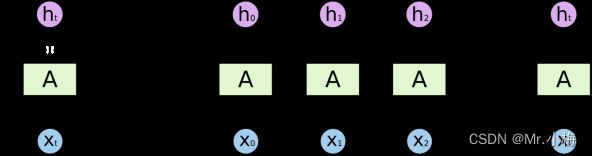
RNN的基本形状：
展开后：
注意:
- 这里的W,U,V在每个时刻都是相等的(权重共享).
- 隐藏状态可以理解为: S=f(现有的输入+过去记忆总结)
用代码实现RNN：
import numpy as np
class RNN:
# ...
def step(self, x):
# update the hidden state
self.h = np.tanh(np.dot(self.W_hh, self.h) + np.dot(self.W_xh, x))
# compute the output vector
y = np.dot(self.W_hy, self.h)
return y一个 RNN 接收输入向量，第二个 RNN 接收第一个 RNN 的输出作为其输入。
展开后如下：
3.1.2 PyTorch中RNN的计算
Pytorch中RNN的定义：
torch.nn.RNN(*args, **kwargs)
初始化RNN所需参数：
Parameters
- input_size – 输入x的特征数，例如每句话中每个单词的特征数
- hidden_size – 隐藏层特征数，一般就是RNN输出的特征数
- num_layers – 隐藏层层数，默认为1
- nonlinearity – 非线性函数 'tanh' or 'relu'. Default: 'tanh'
- bias – 是否使用bias( b_ih and b_hh). Default: True
- batch_first – 如果设置为True的话，输入batchsize放到前面，Default: False
- dropout – Default: 0
- bidirectional – 设置为True变成双向RNN Default: False
使用RNN时的输入参数：
Inputs: input, h_0
- input: batch_first=False时尺寸为(L,N,
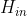)，batch_first=True时尺寸为(N, L, 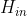) - h_0：输入尺寸为(D∗num_layers,N,
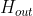) ，不输入时默认为0。
RNN的输出：
Outputs: output, h_n
- output：当batch_first=False时输出尺寸为(L, N, D * H_{out})；当batch_first=True时输出尺寸为(N, L, D * H_{out})
- h_n：(D∗num_layers,N,Hout) 各个隐藏状态参数
以上各个字母的解释：
- N=batch size
- L=sequence length输入序列的长度
- D=2 if bidirectional=True otherwise 1
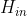- =input_size输入特征长度
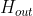- =hidden_size输出特征长度
RNN中可训练的参数
- RNN.weight_ih_l[k] – 第k层输入层-隐藏层权重k = 0时shape=(hidden_size, input_size) ，k>0时shape=(hidden_size,num_directions * hidden_size)
-
RNN.weight_hh_l[k] – 第k层隐藏-隐藏层权重，shape=(hidden_size, hidden_size)
-
RNN.bias_ih_l[k] – 第k层输入层-隐藏层bias，shape=(hidden_size)
-
RNN.bias_hh_l[k] – 第k层隐藏-隐藏层bias，shape=(hidden_size)
所有可训练参数初始化范围(-sqrt(k),sqrt(k)),k=1/(hidden_size)
3.1.3 RNN手动计算验证
PyTorch的计算结果
import torch
import torch.nn as nn
torch.random.manual_seed(654)
rnn = nn.RNN(input_size=1, hidden_size=3,
num_layers=1, bidirectional=False,
nonlinearity='relu', bias=False)
print(rnn.weight_ih_l0)
'''''shape(1,3)
[[0.4389],
[0.3772],
[-0.3647]]
'''
print(rnn.weight_hh_l0)
'''shape(3,3)
[[0.3091,-0.0224,0.4010],
[-0.1867,-0.5099,0.4860],
[0.4007,0.2936,0.1126]]
'''
h0 = torch.ones((1, 2, 3))
'''
h10=[[[1.,1.,1.],
[1.,1.,1.]]]
'''
x = torch.randn((5, 2, 1)) # shape(sequence length,batchsize,input_size)
print(x)
'''shape(5,2,1)
[[[0.1416],
[0.6004]],
[[-1.1653],
[-2.1373]],
[[1.3519],
[-0.7998]],
[[-0.2477],
[0.1398]],
[[0.2404],
[0.3897]]]
'''
output, hidden = rnn(x, h0)
print(output)
print(output.shape)
'''shape=[5,2,3]
[[[0.7498,0.0000,0.7552],
[0.9512,0.0159,0.5879]],
[[0.0232,0.0000,0.8105],
[0.0000,0.0000,1.2314]],
[[0.9255,0.8995,0.0000],
[0.1428,0.2968,0.4304]],
[[0.1572,0.0000,0.7252],
[0.2714,0.0839,0.1419]],
[[0.4449,0.4138,0.0570],
[0.3099,0.1225,0.0073]]]
'''
print(hidden)
print(hidden.shape)
'''shape=[1,2,3]
[[[0.4449,0.4138,0.0570],
[0.3099,0.1225,0.0073]]]
'''手动计算验证
'''
h0 = 1,1,1,... -> shape(1,2,3)
x -> shape(5,2,1) 输入数据，相当于batchsize=2，输入了5个词，每个词的向量维度是1
[[[ 0.1416],
[ 0.6004]],
[[-1.1653],
[-2.1373]],
[[ 1.3519],
[-0.7998]],
[[-0.2477],
[ 0.1398]],
[[ 0.2404],
[ 0.3897]]]
Wih -> shape(1,3) 即rnn.weight_ih_l0输入层到隐藏层之间的参数
[[ 0.4389],
[ 0.3772],
[-0.3647]]
Whh -> shape(3,3)即即rnn.weight_hh_l0隐藏层到隐藏层之间的参数
[[ 0.3091, -0.0224, 0.4010],
[-0.1867, -0.5099, 0.4860],
[ 0.4007, 0.2936, 0.1126]]
初始化的隐藏层参数 shape(1,2,3)
h10 = [[[1., 1., 1.],
[1., 1., 1.]]]
# 首先输入x的第一个词x[0] 计算过程如下
U·Xt=torch.matmul(torch.unsqueeze(x[0],0),rnn.weight_ih_l0.T)
W·S10=torch.matmul(torch.ones((1,2,3)),rnn.weight_hh_l0.T)
得到第一个单词的输出
S11 = ReLU(Wih·x0 + Whh·h10)
= ReLU(
[[[0.1416],
[0.6004]]]
·
[[ 0.4389],
[ 0.3772],
[-0.3647]].T
+
[[[1., 1., 1.],
[1., 1., 1.]]]
·
[[ 0.3091, -0.0224, 0.4010],
[-0.1867, -0.5099, 0.4860],
[ 0.4007, 0.2936, 0.1126]].T
)
= ReLU([[[ 0.7498, -0.1572, 0.7552],
[ 0.9512, 0.0159, 0.5879]]])
=[[[0.7498, 0.0000, 0.7552],
[0.9512, 0.0159, 0.5879]]]
第一个单词的输出作为第二个单词的输出
U·Xt==torch.matmul(torch.unsqueeze(x[1],0),rnn.weight_ih_l0.T)
W·S11=torch.matmul(torch.tensor([[[0.7498, 0.0000, 0.7552],
[0.9512, 0.0159, 0.5879]]]),rnn.weight_hh_l0.T)
得到第二个单词的输出
S12 = ReLU(Wih·x1 + Whh·h12)
= ReLU(
[[[-1.1653],
[-2.1373]]]
·
[[ 0.4389],
[ 0.3772],
[-0.3647]].T
+
[[[0.7498, 0.0000, 0.7552],
[0.9512, 0.0159, 0.5879]]]
·
[[ 0.3091, -0.0224, 0.4010],
[-0.1867, -0.5099, 0.4860],
[ 0.4007, 0.2936, 0.1126]].T
)
= ReLU([[[ 0.0232, -0.2125, 0.8104],
[-0.4085, -0.7062, 1.2314]]])
=[[[0.0232, 0.0000, 0.8104],
[0.0000, 0.0000, 1.2314]]]
....
后续几个词类似，最后得到
out = torch.vstack([S11,S12,S13,S14,S15])
最后的隐藏层输出即为最后一个out,即out[-1]
hn = h15
'''3.1.4 RNN存在的问题
长期依赖的问题
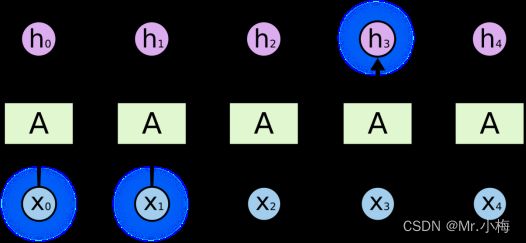
RNN的吸引力之一是它们可能能够将以前的信息与当前任务联系起来的想法，例如使用以前的视频帧可能会告知对当前帧的理解。如果RNN可以做到这一点，它们将非常有用。但是他们能做到吗？这要视情况而定。
有时，我们只需要查看最近的信息即可执行当前任务。例如，考虑一个语言模型，该模型试图根据前一个单词预测下一个单词。如果我们试图预测“the clouds are in the sky”中的最后一个词，我们不需要任何进一步的上下文 - 很明显，下一个词将是sky。在这种情况下，如果相关信息与需要它的地方之间的差距很小，RNN可以学习使用过去的信息。
但在某些情况下，我们需要更多的背景。考虑尝试预测文本中的最后一个词“我在法国长大......我说一口流利的法语。最近的信息表明，下一个词可能是一种语言的名称，但如果我们想缩小哪种语言的范围，我们需要法国的上下文，从更远的地方。相关信息与需要它的点之间的差距完全有可能变得非常大。
不幸的是，随着这种差距的增长，RNN无法学会连接信息。
于是就有了后来的LSTM。