24-梯度下降的向量化和数据标准化

梯度下降的向量化和数据标准化

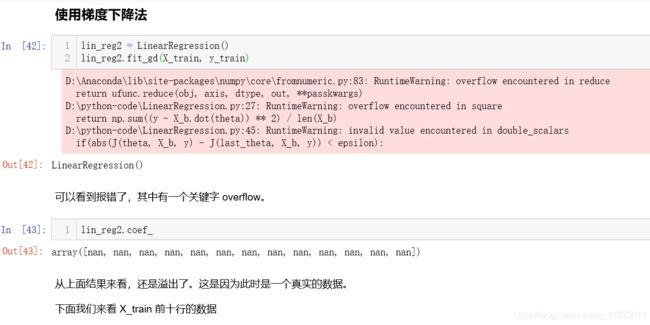
  这篇博客主要介绍应用梯度下降法来进行训练这种线性回归模型应用在真实的数据上。

  那么在这之前，我们还是处理这样的一个问题，如何对我们的梯度下降法过程进行向量化的处理，那么对于向量化的处理，主要集中在我们求梯度的过程：

  我们在上一篇博客中，求解的方式是一项一项的将梯度中对应的元素给求出来，使用了一个 for 循环，对于这个式子，我们能不能进一步进行向量化，将其转换成矩阵的运算呢？再仔细看看式子，里面各项的形式很一致，通常来说是可以的，下面我们来进行一下尝试。

  这里我们首先看到第 0 项，它和其他项不一样，我们让它和其他项进行统一，统一的方式也很简单，就是在第 0 项后面再点乘一个 $X0(i)$，我们让 $X0(i)$ 恒等于 1。

  那么下面我们的任务就是对式子(2)进行向量化处理。回忆一下，在上一篇博客实现的时候，其实那个 for 循环里面已经一定程度的向量化了式子(2) 中每一个元素对应的这个式子：

  我们已经将每个元素对应的式子看成了两个向量对应的点乘这样的形式（使用了 $dot$），两个向量分别是：

这样，我们梯度里面的式子，可以理解成一个矩阵的运算。

对于这个式子：

我们将其展开，得到：

那么我们是不是可以将这个式子看成两个向量相乘：

所以将其推广到整个 $J(\theta )$，可以将其看成：

  这样就将之前求梯度的过程，转换成了两个矩阵相乘，$A$ 矩阵为 1 x $m$ 的矩阵，$B$ 为 $m$ x $(n+1)$ 的矩阵。这样的两个矩阵相乘后为 1 x $(n+1)$ 的矩阵，而原来我们要求的梯度里，也有 $n+1$ 个元素，相应的这两个向量中对应的 $n+1$ 个元素是相等的，一一对应的。

  我们再观察一下矩阵 $B$：

  其实它就是我们之前的 $X_b$，第一列就是 $X_0$，恒等于 1，其他的部分就是我们原来的样本对应的 $X$，是一个 $m$ x $n$ 的矩阵，所以我们就可以将梯度这个式子写成这么简单的一个形式：

  这里为什么要进行一个转置运算（$T$）呢？因为我们之前规定的在学习的过程中所有向量都是用列向量表示，所以这里需要进行一个转置运算，将其转换成一个行向量。

  那么你可能会意识到一个问题，就是按照上述式子求出来的是一个 1 x $(n+1)$ 的行向量，而我们原始的梯度表达式为 $(n+1)$ x 1 的列向量，之前我们有说过，在 $numpy$ 中，对于向量的表示是不区分行向量列向量的，所以我们按照这个式子计算也无妨。但是在这里，为了严谨起见，我们还是将这个式子相应的转换成一个列向量。那么转换的方式也很简单，我们可以将转换的结果整体再进行一下转置，所以我们形成这样一个式子：

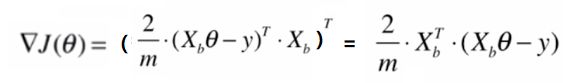
  那么我们只需要修改 $dJ$ 函数即可：

import numpy as np
from metrics import r2_score

class LinearRegression:
    def __init__(self):
        """初始化 Linear Regression"""
        self.coef_ = None           # 系数
        self.interception_ = None   # 截距
        self._theta = None          # θ
    def fit_normal(self, X_train, y_train):
        """根据训练数据集X_train，y_train训练Linear Regression模型"""
        assert X_train.shape[0] == y_train.shape[0], \
            "the size of X_train must be equal to the size of y_train"
        X_b = np.hstack([np.ones((len(X_train), 1)), X_train]) # 在 X_train 前加一列 1
        self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)

        self.interception_ = self._theta[0]     #截距
        self.coef_ = self._theta[1:]            #系数

        return self
    def fit_gd(self, X_train, y_train, eta=0.01, n_iters=1e4):
        """根据训练数据集X_train，y_train，使用梯度下降法训练Linear Regression模型"""
        assert X_train.shape[0] == y_train.shape[0], \
            "the size of X_train, y_train must be equal to the size of y_train"
        def J(theta, X_b, y):
            try:
                return np.sum((y - X_b.dot(theta)) ** 2) / len(X_b)
            except:
                return float('inf')
        def dJ(theta, X_b, y):
            # res = np.empty(len(theta))
            # res[0] = np.sum(X_b.dot(theta) - y)
            # for i in range(1, len(theta)):
            #     res[i] = np.sum((X_b.dot(theta) - y).dot(X_b[:, i]))
            # return res * 2 / len(X_b)
            return X_b.T.dot(X_b.dot(theta) - y) * 2 / len(X_b)
        def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):
            theta = initial_theta
            i_iter = 0
            while i_iter < n_iters:
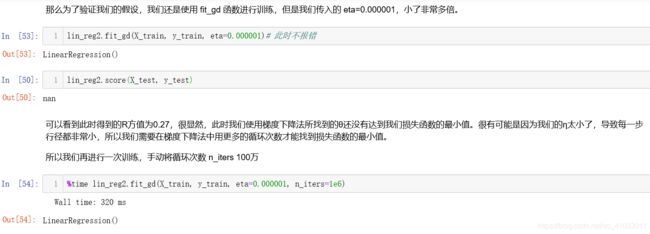
                gradient = dJ(theta, X_b, y)
                last_theta = theta
                theta = theta - eta * gradient

                if(abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
                    break
                i_iter += 1
            return theta
        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        initial_theta = np.zeros(X_b.shape[1])
        self._theta = gradient_descent(X_b, y_train, initial_theta, eta)

        self.interception_ = self._theta[0]
        self.coef_ = self._theta[1:]
        return self
    def predict(self, X_predict):
        """给定待预测数据集X_predict，返回表示X_predict的结果向量"""
        assert self.interception_ is not None and self.coef_ is not None, \
            "must fit before predict!"
        assert X_predict.shape[1] == len(self.coef_), \
            "the feature number of X_predict must be equal to X_train"
        X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
        return X_b.dot(self._theta)
    def score(self, X_test, y_test):
        """根据测试数据集X_test和y_test确定当前模型的准确度"""
        y_predict = self.predict(X_test)
        return r2_score(y_test, y_predict)
    def __repr__(self):
        return "LinearRegression()"

---

测试

下面就开始进行测试：

---

下一篇博客我将介绍随机梯度下降法~~

具体代码见 24 梯度下降法的向量化.ipynb