机器学习之欠拟合与过拟合(一)
机器学习之欠拟合与过拟合(一)
1.欠拟合(underfitting)与过拟合(overfitting)
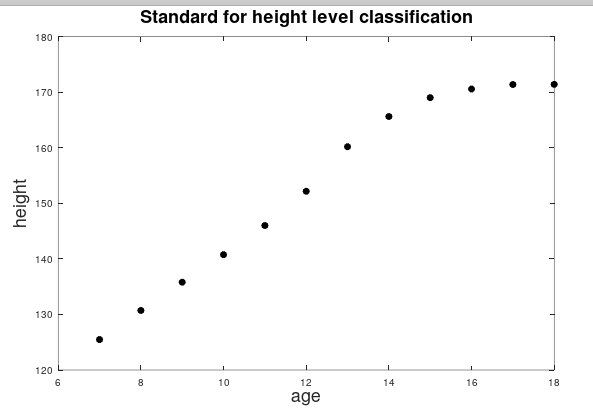
在机器学习中,我们的主要思想是通过对数据集的学习来生成我们的假设模型。在对数据集进行拟合的过程中,我们可能会遇到欠拟合和过拟合的问题。以身高预测的例子为例,这里给出7-18岁男生的身高标准(数据来源:7 岁~18 岁儿童青少年身高发育等级评价),如图1:
将中位数随年龄的变化绘制成散点图,如图2:
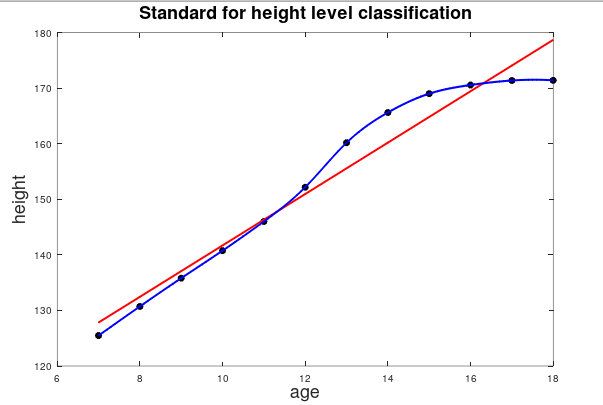
由图2中的散点可知,先开始身高随年龄几乎成一条直线关系,后来增长率逐渐下降。如果我们采用线性函数取拟合,这显然是不合理的(线性函数的增长率不会发生变化)。如果我们用一个多项式函数去拟合,虽然这个多项式可能会很复杂,但是我们总可能找到一个多项式函数使得该函数完美经过图中的散点,如图3:
现在,我们来看一下线性拟合(图3红线):年龄大于18岁以后,按照散点图的趋势,身高应该逐渐趋于稳定,但是线性拟合的结果是身高随年龄增长依旧保持很高的增长率。显然这并不是一种很好的拟合方式,对于这种情况,我们称之为欠拟合,即高偏差(high bias)。
接下来,我们来看一下“完美的多项式拟合”(图3蓝线):蓝线的损失函数为0,在回归问题中,我们求解参数矩阵的方法就是尽可能地让损失函数的值最小化。这是否意味着当损失函数为0时,这时我们的学习模型最好呢?并不是这样子的。在”完美的多项式拟合“当中,我们的假设函数通常情况下会非常复杂,一般会涉及到高次多项式,函数图像会非常扭曲。以五次多项式为例,即便我们的自变量之间的偏差数量级为10,但对应输出结果的偏差会达到 1 0 5 10^5 105数量级。图3的例子可能还不明显,图4很好的说明了“完美拟合”的扭曲情况。对于这种为了最小化损失函数,而将假设函数“过度扭曲”的情况,我们称之为过拟合,即高方差(high variance)。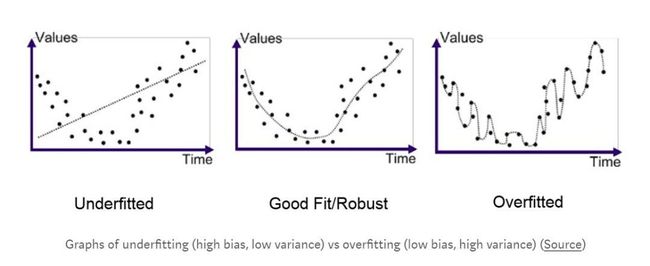
2.偏差(bias)和方差(variance)
2.1偏差和误差的概念
偏差(bias),是不同数据集在特定模型上预测值的期望与实际值之间的差值。如果平均预测值与实际值相差甚远,则偏差较高。高偏差导致算法无法正确表示输入和输出变量之间的相关关系。当模型具有较高的偏差时,则表示该模型过于简单,无法捕获数据的复杂性,因此无法拟合数据。
方差(variance),指的是不同数据集在特定模型上的预测值的方差。当模型在训练后的数据集上表现良好但在未训练的数据集(例如测试数据集或验证数据集)上表现不佳时,就会发生方差。 方差反映了预测值与实际值之间的分散程度。高方差会导致过度拟合,这表明该算法对训练数据中存在的随机噪声也进行了建模。当模型具有较高的方差时,该模型将变得非常复杂,并将“完美拟合”训练集的数据点。 当高方差模型遇到尚未学习的其他数据点时,就无法做出正确的预测。
图5显示了偏差和误差,其中蓝色点表示我们的预测值,红色点表示我们的真实值。可以看到,偏差越高,预测值离真实值越远;方差越高,预测值越分散。
2.2.用数学公式表示偏差和误差
我们用 Y Y Y表示我们要预测的值(样本真实值), X X X表示我们的自变量。考虑到样本数据其实是采样, Y Y Y并不是真实值,假设真实模型是 f f f,则有这样的关系: Y = f ( X ) + ϵ Y=f(X)+\epsilon Y=f(X)+ϵ,其中 ϵ \epsilon ϵ表示噪音,服从均值为0的正态分布,即 ϵ ∼ N ( μ , σ ϵ ) \epsilon\sim N(\mu,\sigma_\epsilon) ϵ∼N(μ,σϵ)。用 f ^ \hat f f^来表示我们的模型(即拟合函数),则我们的预测值为 f ^ ( X ) \hat f(X) f^(X),则在点 x x x处的平方误差的期望为:
E r r ( x ) = E [ ( Y − f ^ ( x ) ) 2 ] = E [ ( ϵ + f ( x ) − f ^ ( x ) ) 2 ] = E [ f ( x ) 2 ] + E [ f ^ ( x ) 2 ] + E ( ϵ 2 ) − 2 E [ f ( x ) ] E [ f ^ ( x ) ] − 2 E ( ϵ ) E [ f ( x ) ] − 2 E ( ϵ ) E [ f ^ ( x ) ] = f ( x ) 2 + ( E [ f ^ ( x ) ] ) 2 + V a r [ f ^ ( x ) ] − 2 f ( x ) E [ f ^ ( x ) ] + V a r [ ϵ ] + E ( ϵ ) = ( E [ f ^ ( x ) ] − f ( x ) ) 2 + E [ ( f ^ ( x ) − E [ f ^ ( x ) ] ) 2 ] + σ e 2 = B i a s 2 + V a r i a n c e + I r r e d u c i b l e E r r o r \begin{aligned}Err(x)& =E\left[(Y -\hat f(x))^2\right] = E\left[(\epsilon + f(x) -\hat f(x))^2\right]\\&=E[f(x)^2] + E[\hat f(x)^2] + E(\epsilon^2) -2E[f(x)]E[\hat f(x)]-2E(\epsilon)E[f(x)]-2E(\epsilon)E[\hat f(x)]\\& = f(x)^2+(E[\hat f(x)])^2 + Var[\hat f(x)] -2f(x)E[\hat f(x)] + Var[\epsilon] + E(\epsilon) \\& = \left(E[\hat{f}(x)]-f(x)\right)^2 + E\left[\left(\hat{f}(x)-E[\hat{f}(x)]\right)^2\right] +\sigma_e^2\\&= \mathrm{Bias}^2 + \mathrm{Variance} + \mathrm{Irreducible\ Error} \end{aligned} Err(x)=E[(Y−f^(x))2]=E[(ϵ+f(x)−f^(x))2]=E[f(x)2]+E[f^(x)2]+E(ϵ2)−2E[f(x)]E[f^(x)]−2E(ϵ)E[f(x)]−2E(ϵ)E[f^(x)]=f(x)2+(E[f^(x)])2+Var[f^(x)]−2f(x)E[f^(x)]+Var[ϵ]+E(ϵ)=(E[f^(x)]−f(x))2+E[(f^(x)−E[f^(x)])2]+σe2=Bias2+Variance+Irreducible Error
注意: f ( x ) , f ^ ( x ) , ϵ f(x),\hat f(x), \epsilon f(x),f^(x),ϵ三者独立,且 f ( x ) f(x) f(x)不是变量,是固定值。所以 E [ f ( x ) ] = f ( x ) , E [ f ( x ) 2 ] = f ( x ) 2 E[f(x)] = f(x),E[f(x)^2] = f(x)^2 E[f(x)]=f(x),E[f(x)2]=f(x)2。
即误差的期望值 = 预测值相对真实值的偏差的平方 + 模型预测值的方差 + 噪音的方差
上式中的第三项,为不可减少的误差,是真实模型和样本值的关系中的噪声项,任何模型都无法从根本上减少噪声项。 给定真实模型和无穷大数据进行校准,理论上可以将偏差项和方差项都减少到0。但是,在模型和有限数据不完善的现实情况下,需要在最小化偏差和最小化方差之间进行权衡 。
关于偏差和方差的更多内容可以参见:
偏差Bias和方差Variance–机器学习中的模型选择(中文)
Understanding the Bias-Variance Tradeoff(英文)
3.解决方法
模型的效果通常是:方差小,偏差小 > 方差小,偏差大 > 方差大,偏差小 > 方差大,偏差大。所以,我们尽量减少模型的偏差和方差。如果出现了欠拟合和过拟合的情况,我们应该怎么解决呢?
对于欠拟合而言,我们有如下解决方案:
- 增加新的特征,可以考虑加入进特征组合、高次特征,来增大假设空间
- 采用非线性模型,比如核SVM 、决策树、DNN等模型
- Boosting,Boosting 往往会有较小的 Bias,比如 Gradient Boosting 等
- 如果已正则化,尝试减少正则化程度 λ \lambda λ
对于过拟合而言,我们有如下解决方案:
- 交叉检验,通过交叉检验得到较优的模型参数
- 特征选择,减少特征数或使用较少的特征组合,对于按区间离散化的特征,增大划分的区间
- 正则化,常用的有 L1、L2 正则
- 如果已正则化,尝试增大正则化程度 λ \lambda λ
- 增加训练数据可以有限的避免过拟合
- Bagging,将多个弱学习器Bagging 一下效果会好很多,比如随机森林等
参考链接:
偏差Bias和方差Variance——机器学习中的模型选择
Understanding the Bias-Variance Tradeoff
机器学习防止欠拟合、过拟合方法