1 LRU 缓存介绍
LRU 算法全称是最近最少使用算法(Least Recently Use),是一种简单的缓存策略。顾名思义,LRU 算法会选出最近最少使用的数据进行淘汰。
那么什么是缓存呢?缓存专业点可以叫一种提高数据读取性能的技术,可以有效解决存储器性能和容量的矛盾,是一种空间换时间的设计思想,比如我们常见的内存是硬盘的缓存,Cache 是内存的缓存,浏览器本地存储是网络访问的缓存......
LRU 有许多应用场景,例如:
- 操作系统底层的内存管理。
- 缓存服务,例如 Redis,当数据满的时候就要淘汰掉长期不使用的 key,在 Redis 中用了一个类似的 LRU 算法,而不是严格的 LRU 算法。
- MySQL 的 Buffer Pool,也就是缓冲池,它的目的是为了减少磁盘 IO。它是一块连续的内存,当 Buffer Pool 满的时候就要淘汰很久没有被访问过的页。
2 Leetcode 真题
[146. LRU 缓存 [1]](https://leetcode.cn/problems/...),请你设计并实现一个满足 LRU (最近最少使用) 缓存约束的数据结构。
实现 LRUCache 类:
- LRUCache(int capacity) 以正整数作为容量 capacity 初始化 LRU 缓存。
- int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 。
- void put(int key, int value) 如果关键字 key 已经存在,则变更其数据值 value ;如果不存在,则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ,则应该逐出最久未使用的关键字。
函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。
示例:
输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]
解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1); // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废,缓存是 {1=1, 3=3}
lRUCache.get(2); // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废,缓存是 {4=4, 3=3}
lRUCache.get(1); // 返回 -1 (未找到)
lRUCache.get(3); // 返回 3
lRUCache.get(4); // 返回 43 题目分析
- 1.首先,题目中提到函数 get 和 put 必须以 O(1) 的平均时间复杂度运行,很自然地我们可以想到应该使用哈希表。
- 2.其次,当访问数据结构中的某个 key 时,需要将这个 key 更新为最近使用;另外如果 capacity 已满,需要删除访问时间最早的那条数据。这要求数据是有序的,并且可以支持在任意位置快速插入和删除元素,链表可以满足这个要求。
- 3.结合 1,2 两点来看,我们可以采用哈希表 + 链表的结构实现 LRU 缓存。
如上图所示,就是哈希表 + 链表实现的 LRU 缓存数据结构,有以下几个问题解释一下:
- 1.为什么这里要使用双向链表,而不是单向链表?
我们在找到了节点,需要删除节点的时候,如果使用单向链表的话,后驱节点的指针是直接能拿到的,但是这里要求时间复杂度是 O(1),要能够直接获取到前驱节点的指针,那么只能使用双向链表。 - 2.哈希表里面已经保存了 key ,那么链表中为什么还要存储 key 和 value 呢,只存入 value 不就行了?
当我们删除节点的时候,除了需要删除链表中的节点,还需要删除哈希表中的节点。删除哈希表中的节点需要知道 key,所以在链表的节点中需要存储 key 和 value,当删除链表节点时拿到 key,再根据 key 到哈希表中删除节点。 - 3.虚拟头节点和虚拟尾节点有什么用?
虚拟节点在链表中被广泛应用,又称为哨兵节点,通常不保存任何数据。使用虚拟节点我们可以统一处理链表中所有节点的插入删除操作,而不用考虑头尾两个节点的特殊情况。
4 代码实现
4.1 Golang
package main
import "fmt"
// LRU 数据结构
type LRUCache struct {
capacity int // 容量
size int // 已使用空间
head, tail *DLinkedNode // 头节点,尾节点
cache map[int]*DLinkedNode // 哈希表
}
// 双向链表数据结构
type DLinkedNode struct {
key, value int
prev, next *DLinkedNode // 前指针,后指针
}
// 创建一个新的节点
func initDLinkedNode(key, value int) *DLinkedNode {
return &DLinkedNode{
key: key,
value: value,
}
}
// 初始化 LRU 结构
func Constructor(capacity int) LRUCache {
l := LRUCache{
cache: map[int]*DLinkedNode{}, // 哈希表
head: initDLinkedNode(0, 0), // 虚拟头节点
tail: initDLinkedNode(0, 0), // 虚拟尾节点
capacity: capacity, // 容量
}
// 虚拟头节点和虚拟尾节点互连
l.head.next = l.tail
l.tail.prev = l.head
return l
}
// 获取元素
func (this *LRUCache) Get(key int) int {
// 如果没有在哈希表中找到 key
if _, ok := this.cache[key]; !ok {
return -1
}
// 如果 key 存在,先通过哈希表定位,再移到头部
node := this.cache[key]
this.moveToHead(node)
return node.value
}
// 插入元素
func (this *LRUCache) Put(key int, value int) {
// 先去哈希表中查询
// 如果 key 不存在,创建一个新的节点
if node, ok := this.cache[key]; !ok {
newNode := initDLinkedNode(key, value)
// 如果达到容量限制,链表删除尾部节点,哈希表删除元素
this.size++
if this.size > this.capacity {
// 得到删除的节点
removed := this.removeTail()
// 根据得到的 key 删除哈希表中的元素
delete(this.cache, removed.key)
// 减少已使用容量
this.size--
}
// 插入哈希表
this.cache[key] = newNode
// 插入链表
this.addToHead(newNode)
} else { // 如果 key 存在,先通过哈希表定位,再修改 value,并移到头部
node.value = value
this.moveToHead(node)
}
}
// 将节点添加到头部
func (this *LRUCache) addToHead(node *DLinkedNode) {
// 新节点指向前后节点
node.prev = this.head
node.next = this.head.next
// 前后节点指向新节点
this.head.next.prev = node
this.head.next = node
}
// 删除该节点
func (this *LRUCache) removeNode(node *DLinkedNode) {
// 修改该节点前后节点的指针,不再指向该节点
node.next.prev = node.prev
node.prev.next = node.next
}
// 移动到头部,也就是当前位置删除,再添加到头部
func (this *LRUCache) moveToHead(node *DLinkedNode) {
this.removeNode(node)
this.addToHead(node)
}
// 移除尾部节点,淘汰最久未使用的
func (this *LRUCache) removeTail() *DLinkedNode {
node := this.tail.prev // 虚拟尾节点的上一个才是真正的尾节点
this.removeNode(node)
return node
}
// 打印链表(解题不需要此方法,只是为了显示效果)
func (this *LRUCache) printDLinkedNode() {
p := this.head
for p != nil {
fmt.Printf("key: %d, value: %d\n", p.key, p.value)
p = p.next
}
}
func main() {
lru := Constructor(3)
fmt.Println("=========================== 插入 3 个节点 ===========================")
lru.Put(1, 100)
lru.Put(2, 200)
lru.Put(3, 300)
fmt.Println("=========================== 打印当前链表 ===========================")
lru.printDLinkedNode()
fmt.Println("=========================== 插入第 4 个节点,LRU 缓存淘汰尾部节点 ===========================")
lru.Put(4, 400)
lru.printDLinkedNode()
fmt.Println("=========================== 获取 key2 节点,更新 LRU 缓存,将会移动至链表头部 ===========================")
lru.Get(2)
lru.printDLinkedNode()
}
4.2 Java
import java.util.HashMap;
import java.util.Map;
public class LRUCache {
// 双向链表
class DLinkedNode {
int key;
int value;
DLinkedNode prev;
DLinkedNode next;
public DLinkedNode() {
}
public DLinkedNode(int key, int value) {
this.key = key;
this.value = value;
}
}
// 哈希表
private Map cache = new HashMap<>();
// 已使用空间
private int size;
// 容量
private int capacity;
// 头节点,尾节点
private DLinkedNode head, tail;
public LRUCache(int capacity) {
this.size = 0;
this.capacity = capacity;
// 使用虚拟头部和虚拟尾部节点
head = new DLinkedNode();
tail = new DLinkedNode();
// 虚拟头节点和虚拟尾节点互连
head.next = tail;
tail.prev = head;
}
// 获取元素
public int get(int key) {
DLinkedNode node = cache.get(key);
// 如果没有在哈希表中找到 key
if (node == null) {
return -1;
}
// 如果 key 存在,先通过哈希表定位,再移到头部
moveToHead(node);
return node.value;
}
// 插入元素
public void put(int key, int value) {
DLinkedNode node = cache.get(key);
if (node == null) {
// 如果 key 不存在,创建一个新的节点
DLinkedNode newNode = new DLinkedNode(key, value);
// 如果达到容量限制,链表删除尾部节点,哈希表删除元素
size++;
if (size > capacity) {
// 得到删除的节点
DLinkedNode removed = removeTail();
// 根据得到的 key 删除哈希表中的元素
cache.remove(removed.key);
// 减少已使用容量
size--;
}
// 插入哈希表
cache.put(key, newNode);
// 添加至双链表的头部
addToHead(newNode);
} else {
// 如果 key 存在,先通过哈希表定位,再修改 value,并移到头部
node.value = value;
moveToHead(node);
}
}
// 将节点添加到链表头部
private void addToHead(DLinkedNode node) {
// 新节点指向前后节点
node.prev = head;
node.next = head.next;
// 前后节点指向新节点
head.next.prev = node;
head.next = node;
}
// 删除节点
private void removeNode(DLinkedNode node) {
// 修改该节点前后节点的指针,不再指向该节点
node.prev.next = node.next;
node.next.prev = node.prev;
}
// 移动到头部,也就是当前位置删除,再添加到头部
private void moveToHead(DLinkedNode node) {
removeNode(node);
addToHead(node);
}
// 移除尾部节点,淘汰最久未使用的
private DLinkedNode removeTail() {
DLinkedNode res = tail.prev; // 虚拟尾节点,prev 才是此时真正的尾节点
removeNode(res);
return res;
}
// 打印链表(解题不需要此方法,只是为了显示效果)
private void printDLinkedNode() {
DLinkedNode p = this.head;
while (p != null) {
System.out.printf("key: %d, value: %d\n", p.key, p.value);
p = p.next;
}
}
public static void main(String[] args) {
LRUCache lru = new LRUCache(3);
System.out.println("=========================== 插入 3 个节点 ===========================");
lru.put(1, 100);
lru.put(2, 200);
lru.put(3, 300);
System.out.println("=========================== 打印当前链表 ===========================");
lru.printDLinkedNode();
System.out.println("=========================== 插入第 4 个节点,LRU 缓存淘汰尾部节点 key1 ===========================");
lru.put(4, 400);
lru.printDLinkedNode();
System.out.println("=========================== 获取 key2 的节点,更新 LRU 缓存,将会移动至链表头部 ===========================");
lru.get(2);
lru.printDLinkedNode();
}
} 4.3 运行结果
代码运行的返回结果如下,其中头尾两个 key=0, value=0 的节点是虚拟节点,请忽略。
=========================== 插入 3 个节点 ===========================
=========================== 打印当前链表 ===========================
key: 0, value: 0
key: 3, value: 300
key: 2, value: 200
key: 1, value: 100
key: 0, value: 0
=========================== 插入第 4 个节点,LRU 缓存淘汰尾部节点 ===========================
key: 0, value: 0
key: 4, value: 400
key: 3, value: 300
key: 2, value: 200
key: 0, value: 0
=========================== 获取 key2 节点,更新 LRU 缓存,将会移动至链表头部 ===========================
key: 0, value: 0
key: 2, value: 200
key: 4, value: 400
key: 3, value: 300
key: 0, value: 0
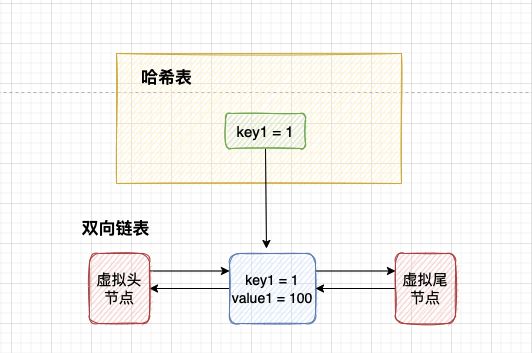
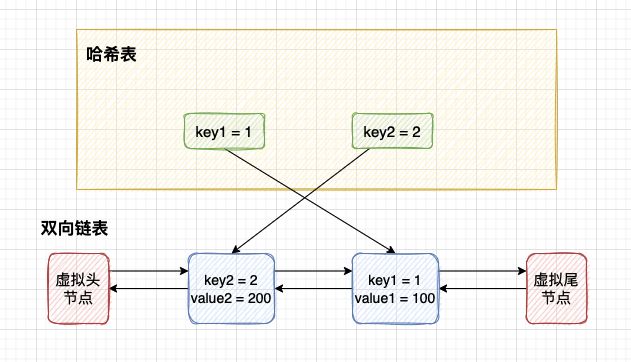
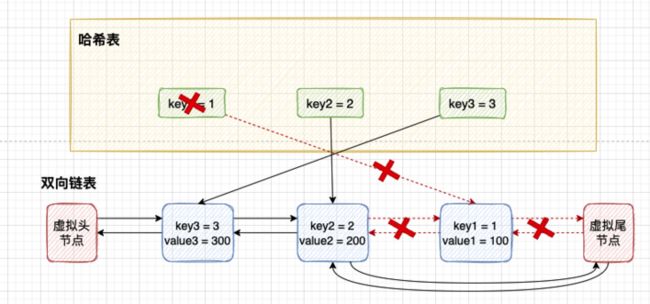
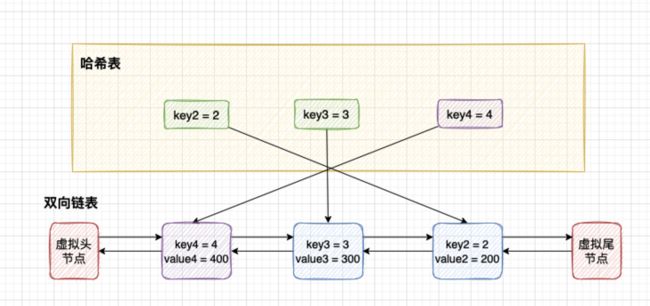
5 测试案例示意图
第 1 步:初始化数据结构。
第 2 步:插入节点 key1。
第 3 步:插入节点 key2。 此时 key2 插入到链表头部。
第 4 步:插入节点 key3。 此时 key3 插入到链表头部。
第 5 步:插入节点 key4。当前 capacity 容量达到上限(3),分为 2 步:
使用 removeTail() 方法删除链表尾部的节点 key1,从 removeTail() 方法的返回值得到 node,再根据 node.key 得到 key1,然后去哈希表删除节点 key1。
然后插入节点 key4,此时 key4 在链表头部。
第 6 步:读取 key2 的值,将 key2 移动到链表头部。
6 参考资料
- [1] 146. LRU 缓存: https://leetcode.cn/problems/...
- [2] 以Leetcode第146题为例学习LRU缓存算法: https://mp.weixin.qq.com/s/nI...
- [3] 从leetcode真题讲解手写LRU算法: http://www.xiaojieboshi.com/%...
- [4] LRU缓存机制: https://leetcode.cn/problems/...
- [5] Java集合系列之LinkedHashMap: https://juejin.cn/post/684490...
- [6] LinkedHashMap基本原理和用法&使用实现简单缓存: https://www.cnblogs.com/myser...
- [7] LRU算法及其优化策略——算法篇: https://juejin.cn/post/684490...
7 欢迎关注
![]()