高等数学笔记-乐经良老师-第十章-曲线积分和曲面积分
高等数学笔记-乐经良老师
第十章 曲线积分和曲面积分
第一节 第一类曲线积分和曲面积分
一、数量值函数的曲线积分
01 概念
问题:怎样求一段曲线弧状的质线的质量?
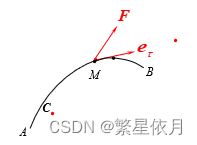
设 x y xy xy 平面的曲线弧为 C C C,端点 A , B A,B A,B,其上 ( x , y ) (x,y) (x,y) 处的线密度为 μ ( x , y ) \mu(x,y) μ(x,y)
用分点 A 1 , A 2 , ⋯ , A n − 1 A_{1}, A_{2}, \cdots, A_{n-1} A1,A2,⋯,An−1,将 C C C 分成 n n n 小段,记 A 0 = A , A n = B A_{0}=A, A_{n}=B A0=A,An=B,
第 i i i 个小弧段 A i − 1 A i A_{i-1} A_{i} Ai−1Ai 的长度为 Δ s i \Delta s_{i} Δsi 第 i i i 个小弧段上任取一点 ( ξ i , η i ) \left(\xi_{i}, \eta_{i}\right) (ξi,ηi),
小弧段的质量近似 μ ( ξ i , η i ) Δ s i \mu\left(\xi_{i}, \eta_{i}\right) \Delta s_{i} μ(ξi,ηi)Δsi,质线的质量近似为 ∑ i = 1 n μ ( ξ i , η i ) Δ s i \sum \limits_{i=1}^{n} \mu\left(\xi_{i}, \eta_{i}\right) \Delta s_{i} i=1∑nμ(ξi,ηi)Δsi
记 λ = max 1 ≤ i ≤ n Δ s i \lambda=\max \limits_{1 \leq i \leq n} \Delta s_{i} λ=1≤i≤nmaxΔsi,若极限 lim λ → 0 ∑ i = 1 n μ ( ξ i , η i ) Δ s i \lim \limits_{\lambda \rightarrow 0} \sum \limits_{i=1}^{n} \mu\left(\xi_{i}, \eta_{i}\right) \Delta s_{i} λ→0limi=1∑nμ(ξi,ηi)Δsi 存在,那么此极限给出了弧状质线的质量。
试一试
去掉物理背景,取代密度 μ ( x , y ) \mu(x, y) μ(x,y) 为定义在曲线 C C C 上的有界函数 f ( x , y ) f(x, y) f(x,y),
给出数量值函数曲线积分的定义: ∫ C f ( x , y ) d s = lim λ → 0 ∑ i = 1 n f ( ξ i , η i ) Δ s i \int \limits_{C} f(x, y) d s=\lim \limits_{\lambda \rightarrow 0} \sum \limits_{i=1}^{n} f\left(\xi_{i}, \eta_{i}\right) \Delta s_{i} C∫f(x,y)ds=λ→0limi=1∑nf(ξi,ηi)Δsi .
数量值曲线积分又称第一类曲线积分。
几何问题:求一块柱面的面
设 C C C 是 x y x y xy 平面上曲线, S S S 是以 C C C 为准线,母线垂直 x y x y xy 平面的柱面,
柱面高度为 f ( x , y ) f(x, y) f(x,y) ,求 x y x y xy 平面以上这部分柱面 S S S 的面积
结论: A = ∫ C f ( x , y ) d s A=\int \limits_{C} f(x, y) d s A=C∫f(x,y)ds (曲线积分的几何意义)
02 性质
(1) 与曲线方向无关:若曲线 C C C,则
∫ A B f ( x , y ) d s = ∫ B A f ( x , y ) d s \int \limits_{A B} f(x, y) d s=\int \limits_{B A} f(x, y) d s AB∫f(x,y)ds=BA∫f(x,y)ds
(2) 线性:
∫ C [ α f ( x , y ) + β g ( x , y ) ] d s = α ∫ C f ( x , y ) d s + β ∫ C g ( x , y ) d s \int \limits_{C}[\alpha f(x, y)+\beta g(x, y)] d s=\alpha \int_{C} f(x, y) d s+\beta \int_{C} g(x, y) d s C∫[αf(x,y)+βg(x,y)]ds=α∫Cf(x,y)ds+β∫Cg(x,y)ds
(3) 可加性:设曲线段 C 1 C_{1} C1 与 C 2 C_{2} C2 首尾相接成曲线 C C C
∫ C f ( x , y ) d s = ∫ C 1 f ( x , y ) d s + ∫ C 2 f ( x , y ) d s \int \limits_{C} f(x, y) d s=\int_{C_{1}} f(x, y) d s+\int_{C_{2}} f(x, y) d s C∫f(x,y)ds=∫C1f(x,y)ds+∫C2f(x,y)ds
(4) 中值定理:设函数 f f f 在光滑曲线段 C C C 上连续,则存在 ( ξ , η ) ∈ C (\xi, \eta) \in C (ξ,η)∈C,使得
∫ C f ( x , y ) d s = f ( ξ , η ) ⋅ s c ( S c 为 曲 线 段 C 的 长 度 ) \int \limits_{C} f(x, y) d s=f(\xi, \eta) \cdot s_{c}\quad( S_{c} 为曲线段 C 的长度) C∫f(x,y)ds=f(ξ,η)⋅sc(Sc为曲线段C的长度)
二、数量值函数曲线积分的计算
设函数 f ( x , y ) f(x,y) f(x,y) 在曲线 C C C 上连续, C C C 的参数方程为 { x = x ( t ) y = y ( t ) t ∈ [ α , β ] \left\{\begin{array}{l}x=x(t) \\ y=y(t)\end{array} \quad t \in[\alpha, \beta]\right. {x=x(t)y=y(t)t∈[α,β] ,
其中 x ( t ) , y ( t ) x(t),y(t) x(t),y(t) 均有连续导数。那么可得:
∫ C f ( x , y ) d s = ∫ α β f ( x ( t ) , y ( t ) ) x ′ 2 ( t ) + y ′ 2 ( t ) d t ( x ′ 2 ( t ) + y ′ 2 ( t ) d t 为 弧 微 分 d s ) \int \limits_{C} f(x, y) d s=\int_{\alpha}^{\beta} f(x(t), y(t)) \sqrt{x^{\prime 2}(t)+y^{\prime 2}(t)} d t\quad(\sqrt{x^{\prime 2}(t)+y^{\prime 2}(t)} d t\ \ 为弧微分\ ds) C∫f(x,y)ds=∫αβf(x(t),y(t))x′2(t)+y′2(t)dt(x′2(t)+y′2(t)dt 为弧微分 ds)
由于这积分中的 d s d s ds 是弧长,取正值,故右端积分限应 α ≤ β \alpha \leq \beta α≤β
当曲线形式为 y = y ( x ) , x ∈ [ a , b ] y=y(x),\quad x\in[a,b] y=y(x),x∈[a,b]
∫ C f ( x , y ) d s = ∫ a b f ( x , y ( x ) ) 1 + y ′ 2 ( x ) d x \int \limits_{C} f(x, y) d s=\int_{a}^{b} f(x, y(x)) \sqrt{1+y^{\prime 2}(x)} d x C∫f(x,y)ds=∫abf(x,y(x))1+y′2(x)dx
回顾在极坐标 r = r ( θ ) r=r(\theta) r=r(θ), d s = r 2 + r ′ 2 d θ ds=\sqrt{r^2+r'^2}d\theta ds=r2+r′2dθ .
思考或猜测
对于空间曲线 L L L:
x = x ( t ) , y = y ( t ) , z = z ( t ) , t ∈ [ α , β ] x=x(t), y=y(t), z=z(t), \quad t \in[\alpha, \beta] x=x(t),y=y(t),z=z(t),t∈[α,β]
第一型曲线积分 ∫ L f ( x , y , z ) d s \int \limits_{L} f(x, y, z) d s L∫f(x,y,z)ds 的概念与计算式任何?
三、数量值函数的曲面积分
问题:怎样求一块曲面的质量?
设函数 f ( x , y , z ) f(x, y, z) f(x,y,z) 定义在分片光滑的曲面 S S S 上,试将 f ( x , y , z ) f(x, y, z) f(x,y,z) 视为面密度,
采用分割、求和、取极限的来求这曲面质量,从而导出第一型曲面积分的定义,
其记号为 ∬ S f ( x , y , z ) d S \iint \limits_{S} f(x, y, z) d S S∬f(x,y,z)dS .
第一型曲面积分有类于第一型曲线积分的性质,如线性和可加性。
四、第一类曲面积分计算法
回顾在重积分一章,我们已经得知:曲线 S S S 为 z = z ( x , y ) , ( x , y ) ∈ D z=z(x,y),\quad(x,y)\in D z=z(x,y),(x,y)∈D .
则有, d S = 1 + z x 2 + z y 2 d x d y d S=\sqrt{1+z_{x}^{2}+z_{y}^{2}}\ d x d y dS=1+zx2+zy2 dxdy .
从而, ∬ S f ( x , y , z ) d S = ∬ D f ( x , y , z ( x , y ) ) 1 + z x 2 + z y 2 d x d y \iint \limits_{S} f(x, y, z) d S=\iint \limits_{D} f(x, y, z(x, y)) \sqrt{1+z_{x}^{2}+z_{y}^{2}} d x d y S∬f(x,y,z)dS=D∬f(x,y,z(x,y))1+zx2+zy2dxdy .
公式的导出:
∣ cos φ ∣ = 1 1 + z x 2 + z y 2 |\cos \varphi|=\frac{1}{\sqrt{1+z_{x}^{2}+z_{y}^{2}}} ∣cosφ∣=1+zx2+zy21
φ \varphi φ 是 d S dS dS 上的法向量与 z z z 方向的夹角。
那么当曲面 S S S 为 { x = x ( u , v ) y = y ( u , v ) ( u , v ) ∈ D z = z ( u , v ) \left\{\begin{array}{l}x=x(u, v) \\ y=y(u, v) \quad(u, v) \in D \\ z=z(u, v)\end{array}\right. ⎩⎨⎧x=x(u,v)y=y(u,v)(u,v)∈Dz=z(u,v) .
注意 d S dS dS 的法向量: ( x u , y u , z u ) × ( x v , y v , z v ) \left(x_{u}, y_{u}, z_{u}\right) \times\left(x_{v}, y_{v}, z_{v}\right) (xu,yu,zu)×(xv,yv,zv) .
= ( ∣ y u z u y v z v ∣ , ∣ z u x u z v x v ∣ , ∣ x u y u x v y v ∣ ) = 记为 ( A , B , C ) ⇒ d S = A 2 + B 2 + C 2 ∣ C ∣ d x d y =\left(\left|\begin{array}{cc} y_{u} & z_{u} \\ y_{v} & z_{v} \end{array}\right|,\left|\begin{array}{ll} z_{u} & x_{u} \\ z_{v} & x_{v} \end{array}\right|,\left|\begin{array}{ll} x_{u} & y_{u} \\ x_{v} & y_{v} \end{array}\right|\right) \stackrel{\text { 记为 }}{=}(A, B, C)\quad \Rightarrow \quad d S=\frac{\sqrt{A^{2}+B^{2}+C^{2}}}{|C|} d x d y =(∣∣∣∣yuyvzuzv∣∣∣∣,∣∣∣∣zuzvxuxv∣∣∣∣,∣∣∣∣xuxvyuyv∣∣∣∣)= 记为 (A,B,C)⇒dS=∣C∣A2+B2+C2dxdy
回顾 d x d y dxdy dxdy 与 d u d v dudv dudv 关系, d x d y = ∣ C ∣ d u d v dxdy=|C|dudv dxdy=∣C∣dudv,故得: d S = A 2 + B 2 + C 2 d u d v d S=\sqrt{A^{2}+B^{2}+C^{2}} d u d v dS=A2+B2+C2dudv .
其中, A = ∂ ( y , z ) ∂ ( u , v ) , B = ∂ ( z , x ) ∂ ( u , v ) , C = ∂ ( x , y ) ∂ ( u , v ) A=\frac{\partial(y, z)}{\partial(u, v)}, \quad B=\frac{\partial(z, x)}{\partial(u, v)}, \quad C=\frac{\partial(x, y)}{\partial(u, v)} A=∂(u,v)∂(y,z),B=∂(u,v)∂(z,x),C=∂(u,v)∂(x,y) .
因此曲面积分计算公式为:
∬ S f ( x , y , z ) d S = ∬ D f [ x ( u , v ) , y ( u , v ) , z ( u , v ) ] A 2 + B 2 + C 2 d u d v \iint \limits_{S} f(x, y, z) d S=\iint \limits_{D} f[x(u, v), y(u, v), z(u, v)] \sqrt{A^{2}+B^{2}+C^{2}} d u d v S∬f(x,y,z)dS=D∬f[x(u,v),y(u,v),z(u,v)]A2+B2+C2dudv
第二节 第二类曲线积分和曲面积分
一、向量值函数曲线积分的概念
01 例子与概念
问题:设在光滑平面曲线 C C C 上有连续的作用力 F ( x , y ) = ( P ( x , y ) , Q ( x , y ) ) F(x,y)=(P(x,y),Q(x,y)) F(x,y)=(P(x,y),Q(x,y)),
求 F F F 作用于 C C C 上质点从起点 A A A 移动到终点 B B B 所做的功为多少?
考察质点在 C C C 上任一 M M M 处移动一段弧微元所做的功:
d W = F ⋅ e τ d s ⇒ W = ∫ C F ⋅ e τ d s 由 于 单 位 切 向 量 e τ = ( d x d s , d y d s ) ⇒ e τ d s = ( d x , d y ) 于 是 W = ∫ C F ⋅ e τ d s = ∫ C P d x + Q d y ( 给 出 两 类 曲 线 积 分 关 系 ) \begin{aligned} & d W=F \cdot e_{\tau} d s \quad\Rightarrow\quad W=\int \limits_{C} F \cdot e_{\tau} d s\\ & 由于单位切向量\quad e_{\tau}=(\frac{dx}{ds},\frac{dy}{ds})\quad\Rightarrow\quad e_{\tau}ds=(dx,dy)\\ & 于是\quad W=\int \limits_{C} F \cdot e_{\tau} d s=\int \limits_{C} P d x+Q d y \quad(给出两类曲线积分关系) \end{aligned} dW=F⋅eτds⇒W=C∫F⋅eτds由于单位切向量eτ=(dsdx,dsdy)⇒eτds=(dx,dy)于是W=C∫F⋅eτds=C∫Pdx+Qdy(给出两类曲线积分关系)
向量函数 F = ( P ( x , y ) , Q ( x , y ) ) F=(P(x,y),Q(x,y)) F=(P(x,y),Q(x,y)) 在曲线 C C C 切方向 ( A 到 B ) (A到B) (A到B) 上投影的曲线积分写成: ∫ C P d x + Q d y \int_{C} P d x+Q d y ∫CPdx+Qdy .
称为向量值函数曲线积分或第二类曲线积分。
记 r = ( x , y ) r=(x,y) r=(x,y),可将其写成 ∫ C F ⋅ d r ( 向 量 形 式 ) \int \limits_C F\cdot dr\quad(向量形式) C∫F⋅dr(向量形式) .
02 性质
与第一类曲线积分不同,第二类曲线积分与曲线方向有关
∫ A B P d x + Q d y = − ∫ B A P d x + Q d y \int \limits_{A B} P d x+Q d y=-\int \limits_{B A} P d x+Q d y AB∫Pdx+Qdy=−BA∫Pdx+Qdy
还有与其他积分类似的性质,例如线性与可加性。
注意两点:
(1) 两种曲线积分形式的不同
(2) Q = 0 或 P = 0 Q=0 \ 或 \ P=0 Q=0 或 P=0, ∫ C P d x 或 ∫ C Q d y 仍 是 第 二 类 \int_{C} P d x \ 或 \ \int \limits_{C} Q d y\ 仍是第二类 ∫CPdx 或 C∫Qdy 仍是第二类 .
二、向量值函数曲线积分的计算
若曲线 C C C: A B AB AB 为 { x = x ( t ) y = y ( t ) t ∈ [ α , β ] \left\{\begin{array}{l}x=x(t) \\ y=y(t)\end{array} \quad t \in[\alpha, \beta]\right. {x=x(t)y=y(t)t∈[α,β] ,起点 A A A 对应 α \alpha α,终点 B B B 对应 β \beta β .
考察 ∫ C P d x + Q d y = ∫ C F ⋅ e τ d s \int \limits_{C} P d x+Q d y=\int \limits_{C} F \cdot e_{\tau} d s C∫Pdx+Qdy=C∫F⋅eτds,由于
F = ( P ( x , y ) , Q ( x , y ) ) = ( P ( x ( t ) , y ( t ) ) , Q ( x ( t ) , y ( t ) ) ) e τ d s = ( d x , d y ) = ( x ′ ( t ) d t , y ′ ( t ) d t ) F=(P(x, y), Q(x, y))=(P(x(t), y(t)), Q(x(t), y(t))) e_{\tau} d s=(d x, d y)=\left(x^{\prime}(t) d t, y^{\prime}(t) d t\right) F=(P(x,y),Q(x,y))=(P(x(t),y(t)),Q(x(t),y(t)))eτds=(dx,dy)=(x′(t)dt,y′(t)dt)
故得计算式:
∫ C P d x + Q d y = ∫ α β [ P ( x ( t ) , y ( t ) ) x ′ ( t ) + Q ( x ( t ) , y ( t ) ) y ′ ( t ) ] d t \int \limits_{C} P d x+Q d y=\int_{\alpha}^{\beta}\left[P(x(t), y(t)) x^{\prime}(t)+Q(x(t), y(t)) y^{\prime}(t)\right] d t C∫Pdx+Qdy=∫αβ[P(x(t),y(t))x′(t)+Q(x(t),y(t))y′(t)]dt
思考或猜测:
空间曲线 L = A B : x = x ( t ) , y = y ( t ) , z = z ( t ) , t ∈ [ α , β ] L=A B \ : \ x=x(t), y=y(t), z=z(t) , t \in[\alpha, \beta] L=AB : x=x(t),y=y(t),z=z(t),t∈[α,β] ( 起点 A A A 对应 α \alpha α, 终点 B B B 对应 β \beta β ),
则第二类曲线积分 ∫ L P d x + Q d y + R d z \int \limits_{L} P d x+Q d y+R d z L∫Pdx+Qdy+Rdz 如何引进和计算。
三、向量值函数曲面积分
01 双侧曲面
设 S S S 是一光滑曲面, n n n 是起点 P P P 在 S S S 上的任一法向量,
若 P P P 在 S S S 上沿任何曲线连续变动而不越过曲面边界回到起始位置时,
法向量 n n n 总是保持原来的指向,则称 S S S 是双侧曲面 ( 莫比乌斯面不是双侧曲面 ) 。
常选定双侧曲面 S S S 一侧方向为正向,称为正侧,记为 S + S^+ S+ ;而封闭曲面通常取外侧为正侧。
02 概念与性质
(1) 例子与概念
设均匀流体具有连续的速度 v = ( P , Q , R ) v=(P, Q, R) v=(P,Q,R),这里 P , Q , R P, Q, R P,Q,R 是 x , y , z x, y, z x,y,z 的函数,流体自曲面 S S S 的负侧流向正侧,求单位时间通过 S S S 的流量
在曲面微元 d S d S dS 上,有
d Φ = v ⋅ n 0 d S ( n 0 是单位外法向量) ⇒ Φ = ∬ S v ⋅ n 0 d S d \Phi=\boldsymbol{v} \cdot \boldsymbol{n}^{0} d S \quad\left(\boldsymbol{n}^{0}\right. \text { 是单位外法向量) } \Rightarrow \Phi=\iint_{S} \boldsymbol{v} \cdot \boldsymbol{n}^{0} d S dΦ=v⋅n0dS(n0 是单位外法向量) ⇒Φ=∬Sv⋅n0dS
若去掉问题的物理背景,对向量函数 F = ( P , Q , R ) F=(P, Q, R) F=(P,Q,R)
可以引进积分
∬ S F ⋅ n 0 d S ( n 0 d S 记 为 d S , 定 侧 曲 面 微 元 ) \iint_{S} \boldsymbol{F} \cdot \boldsymbol{n}^{0} d S\quad(\ \boldsymbol{n}^{0} d S记为\ dS,定侧曲面微元\ ) ∬SF⋅n0dS( n0dS记为 dS,定侧曲面微元 )
记单位正侧法向量 n 0 = ( cos α , cos β , cos γ ) \boldsymbol{n}^{0}=(\cos \alpha, \cos \beta, \cos \gamma) n0=(cosα,cosβ,cosγ), 那么
∬ S F ⋅ n 0 d S = ∬ S ( P cos α + Q cos β + R cos γ ) d S \iint_{S} \boldsymbol{F} \cdot \boldsymbol{n}^{0} d S=\iint_{S}(P \cos \alpha+Q \cos \beta+R \cos \gamma) d S ∬SF⋅n0dS=∬S(Pcosα+Qcosβ+Rcosγ)dS
而 cos γ d S \cos \gamma d S cosγdS 是 d S d S dS 在 x y x y xy 平面上的投影,是 x y x y xy 平面上面积 微元,可记为 d x d y d x d y dxdy ,
同样 cos α d S , cos β d S \cos \alpha d S, \cos \beta d S cosαdS,cosβdS 分别记为 d y d z d y d z dydz 和 d z d x d z d x dzdx, 于是又可将上述积分记为
∬ S F ⋅ n 0 d S = ∬ S + P d y d z + Q d z d x + R d x d y \iint \limits_{S} \boldsymbol{F} \cdot \boldsymbol{n}^{0} d S=\iint \limits_{S^{+}} P d y d z+Q d z d x+R d x d y S∬F⋅n0dS=S+∬Pdydz+Qdzdx+Rdxdy
上式的右端形式称为向量值函数曲面积分或第二类曲面积分,从而
∬ S + P d y d z + Q d z d x + R d x d y = ∬ S ( P cos α + Q cos β + R cos γ ) d S \iint \limits_{S^{+}} P d y d z+Q d z d x+R d x d y =\iint \limits_{S}(P \cos \alpha+Q \cos \beta+R \cos \gamma) d S S+∬Pdydz+Qdzdx+Rdxdy=S∬(Pcosα+Qcosβ+Rcosγ)dS
( 两型曲面积分的关系 )
(2) 性质
第二类曲面积分与在曲面哪一侧积分有关
∬ S − P d y d z + Q d z d x + R d x d y = − ∬ S + P d y d z + Q d z d x + R d x d y \iint \limits_{S^{-}} P d y d z+Q d z d x +R d x d y =-\iint \limits_{S^{+}} P d y d z+Q d z d x+R d x d y S−∬Pdydz+Qdzdx+Rdxdy=−S+∬Pdydz+Qdzdx+Rdxdy
(试提出其他性质)
03 计算法
若曲面方程为
{ x = x ( u , v ) , y = y ( u , v ) , ( u , v ) ∈ D z = z ( u , v ) , \left\{\begin{array}{l} x=x(u, v), \\ y=y(u, v), \quad(u, v) \in D \\ z=z(u, v), \end{array}\right. ⎩⎨⎧x=x(u,v),y=y(u,v),(u,v)∈Dz=z(u,v),
则其法向量为 ± ( A , B , C ) \pm(A, B, C) ±(A,B,C) ,故单位法向量为
( cos α , cos β , cos γ ) = ± 1 A 2 + B 2 + C 2 ( A , B , C ) (\cos \alpha, \cos \beta, \cos \gamma)=\pm \frac{1}{\sqrt{A^{2}+B^{2}+C^{2}}}(A, B, C) (cosα,cosβ,cosγ)=±A2+B2+C21(A,B,C)
而 d S = A 2 + B 2 + C 2 d u d v d S=\sqrt{A^{2}+B^{2}+C^{2}} d u d v dS=A2+B2+C2dudv , 导出计算式
∬ S + P d y d z + Q d z d x + R d x d y = ± ∬ D ( P A + Q B + R C ) d u d v \iint \limits_{S^{+}} P d y d z+Q d z d x+R d x d y=\pm \iint \limits_{D}(P A+Q B+R C) d u d v S+∬Pdydz+Qdzdx+Rdxdy=±D∬(PA+QB+RC)dudv
( 其中正负号选择依据积分一侧的法向量而定 )
特别当 z = z ( x , y ) , ( x , y ) ∈ D x y z=z(x, y),(x, y) \in D_{x y} z=z(x,y),(x,y)∈Dxy
∬ S + P d y d z + Q d z d x + R d x d y = ± ∬ D x y ( − P z x − Q z y + R ) d x d y \iint \limits_{S^{+}} P d y d z+Q d z d x+R d x d y=\pm \iint \limits_{D_{x y}}\left(-P z_{x}-Q z_{y}+R\right) d x d y S+∬Pdydz+Qdzdx+Rdxdy=±Dxy∬(−Pzx−Qzy+R)dxdy
则其法向量为 ± ( A , B , C ) \pm(A, B, C) ±(A,B,C) ,故单位法向量为
( cos α , cos β , cos γ ) = ± 1 A 2 + B 2 + C 2 ( A , B , C ) (\cos \alpha, \cos \beta, \cos \gamma)=\pm \frac{1}{\sqrt{A^{2}+B^{2}+C^{2}}}(A, B, C) (cosα,cosβ,cosγ)=±A2+B2+C21(A,B,C)
而 d S = A 2 + B 2 + C 2 d u d v d S=\sqrt{A^{2}+B^{2}+C^{2}} d u d v dS=A2+B2+C2dudv , 导出计算式
∬ S + P d y d z + Q d z d x + R d x d y = ± ∬ D ( P A + Q B + R C ) d u d v \iint_{S^{+}} P d y d z+Q d z d x+R d x d y=\pm \iint_{D}(P A+Q B+R C) d u d v ∬S+Pdydz+Qdzdx+Rdxdy=±∬D(PA+QB+RC)dudv
( 其中正负号选择依据积分一侧的法向量而定 )
特别当 z = z ( x , y ) , ( x , y ) ∈ D x y z=z(x, y),(x, y) \in D_{x y} z=z(x,y),(x,y)∈Dxy
∬ S + P d y d z + Q d z d x + R d x d y = ± ∬ D x y ( − P z x − Q z y + R ) d x d y \iint \limits_{S^{+}} P d y d z+Q d z d x+R d x d y=\pm \iint \limits_{D_{x y}}\left(-P z_{x}-Q z_{y}+R\right) d x d y S+∬Pdydz+Qdzdx+Rdxdy=±Dxy∬(−Pzx−Qzy+R)dxdy
例如:
∬ S + R ( x , y , z ) d x d y = ± ∬ D x y R ( x , y , z ( x , y ) ) d x d y \iint \limits_{S^{+}} R(x, y, z) d x d y=\pm \iint \limits_{D_{x y}} R(x, y, z(x, y)) d x d y S+∬R(x,y,z)dxdy=±Dxy∬R(x,y,z(x,y))dxdy
第三节 格林公式
一、格林公式
01 连通区域及其边界方向
(1) 连通
若 D D D 为平面区域,则 D D D 是连通的
(2) 单连通与复连通
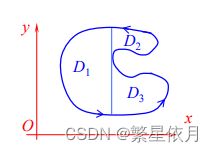
若连通域 D D D 内任意一条闭曲线所围成的区域都落在 D D D 内,则称 D D D 为单连通的,否则称 D D D 为复连通的
(3) 闭曲线的方向
当点沿区域边界朝一个方向前进时,区域总在它左侧,将此方向规定为闭曲线的正向,记为 C + C^+ C+ ;
与 C + C^+ C+ 相反的有向曲线记为 C − C^- C− 。
当平面闭曲线是单连通区域的边界时,依显然逆时针方向为其正向。
闭曲线上的第二类曲线积分未规定方向时,则沿正向积分。
02 格林公式
(1) 格林公式
设函数 P ( x , y ) , Q ( x , y ) P(x,y),Q(x,y) P(x,y),Q(x,y) 在有界区域 D D D 上有连续的偏导数, D D D 的边界 C C C 是分段光滑曲线,
则有公式:( 二重积分与在其边界上的第二型曲线积分的关系 )
常 常 写 成 ∮ 符 号 ⟶ ∫ C + P d x + Q d y = ∬ D ( ∂ Q ∂ x − ∂ P ∂ y ) d x d y 常常写成\oint符号 \longrightarrow \int \limits_{C^{+}} P d x+Q d y=\iint \limits_{D}\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) d x d y 常常写成∮符号⟶C+∫Pdx+Qdy=D∬(∂x∂Q−∂y∂P)dxdy
(2) 证明的思路
① 先考虑区域 D D D 是 x x x 型正规区域的情况
D = { ( x , y ) ∣ y 1 ( x ) ≤ y ≤ y 2 ( x ) , a ≤ x ≤ b } D=\left\{(x, y) \mid y_{1}(x) \leq y \leq y_{2}(x), a \leq x \leq b\right\} D={(x,y)∣y1(x)≤y≤y2(x),a≤x≤b}
证 ∮ C P d x = − ∬ D ∂ P ∂ y d x d y \oint \limits_{C} P d x=-\iint \limits_{D} \frac{\partial P}{\partial y} d x d y C∮Pdx=−D∬∂y∂Pdxdy
② 再考虑 D D D 为一般区域将 D D D 分割成几个正规区域
(3) 格林公式的向量形式
F = ( u ( x , y ) , v ( x , y ) ) n 0 ⃗ 为 C + 的 单 位 外 法 向 量 利 用 切 向 量 ⇒ n 0 = ( d y d s , − d x d s ) ∮ C + F ⋅ n 0 ⃗ d s = ∬ D ∇ ⋅ F d σ ( 格 林 公 式 的 向 量 形 式 ) \begin{aligned} & F=(u(x, y), v(x, y)) \quad \vec{n^0}\ 为\ C^+\ 的单位外法向量\\ & 利用切向量 \Rightarrow \boldsymbol{n}^{0}=\left(\frac{d y}{d s},-\frac{d x}{d s}\right)\\ & \oint_{C^{+}} F \cdot \vec{n^0} d s=\iint_{D} \nabla \cdot F d \sigma \quad(\ 格林公式的向量形式 \ ) \end{aligned} F=(u(x,y),v(x,y))n0 为 C+ 的单位外法向量利用切向量⇒n0=(dsdy,−dsdx)∮C+F⋅n0ds=∬D∇⋅Fdσ( 格林公式的向量形式 )
二、平面曲线积分与路径无关的条件
设函数 P ( x , y ) , Q ( x , y ) P(x,y),Q(x,y) P(x,y),Q(x,y) 上在单连通区域 D D D 有连续的偏导数,则下面的四个条件互相等价:
( 1 ) 在 D 内 的 任 一 条 逐 段 光 滑 的 闭 曲 线 C 上 , 即 ∮ C P d x + Q d y = 0 ( 2 ) 在 D 内 任 一 曲 线 积 分 ∫ C P d x + Q d y 与 路 径 无 关 ( 3 ) P d x + Q d y 是 某 个 函 数 u 的 全 微 分 , 即 d u = P d x + Q d y ( 此 时 称 u ( x , y ) 是 P d x + Q d y 的 原 函 数 ) ( 4 ) 在 D 内 恒 有 ∂ Q ∂ x = ∂ P ∂ y \begin{aligned} & (1)\ 在 D 内的任一条逐段光滑的闭曲线 C 上,即\ \oint \limits_{C} P d x+Q d y=0\\ & (2)\ 在 D 内任一曲线积分 \int \limits_{C} P d x+Q d y 与路径无关\\ & (3)\ P d x+Q d y 是某个函数 u 的全微分, 即\ d u=P d x+Q d y\\ &\quad\quad(此时称 u(x, y) 是 P d x+Q d y 的原函数)\\ & (4)\ 在 D 内恒有\ \frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y} \end{aligned} (1) 在D内的任一条逐段光滑的闭曲线C上,即 C∮Pdx+Qdy=0(2) 在D内任一曲线积分C∫Pdx+Qdy与路径无关(3) Pdx+Qdy是某个函数u的全微分,即 du=Pdx+Qdy(此时称u(x,y)是Pdx+Qdy的原函数)(4) 在D内恒有 ∂x∂Q=∂y∂P
三、全微分求积(全微分方程)
设函数 P ( x , y ) , Q ( x , y ) P(x, y), Q(x, y) P(x,y),Q(x,y) 上在单连通区域 D D D 有连续导数,且
∂ Q ∂ x = ∂ P ∂ y \frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y} ∂x∂Q=∂y∂P
则 P d x + Q d y P d x+Q d y Pdx+Qdy 是某个函数 u u u 的全微分:
u ( x , y ) = ∫ ( x 0 , y 0 ) ( x , y ) P d x + Q d y ← ( u 的 求 法 ) u(x, y)=\int_{\left(x_{0}, y_{0}\right)}^{(x, y)} P d x+Q d y\quad\leftarrow(u的求法) u(x,y)=∫(x0,y0)(x,y)Pdx+Qdy←(u的求法)
若 P ( x , y ) d x + Q ( x , y ) d y P(x, y) d x+Q(x, y) d y P(x,y)dx+Q(x,y)dy 是某二元函数的的全微分,称方程 P d x + Q d y = 0 P d x+Q d y=0 Pdx+Qdy=0 为全微分方程。
求出原函数 u u u,则解为 u = C u=C u=C 。
若 P ( x , y ) d x + Q ( x , y ) d y P(x, y) \mathrm{dx}+Q(x, y) \mathrm{d} \mathrm{y} P(x,y)dx+Q(x,y)dy 不是某二元函数的的全微分,方程 P d x + Q d y = 0 P d x+Q d y=0 Pdx+Qdy=0 的解法:
求出积分因子 μ \mu μ,使得方程化为 μ P ( x , y ) d x + μ Q ( x , y ) d y = 0 \mu P(x, y) d x+\mu Q(x, y) d y=0 μP(x,y)dx+μQ(x,y)dy=0 成为全微分方程。
常 用 积 分 因 子 : 1 x 2 , 1 y 2 , 1 x y , 1 x 2 y 2 , 1 x 2 + y 2 组 合 拼 凑 法 : 例 如 , 求 解 方 程 ① ( x − x 2 + y 2 ) d x = − y d y ( 分 组 结 合 凑 成 全 微 分 , 在 过 程 中 观 察 需 要 乘 何 因 子 ) ( x d x + y d y ) − x 2 + y 2 d x = 0 ⇒ d ( x 2 + y 2 ) − x 2 + y 2 d x = 0 乘 什 么 使 得 后 一 项 成 全 微 分 , 前 一 项 还 是 全 微 分 ? 若 将 x 2 + y 2 看 作 u , 应 乘 以 φ ( u ) 事 实 上 只 要 各 组 都 凑 成 全 微 分 , 方 程 就 解 出 来 了 求 解 方 程 ② y ( 1 + x y ) d x + x ( 1 − x y ) d y = 0 \begin{aligned} & 常用积分因子:\ \frac{1}{x^{2}}, \frac{1}{y^{2}}, \frac{1}{x y}, \frac{1}{x^{2} y^{2}}, \frac{1}{x^{2}+y^{2}}\\ & 组合拼凑法:\ \\ & 例如,求解方程①\ \left(x-\sqrt{x^{2}+y^{2}}\right) d x=-y d y\ \ (分组结合凑成全微分,在过程中观察需要乘何因子)\\ &\quad\quad\quad\quad\quad(x d x+y d y)-\sqrt{x^{2}+y^{2}} d x=0 \Rightarrow d\left(x^{2}+y^{2}\right)-\sqrt{x^{2}+y^{2}} d x=0 \\ & \quad\quad\quad\quad\quad乘什么使得后一项成全微分,前一项还是全微分?\ 若将 x^{2}+y^{2} 看作 u, 应乘以 \varphi(u)\\ & \quad\quad\quad\quad\quad事实上只要各组都凑成全微分,方程就解出来了\\ & 求解方程②\ \ y(1+x y) d x+x(1-x y) d y=0 \end{aligned} 常用积分因子: x21,y21,xy1,x2y21,x2+y21组合拼凑法: 例如,求解方程① (x−x2+y2)dx=−ydy (分组结合凑成全微分,在过程中观察需要乘何因子)(xdx+ydy)−x2+y2dx=0⇒d(x2+y2)−x2+y2dx=0乘什么使得后一项成全微分,前一项还是全微分? 若将x2+y2看作u,应乘以φ(u)事实上只要各组都凑成全微分,方程就解出来了求解方程② y(1+xy)dx+x(1−xy)dy=0
第四节 高斯公式
一、高斯公式
01 高斯公式
设函数 P ( x , y , z ) , Q ( x , y , z ) , R ( x , y , z ) P(x, y, z), Q(x, y, z), R(x, y, z) P(x,y,z),Q(x,y,z),R(x,y,z) 在空间有界必区域 Ω \Omega Ω 上有连续偏导数, Ω \Omega Ω 的边界是分片光滑的闭曲面,
则有公式:(三重积分与在其边界上的第二型曲面积分的关系)
∯ S + P d y d z + Q d z d x + R d x d y = ∭ Ω ( ∂ P ∂ x + ∂ Q ∂ y + ∂ R ∂ z ) d V \oiint \limits_{S^{+}} P d y d z+Q d z d x+R d x d y=\iiint \limits_{\Omega}\left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}\right) d V S+∬Pdydz+Qdzdx+Rdxdy=Ω∭(∂x∂P+∂y∂Q+∂z∂R)dV
02 证明的思路
类似格林公式的证明,先证明:
∯ S ∗ R d x d y = ∭ Ω ∂ R ∂ z d V \oiint \limits_{S^{*}} R d x d y=\iiint \limits_{\Omega} \frac{\partial R}{\partial z} d V S∗∬Rdxdy=Ω∭∂z∂RdV
(1) 考虑 Ω \Omega Ω 是 x y xy xy 型区域。
Ω = { ( x , y , z ) ∣ z 1 ( x , y ) ≤ z ≤ z 2 ( x , y ) , ( x , y ) ∈ D } \Omega=\left\{(x, y, z) \mid z_{1}(x, y) \leq z \leq z_{2}(x, y),(x, y) \in D\right\} Ω={(x,y,z)∣z1(x,y)≤z≤z2(x,y),(x,y)∈D}
(2) 再考虑 Ω \Omega Ω 是一般区域,将 Ω \Omega Ω 分割成几个正规区域应用①的结论,同理证明关于 P , Q P,Q P,Q 的等式。
03 高斯公式的向量形式
由于:
∬ S + P d y d z + Q d z d x + R d x d y = ∬ S F ⋅ n 0 d S ∭ Ω ( ∂ P ∂ x + ∂ Q ∂ y + ∂ R ∂ z ) d V = ∭ Ω ∇ ⋅ F d V \begin{aligned} &\iint \limits_{S^{+}} P d y d z+Q d z d x+R d x d y=\iint \limits_{S} \boldsymbol{F} \cdot \boldsymbol{n}^{0} d S \\ &\iiint \limits_{\Omega}\left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}\right) d V=\iiint \limits_{\Omega} \nabla \cdot \boldsymbol{F} d V \end{aligned} S+∬Pdydz+Qdzdx+Rdxdy=S∬F⋅n0dSΩ∭(∂x∂P+∂y∂Q+∂z∂R)dV=Ω∭∇⋅FdV
得到高斯公式的向量形式:
∬ S F ⋅ n 0 d S = ∬ Ω ∇ ⋅ F d V ( 高 斯 公 式 的 向 量 形 式 ) n 0 d S → d S 与 格 林 公 式 形 式 完 全 一 致 \begin{aligned} & \iint \limits_{S} \boldsymbol{F} \cdot \boldsymbol{n}^{0} dS =\iint \limits_{\Omega} \nabla \cdot \boldsymbol{F} d V \quad(\ 高斯公式的向量形式 \ )\\ & \quad\boldsymbol{n}^{0} dS\rightarrow dS\\ & \quad与格林公式形式完全一致 \end{aligned} S∬F⋅n0dS=Ω∬∇⋅FdV( 高斯公式的向量形式 )n0dS→dS与格林公式形式完全一致
二、通量与散度
若给定向量场 F = ( P ( x , y , z ) , Q ( x , y , z ) , R ( x , y , z ) ) F=(P(x, y, z), Q(x, y, z), R(x, y, z)) F=(P(x,y,z),Q(x,y,z),R(x,y,z)) 那么称曲面积分
Φ = ∬ S F ⋅ n 0 d S \Phi=\iint_{S} \boldsymbol{F} \cdot \boldsymbol{n}^{0} d S Φ=∬SF⋅n0dS
为向量函数 F F F 的通过定侧曲面 S S S 的通量,而称
div F = def ∇ ⋅ F = ∂ P ∂ x + ∂ Q ∂ y + ∂ R ∂ z \operatorname{div} \boldsymbol{F} \stackrel{\text { def }}{=} \nabla \cdot \boldsymbol{F}=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z} divF= def ∇⋅F=∂x∂P+∂y∂Q+∂z∂R
称为向量函数 F F F 的散度。
三、斯托克斯公式
01 斯托克斯公式
设双侧曲面 S S S 的边界为空间闭曲线 C 4 , C 4 C^{4}, C^{4} C4,C4 的 正方向与 S S S 的正侧成右手系。
设 S S S 是分片光滑的双侧曲面,闭曲线 C 4 C^{4} C4 是其边界,
向量值函数 F = ( P ( x , y , z ) , Q ( x , y , z ) , R ( x , y , z ) ) \boldsymbol{F}=(P(x, y, z), Q(x, y, z), R(x, y, z)) F=(P(x,y,z),Q(x,y,z),R(x,y,z)) 在包含 S S S 的空间区域内有连续偏导数,则
∮ C + P d x + Q d y + R d z = ∬ S + ( ∂ R ∂ y − ∂ Q ∂ z ) d y d z + ( ∂ P ∂ z − ∂ R ∂ x ) d z d x + ( ∂ Q ∂ x − ∂ P ∂ y ) d x d y \begin{aligned} \oint_{C^{+}} P d x &+Q d y+R d z \\ &=\iint_{S^{+}}\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right) d y d z+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right) d z d x+\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) d x d y \end{aligned} ∮C+Pdx+Qdy+Rdz=∬S+(∂y∂R−∂z∂Q)dydz+(∂z∂P−∂x∂R)dzdx+(∂x∂Q−∂y∂P)dxdy
借助行列式,公式可记为
∮ C + P d x + Q d y + R d z = ∬ S + ∣ d y d z d z d x d x d y ∂ ∂ x ∂ ∂ y ∂ ∂ z P Q R ∣ \oint_{C^{+}} P d x+Q d y+R d z=\iint_{S^{+}}\left|\begin{array}{ccc} d y d z & d z d x & d x d y \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ P & Q & R \end{array}\right| ∮C+Pdx+Qdy+Rdz=∬S+∣∣∣∣∣∣dydz∂x∂Pdzdx∂y∂Qdxdy∂z∂R∣∣∣∣∣∣
02 斯托克斯公式的向量形式
若记 r = ( x , y , z ) \boldsymbol{r}=(x, y, z) r=(x,y,z), 那么 d r = ( d x , d y , d z ) d \boldsymbol{r}=(d x, d y, d z) dr=(dx,dy,dz), 这样 Stokes公式可以写成形式
∮ C + F ⋅ d r = ∬ S + rot F ⋅ n 0 d S \oint_{C^{+}} \boldsymbol{F} \cdot d \boldsymbol{r}=\iint_{S^{+}} \operatorname{rot} \boldsymbol{F} \cdot \boldsymbol{n}^{0} d S ∮C+F⋅dr=∬S+rotF⋅n0dS
四、旋度
对向量场 F = ( P , Q , R ) \boldsymbol{F}=(P, Q, R) F=(P,Q,R) ,定义下列代数式为函数 F F F 的旋度。
rot F = ∇ × F = ( ∣ ∂ ∂ y ∂ ∂ z Q R ∣ , ∣ ∂ ∂ z ∂ ∂ x R P ∣ , ∣ ∂ ∂ x ∂ ∂ y P Q ∣ ) \operatorname{rot} \boldsymbol{F}=\nabla \times \boldsymbol{F}=\left(\left|\begin{array}{cc} \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ Q & R \end{array}\right|,\left|\begin{array}{cc} \frac{\partial}{\partial z} & \frac{\partial}{\partial x} \\ R & P \end{array}\right|,\left|\begin{array}{cc} \frac{\partial}{\partial x} & \frac{\partial}{\partial y} \\ P & Q \end{array}\right|\right) rotF=∇×F=(∣∣∣∣∂y∂Q∂z∂R∣∣∣∣,∣∣∣∣∂z∂R∂x∂P∣∣∣∣,∣∣∣∣∂x∂P∂y∂Q∣∣∣∣)
若 L L L 为 F F F 定义区域内的定向曲线,则称下列代数式为 F F F 沿 L L L 的环量。
∫ L F ⋅ d r = ∫ L P d x + Q d y + R d z \int_{L} \boldsymbol{F} \cdot d \boldsymbol{r}=\int_{L} P d x+Q d y+R d z ∫LF⋅dr=∫LPdx+Qdy+Rdz