同态加密简要介绍及研究现状

最近在学习同态加密相关技术，这是学习过程一点笔记，分享一下：
同态加密：基于数学难题的计算复杂性理论的密码学技术。对经过同态加密的数据进行处理得到一个输出，将这一输出进行解密，其结果与用同一方法处理未加密的原始数据得到的输出结果是一样的。

技术优势：使用同态加密技术，用户对密文进行运算后再解密得到的结果与直接对明文进行运算得到的结果一致，这一特性允许不可信第三方在没有私钥的情况下直接对密文进行运算，避免了第三方在运算过程中需要解密密文而导致的用户敏感信息泄露。使用同态加密技术，用户对密文进行运算后再解密得到的结果与直接对明文进行运算得到结果一致，这一特性允许不可信第三方再没有私钥情况下直接对密文进行运算，避免了运算过程需要解密密文而导致用户敏感信息泄露的可能。

example
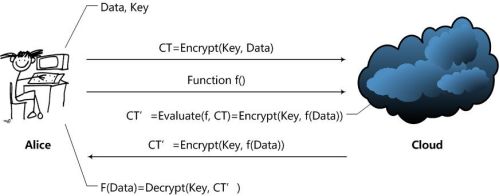
Alice通过Cloud，以Homomorphic Encryption（以下简称HE）处理数据的整个处理过程大致是这样的：
1.Alice对数据进行加密。并把加密后的数据发送给Cloud；
2.Alice向Cloud提交数据的处理方法，这里用函数f来表示；
3.Cloud在函数f下对数据进行处理，并且将处理后的结果发送给Alice；
4.Alice对数据进行解密，得到结果。

发展：
近年来研究热点之一是：如何构造高效的全同态加密方案。此处主要梳理了可验证全同态加密方案的研究进展。对比分析目前主流全同态加密库Helib，SEAL及TFHE的性能，梳理了同态加密技术的典型应用场景，指出了未来可能的研究发展方向。

1978年Rivest等人首次提出了隐私同态的概念，旨在构造一种支持密文检索的加密机制，2009年Gentry首次利用理想格给出了FHE方案的构造，该方案基于理想格上的有界编码问题与稀疏子集和问题。

其思路如下：明文空间为{0, 1}，首先构造一个对“新鲜”密文支持有限次多项式运算的类同态加密(Some What Homomorphic Encryption, SWHE)方案；然后基于稀疏子集和问题困难性假设变换私钥的形式，压缩解密电路，将其表示成关于私钥的次数足够低的多项式；最后在公钥中添加私钥的密文等辅助信息，用于对“新鲜”密文同态运算后生成的密文进行同态解密，降低其中包含的噪声，实现“自举”功能，达到对密文进行任意函数变换的目的，这一技术称为Bootstrapping(自举)技术。
Gentry提出的这种构造模式被称为Gentry体制，此后全同态加密技术发展迅速，分为两条研究主线，一种是按照Gentry的思路设计的FHE方案，另一种则为基于错误学习(Learning With Errors, LWE)问题或环上错误学习(Ring-LWE, RLWE)问题实现的FHE方案。下面，本文主要分析近年来同态加密技术的一些新进展并提出未来值得关注的几个发展方向。
同态加密的特点：

同态加密分类：
按照各同态加密方案允许密文计算的种类和次数，可以将其分为3类：
部分同态加密(Partial Homomorphic Encryption, PHE)方案、类同态加密方案和全同态加密方案。PHE仅满足加法或乘法的密文同态运算；SWHE可同时满足加法和乘法有限次的密文同态运算；FHE可同时满足加法和乘法无限次的密文同态运算。
同态性与延展性之间的相互矛盾，全同态加密无法实现IND-CCA2安全。因此，对全同态加密的研究仍然任重道远，且相应的主要聚焦于两个方面：一是提高FHE方案的效率；二是提高FHE方案的安全性。
研究阶段
全同态加密近十年来的研究可划分为3阶段：
第1是以Gentry的工作为基础构造的各类FHE方案，首先构造一个SWHE方案，然后通过Bootstrapping技术控制噪声增长实现全同态；

第2阶段是以Brakerski和Vaikuntanathan的工作为基础构造的基于LWE和RLWE错误学习(Learning With Errors, LWE)问题或环上错误学习(Ring-LWE, RLWE)的FHE方案，通过密钥交换(key switching)技术来解决维数膨胀的问题，通过模交换(Modulus Switching)技术来控制噪声，一定程度上摆脱了对Bootstrapping技术的依赖；

第3阶段是由Gentry等人构造的基于近似特征向量的GSW方案，该方案的同态运算全部为简单的矩阵运算，故不会出现维数膨胀的问题，该方案提供了一种构造FHE方案的新思路，将原先复杂的密文运算过程简化为了较为单纯的代数运算，更加便于理解。宋新霞等人对密文矩阵的本质及构造方法进行了研究，揭示了密文矩阵FHE与其它FHE之间的包含关系。
除上述按发展阶段划分外，FHE还可以依照所基于的困难问题来分类，主要有两种，一种是基于传统数论的困难问题，如整数上近似最大公约数(Approximate Greatest CommonDivisor, AGCD)问题，另一种是基于格密码学中的困难问题，如格上LWE问题和RLWE问题。

另外，近年还出现基于NTRU(Number Theory Research Unit)的FHE方案、基于身份和属性的FHE方案以及无噪声的FHE方案等诸多其他类型的FHE方案，李子臣等人通过格上的高斯抽象算法生成密钥对，然后利用Flattening技术构造了基于NTRU选择明文攻击可证明安全的全同态加密方案。为了解决NTRU在实现过程中的侧信道攻击安全隐患，杨亚涛等人对NTRU算法所有系数执行掩码操作，构造了能够有效防御差分能量攻击及相关能量攻击的NTRU全同态掩码防御方案。可以发现，近十年来建立在格密码学基础之上的FHE方案大量涌现，格密码作为后量子密码中颇具潜力的密码体制，使全同态加密技术在量子计算时代仍具有重要的应用价值。
2009年Gentry利用理想格给出了FHE方案的构造，基于理想格上的有界编码问题和稀疏子集问题。下面简要介绍Bootstrapping技术的原理。在使用Bootstrapping之前，我们已经可以进行有限次的密文同态运算，但是每进行一次同态运算后密文噪声都会相应增加，尤其是在进行同态乘运算时，密文噪声随运算次数呈指数形式增长，因此必须采取措施进行噪声控制。
噪声控制原理图

全同态加密噪声问题：构造无噪声的FHE方案成为当前全同态加密研究的一个重要思路。噪声的加入是为了保证FHE方案的安全性，但也带来了噪声控制的困扰，虽然无噪声的FHE方案被认为是不安全的，但该结论也并没有被严格证明，因此研究无噪声的FHE方案仍具有现实意义。提高全同台加密效率的解决方案：

Broadbent等人正式给出了量子同态加密(Quantum homomorphic encryption)的定义，即实现量子信息的加密以及密文的量子同态运算，此外作者还相应给出了量子信息中IND-CPA的定义。随后在CRYPTO2016中，Dulek等人基于所提出的架构，构造了第1个量子全同态加密(Quantum FHE, QFHE)方案，可以实现任意多项式级量子电路的密文运算。
可验证的同态加密：
同态签名和同态MAC都可以作为保护外包数据完整性和可靠性的有效手段，不过，同态签名可实现公开验证(Public verification)，同态MAC可实现私人验证(Private verification)。

同态加密的应用相关
已有学者基于CO-ACD(CO-ApproximateCommon Divisor)问题构造并实现了一个加法部分同态加密方案。公开了基于同态加密的签名方案，具体可以应用于匿名证书、电子投票和群签名中。
还有一种可验证计算正确性的全同态加密方案及其实现。以及一个包含密钥交换、模交换和噪声动态管理的同态加密库。
还有一种片上系统(System on Chip, SoC)的隐私保护验证方法，在验证时，参与验证的各方可以通过被加密的测试向量来验证IP核，以避免泄露不必要的信息。学者发明了用于读取同态运算指令的计算机可读存储器，实现了两个终端之间的同态加密通信。还公开了一种基于同态加密算法的个人图像安全检索方法，在不泄露用户检索信息和数据的前提下，实现图像的安全检索。
文献公开了一种云存储中基于同态加密的密文检索方法，保障了数据的隐私安全，同时使用树形结构来存储提高密文检索效率。
公开了一种基于同态加密的线性SVM(Support Vector Machine)模型训练算法，得以在云上训练密文SVM模型，从而避免泄露训练数据等隐私信息。还有一种基于全同态加密的生物特征认证技术，允许在密文状态下认证生物特征，从而避免用户信息泄露。
当前，同态加密已被应用在机器学习隐私保护领域，较有代表性的是Gilad-bachrach等人基于SEAL库提出的 隐私保护神经网络模型 Cryptonets，已较好地适用于小型神经网络。公开了一种基于加法同态的隐藏分散贷款额获取贷款总和的方法，这是多方安全计算的一个应用场景。
公开了一种基于同态加密的多值打包方案。文献公开了一种基于全同态加密的双方不经意传输方案。还有一种使用同态加密技术计算DNA编辑距离的方法，首先将DNA序列编码为字符串，然后在密文域实现两字符串间编辑距离的计算。
还公开了一种基于同态加密的智能电网用户售电方法，使用同态加密技术加密用户的真实购电需求，结合身份认证保护用户的购电信息不被电力公司等获取。
还有公开了一种基于同态加密技术生成条形码的技术，可以在密文域中根据从服务器接收到的生成请求来生成对应的标识码。
已有一种基于同态加密算法保护程序代码的方案及其实现，以增加程序代码安全性。文献公开了一种基于同态加密的通信技术，保障在通信过程中数据的计算安全和存储安全。
已有的同态加密函数库及其效率

目前已经有一些团队对FHE方案进行了软件实现，例如基于BGV方案的Helib、基于BFV方案的 SEAL、基于GSW方案的 TFHE等。下面分别分析Helib, SEAL和TFHE全同态加密库的运行效率。
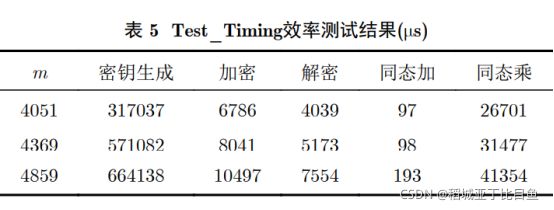
内存8 GB的Dell笔记本电脑进行效率测试，表5为level=2时Helib的运行效率，m表示模数。

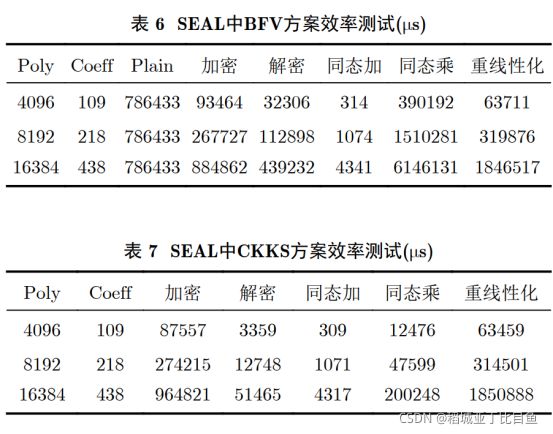
BFV方案在默认参数下的效率测试结果如表6所示，CKKS方案在默认参数下的效率测试结果如表7所示。其中Poly,Coeff和Plain为方案的3个主要参数，不同参数会影响方案的安全性、效率以及可进行同态运算的次数。

参考资料
链接：https://www.zhihu.com/question/27645858/answer/37598506 来源：知乎 作者：刘巍然-学酥
杨亚涛,赵阳,张卷美,黄洁润,高原.同态密码理论与应用进展[J].电子与信息学报,2021,43(02):475-487.