李宏毅老师《机器学习》课程笔记-2.2 为什么是“深度”学习？

注：本文是我学习李宏毅老师《机器学习》课程 2021/2022 的笔记（课程网站 ），文中图片均来自课程 PPT。欢迎交流和多多指教，谢谢！

Lecture2.2 why Deep Networks?

怎样让模型在训练集和测试集上的表现接近？

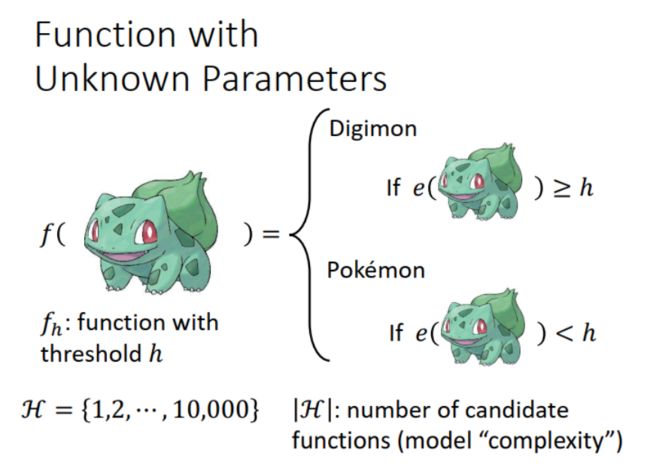
举例：宝可梦 ( Pokemon ) 与数码宝贝 ( Digimon ) 分类器。其中，H 表示所有可能的函数集（或者说参数集），代表了模型的复杂度。

理想：如果我们能收集到 全部的 数据，就可以得到一组最佳参数 $h^{all}$ 。

现实：我们只有训练数据，由此训练得到一组最佳参数 $h^{train}$ 。

希望：$h^{train}$ 在 全部 数据集上的表现 ( Loss )，能够接近 $h^{all}$ 的表现，如下图所示：

在实际中，我们很难收集到所有的数据，因此，用 $D_{test}$ 来代表 $D_{all}$ (“as the proxy of $D_{all}$”)。

是否可能 $L(h^{train},D_{train})<L(h^{all},D_{all})$ ？

有可能。比如二分类问题，正好就采样到了截然不同的样本点（不在分界线附近、容易分别的点），这样 $h_{train}$ 计算出来的 training loss 就小，可能小于 $h^{all}$ 在 all data 上的 loss。但如果把 $h_{train}$ 应用到 all data 上，还是有：$L(h^{train},D_{all})\ge L(h^{all},D_{all})$，因为在 all data 上，$h^{all}$ 是最优参数。

如果要让 $L(h^{train},D_{all})$ 接近 $L(h^{all},D_{all})$ ，就要 training data 是个 good sample。换言之，training data 要能反映 all data 的全部特点。具体条件如下图中公式所示，就是对于参数集 H 中的所有可能 $h$，$h$ 在 training data 和 all data 上计算得到的 Loss 相差不超过 $\delta /2$。

也就是说，我们希望 sample 得到的 training data 是 good sample，那么不妨先计算一下采到 bad sample 的概率是多少呢？

以下分析和讨论具有一般性 ( “very general” )，不考虑模型 ( model-agnostic )，不对数据分布做假设，可以使用任何 loss function。

下图中，每一个点代表的不是一条数据，而是一个训练数据集 ( training set )。蓝色点表示该训练集是 good sample，橙色点表示该训练集是 bad sample。

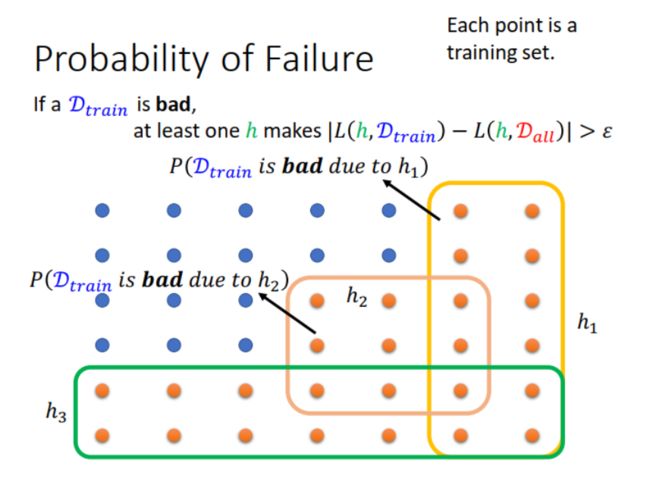
根据前面的假设，good sample 是指对于 H 中的所有 $h$，$|L(h,D_{train})-L(h,D_{all})|\le ϵ$ ，其中 $ϵ=\delta /2$。那么 bad sample 就是至少有一个 $h$ 不满足这个公式，也就是说某个 $h$ 导致一些 training set 成为 bad sample。例如图中黄色方框区域内的橙色点，因为 $h_1$ 不满足公式，这些 training sets 成为 bad samples。

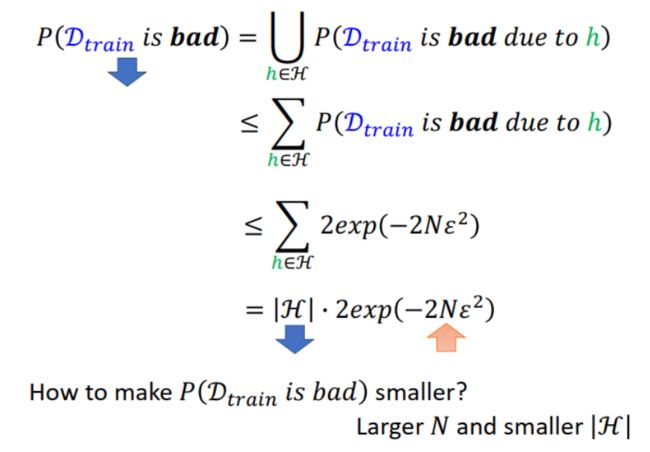
由此，可以求解 training set 是 bad sample 的概率，如下图所示。因为上图中 $h_1$, $h_2$ 和 $h_3$ 的区域有部分重合，所以概率计算肯定不大于直接相加之和。假设 loss 的范围在 [0,1] ，N 是 training set 的数据量，可以进一步计算出这一概率。

得到上面的计算结果后，我们知道了，如果要想让 sample 到 bad training set 的概率小，就从两方面调整：

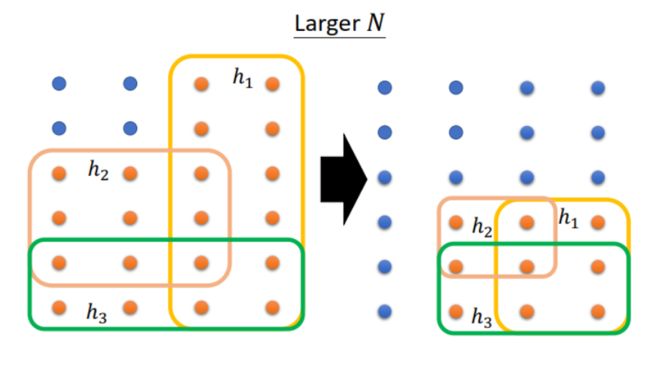
（1）增大 N，也就是增大 training set 的数据量，training set 就越接近 all data，这样 bad $h$ 能影响到的 training set 就少。如下图所示， bad $h$ 的方框面积减小，在总面积的占比减小，因此概率减小。

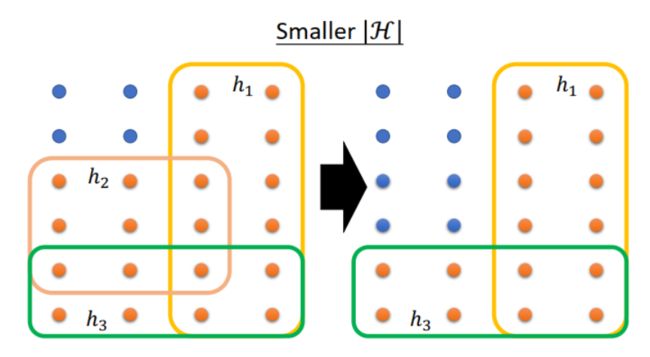
（2）减小 |H|，这样 $h$ 的数目少，bad $h$ 也就少。如下图所示， bad $h$ 的方框个数减少，在总面积的占比减小，因此概率减小。

在实际中，|H| 往往很大，如果 N 小的话，这个概率算出来大于 1，没有意义。例如：|H| =1000，N=100, $ϵ=0.1$, 计算得到 $P(D_{train}isbad)\le 2707$。但是当 N 增大时这个概率就会减小，例如，N 增大到 10000，$P(D_{train}isbad)\le 0.00004$ 。

也可以用于计算所需的 training set 的数据量 N，如下图中的例子所示：

如果能收集到很大量的训练数据，那就好办了。即使用了复杂的模型，|H| 很大，也可以增大 N 来降低 training set 是 bad sample 的概率。

实际中，并不是这么容易收集到大量的数据。很多时候，我们无法决定训练集数据量 N 的大小，只能利用给定的数据。这样看来，就只能调整 |H|，选小一些的 |H|，使 $L(h^{train},D_{all})$ 与 $L(h^{all},D_{all})$ 相差小。但是这样做的话，因为参数集 H 小，可选择的 $h$ 少，可能在 all data 上得到的 $h^{all}$ 并不是最好的，没有达到 all loss 可以达到的最小值。这就是前面提到的 model bias 问题，已经超出了模型的能力范围。

于是，我们陷入两难：

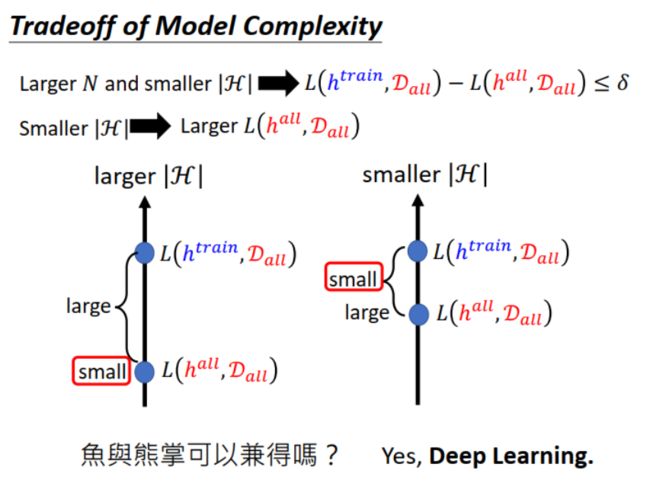
如下图所示，选大一些的 |H|（模型复杂），性能好，$L(h^{all},D_{all})$ 小。但是训练得到的参数 $h^{train}$ 在 all data 上的效果与理想有差距： $L(h^{train},D_{all})$ 与 $L(h^{all},D_{all})$ 相差大。

选小一些的 |H|（模型简单），$L(h^{train},D_{all})$ 与 $L(h^{all},D_{all})$ 相差小。但其实这两个 loss 都大，模型性能并不好。

$L(h^{all},D_{all})$ 小 v.s. $L(h^{train},D_{all})$ 接近 $L(h^{all},D_{all})$ ，看起来只能二选一。怎么办？鱼与熊掌可以兼得吗？

我们可以找一个 H，这个参数集小，可选的 $h$ 少。但是，其中的 $h$ 都是精英啊，可以让 all data 的 loss 小，这样就兼顾两者了。Deep Learning 就是这样的模型。

Why Deep Leaning?

前面在第一课中介绍过，如果只有一层 Hidden Layer，只要神经元的数量足够多，可以表示任意函数，也就是 Shallow network (“Fat” Network)，如下图所示。我们为什么要 Deep network, 而不是 Shallow network?

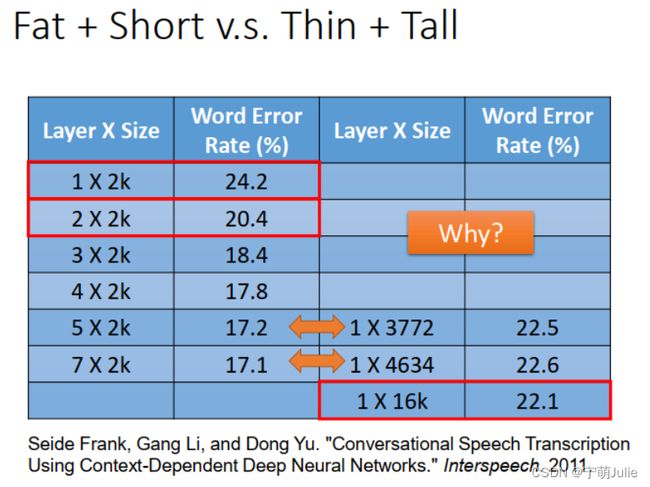
这里有学者做了研究，对比了 Deep Network 与 Shallow Network 在语音识别应用上的性能，结果如下表所示。左边从上至下是 Deep Network 从1层到 7 层的错误率结果。右边是 Shallow Network 的错误率结果，因为它只有一层，依次是神经元数目为 3772，4634，16k 的结果。

表格中：

（1）箭头指示的两组是使用相同数量参数的 Deep Network 和 Shallow Network 的结果。参数量相同时，Deep Network 的错误率明显更低，性能更好。

（2）Deep Network 叠两层时，错误率就降到了 20.4%，比 Shallow Network 最多参数的架构 1x16k 的性能都好。

可见，与 Shallow Network 相比，Deep Network 可以在使用参数量更少的同时，达到更好的模型性能。

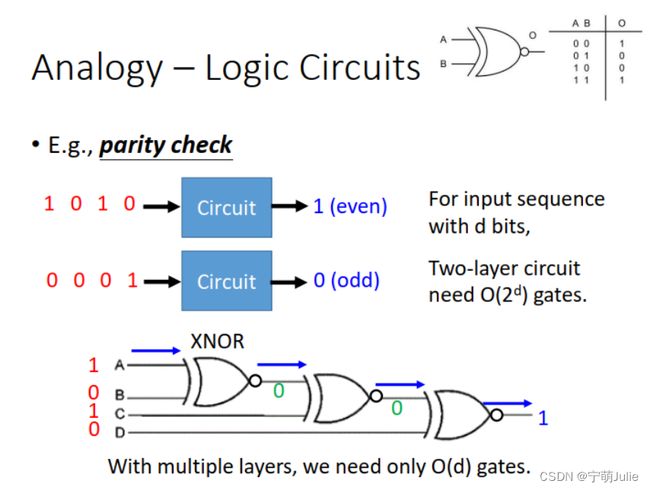
其实不只用在 Deep Learning，很多地方都用到了 Deep Structure 的思想。比如，逻辑电路也是类似的情况。如下图例子所示，实现相同的功能，多层结构比两层结构所需的与非门数量少得多。

再比如，我们在学习编程时都学过“模块化编程”的设计思想。把程序的实现功能分模块，写成函数，这样可以增加复用性，提高开发效率。

还有生活中的例子，剪纸。比如剪窗花，叠成几叠再剪，比在一整张纸上剪要快很多。

我的思考：Deep Network 就是解决一个问题时，首先划分一下有几部分，然后依次完成。感觉和编程算法的 Divide and Conquer 有异曲同工之妙。Shallow Network 就是拿到一个问题就开始解决，又像拿到一本书就从第一页开始看，效率更低。

再来分析 Deep Network:

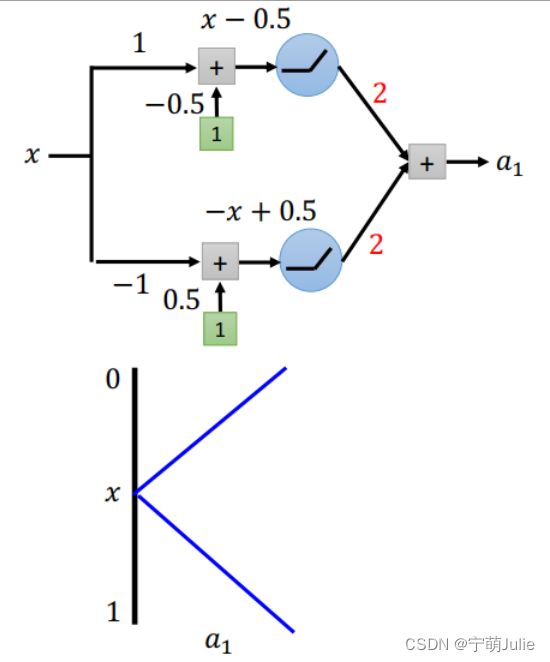
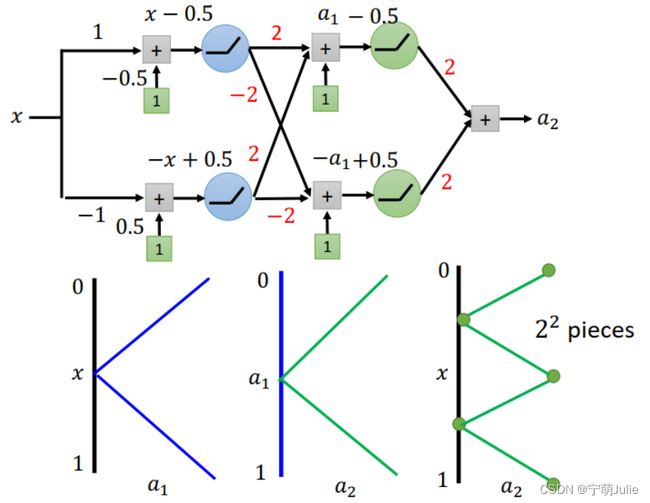
一层结构：两个神经元，激活函数用 ReLU，输出 $a_1$ 与输入 $x$ 的关系如下图所示：

两层结构：如下图所示，第二层 hidden layer 与第一层 hidden layer 的结构相同，因此 $a_2$ 和 $a_1$ 的函数关系与 $a_1$ 和 $x$ 的函数关系相同。这样可以推导出最后输出 $a_2$ 与输入 $x$ 的关系如图中所示：

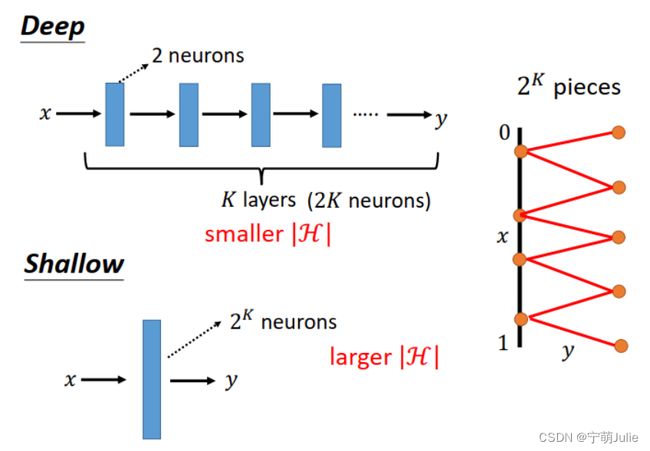
依此类推，假设我们要表示下图所示 $2^K$ 个折线段的函数，使用 Deep Network 需要 K 层，每层 2 个神经元。而使用 Shallow Network 只有 1 层，需要 $2^K$ 个神经元。相比之下，Deep Network 的参数量 |H| 更少。而前面的语音识别的对比测试也显示了，Deep Network 的性能更好。

Deep Network的适用场景：

“Deep networks outperforms shallow ones when the required functions are complex and regular, e.g. Image, speech, etc. have this characteristics.

Deep is exponentially better than shallow even when $y=x^2$.”

Deep Network 适合 function 复杂而有规律的情况。注意，function 指的是模型函数，即要拟合的 $y$ 和 $x$ 的映射函数，不是 loss function。而即使函数是 $y=x^2$ 这样的情况，Deep Network 也远比 Shallow Network 更好。

more about validation set

问题：我用了 validation set，为什么模型还是 overfitting？

上一节课模型训练技巧中介绍了用 validation set 来挑选出合适复杂度的模型，理论上说应该可以避免 model bias 或 overfitting，怎么回事呢？

用 validation set 来选择模型的过程，可以看作是在 validation set 上的“训练”。例如，下图所示有 3 个模型，这样 $|H_{val}|=3$ 。

既然把 validation set 挑选模型的过程看作训练，同样希望 $L(h^{val},D_{all})-L(h^{all},D_{all})\le \delta$，因此希望validation set 是 bad sample 的概率小。从下图所示的公式可知，这就要 $|H_{val}|$ 小或 $N_{val}$ 大。

如果 validation 要选择的模型不多， $|H_{val}|$ 小，这个概率自然小。但是，如果一下子训练过猛，比如从1层结构到 10 层结构都试一遍，每层有 1 到 1000 个神经元可选择，这样下来 $|H_{val}|$ 就有 $1000^{10}$ 之多，此时就很有可能 overfitting。也就是说，如果做 validation 时，待选择的模型太多了，仍然有可能 overfitting。

觉得本文不错的话，请点赞支持一下吧，谢谢！

关注我 宁萌Julie，互相学习，多多交流呀！

参考

李宏毅老师《机器学习 2022》，

课程网站：https://speech.ee.ntu.edu.tw/~hylee/ml/2022-spring.php

视频：https://www.bilibili.com/video/BV1Wv411h7kN