人工智能导论 基础搜索算法

基础搜索算法

在本章中, 我们首先会对 推断 这一逻辑过程进行建模, 并将其含义与 搜索 整合起来, 解释 将推断的逻辑行为建模和实现为搜索算法 的原理与合理性.

其次, 我们将介绍包括深度优先搜索 (DFS) 在内的数种基础搜索算法.

1. 推断和搜索

下面介绍两种对问题的建模思路: 将问题建模为 状态转换问题 和 将问题建模为 逻辑推断问题.

1.1 将问题建模为状态转换问题

考虑如下的一个问题:

给定如上图所示的初始条件, 我们需要生成一系列由 Dalek 所执行的操作组成的策略, 从而使得书架被运到客厅 (sitting room), 且 Dalek 最终位于大厅 (hall) 内.

我们可以如下分别表达这个问题所描述的两种事实:

// Fluents
[in(dalek, hall), 
 in(bookcase, hall), 
 in(table, study)]

// Permanents
[adjacent(bedroom, hall)
 adjacent(hall, sitting-room), 
 adjacent(sitting-room, study)]

并且我们可以将问题的目标描述如下:

// Goals
[in(dalek, hall), in(table, sitting-room)]

注意在这里我们使用数组存储可变事实, 既定事实和目标.

我们首先对 推断 这一逻辑操作进行行为上的拆解. 任何推断都必须存在一个被推断主体, 也就是问题本身, 因此要对推断建模, 我们首先需要对问题本身进行建模.

进一步地, 问题的本质是: 我们需要生成一个符合某些限制条件的策略, 使得问题中所提出的要求可以通过执行策略来满足. 显然地, 任何一个问题又可细分为四个部分:

1. 当前已知, 但会随着我们采取行为而被改变的可变事实 (Fluents).
2. 当前已知, 且永不会被改变的既定事实 (Permanents).
3. 问题所提出的目标 (Goal).
4. 策略的组成部分: 我们可以执行的所有行为 (Actions).

我们下面限定 Dalek 的行为:

// Actions
carry(bookcase, study, sitting-room), 
go(sitting-room, hall)

显然更进一步地, 任何行为又包含四个部分:

1. 我们具体要执行的操作.
2. 该行为能够被执行所需要满足的前提条件.
3. 在行为执行后, 所出现的新事实.
4. 在行为执行后, 所消失的旧事实.

我们可以进一步地细化两个行为:

// carry
action-type(
    carry(Object, Room1, Room2),
    pre-conds([in(Object, Room1), 
               in(dalek, Room1), 
               adjacent(Room1, Room2)]),
    add-list([in(dalek, Room2), in(Object, Room2)]), 
    del-list([in(dalek, Room1), in(Object, Room1)]).
)

// go
action-type(
    go(Room1, Room2), 
    pre-conds([in(dalek, Room1), 
               adjacent(Room1, Room2)]),
    add-list([in(dalek, Room2)]), 
    del-list([in(dalek, Room1)]).
)

而通过将细化的行为描述中所有的变量赋值, 我们就可以将其 实例化.

我们可以将所有可能采取的行策略 表示为一个多叉树 , 其中: 节点由一个表示当前状态的可变事实列表代表, 而每一条边都是一个 被实例化的 行为.

每个节点对应的子树数量为在该节点上可采取的行为的种数, 而每层节点的数量为上一整层节点在进行所有可能的行为后所能被变换到的新状态的数量总和.

在完成对问题的建模后, 我们还需要对应的逻辑方法用于解决问题并给出可行解. 由于我们将问题的状态转换建模为树, 我们相应地就需要一套用来在树中搜索可行路径 (在解空间内搜索可行解) 的方法.

称程序用于在所有可能的推断中选择用于解决问题达成目标的特定推断的算法为 启发算法 (Heuristics).

1.2 将问题建模为逻辑推断问题

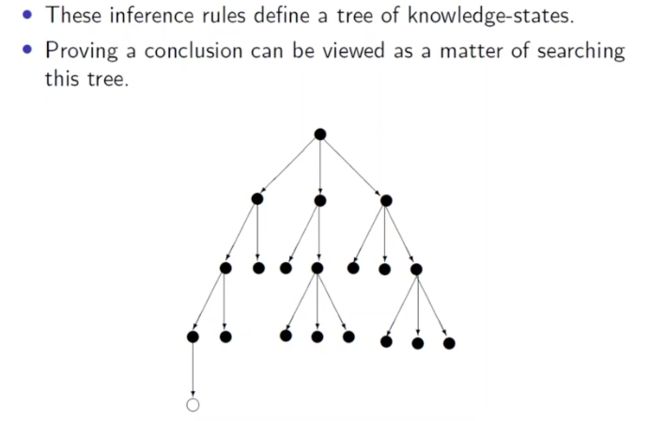
我们除了将求解问题的过程视为状态转换过程外, 还可以将其抽象为逻辑推断问题. 在这一建模思想下, 解决问题的核心是下图所示的逻辑推断规则:

显然, 在开始解决问题时我们有一系列的 已知事实. 通过应用不同的推断规则, 已知事实就会发生不同的变化: 我们可能从已知的一些事实中推断出新的.

由此, 从初始状态下的已知事实出发, 执行所有可能被应用的逻辑推断规则的过程就可同样地被建模成 知识状态树:

通过逐步地确定在不同的状态下基于当前的知识应该应用哪条三段论推理规则最终使知识状态 (Knowledge State) 和目标状态保持一致, 我们也可以求得问题的解. 在这一建模思想下, 求解问题的过程也就是在知识状态树上搜索的过程.

2. 搜索算法

从上一节中可以看出, 从对现实问题的两种建模方式出发, 解决问题的本质最终都殊途同归地表示为了 在某种状态树上的搜索过程. 因此, 在本节中, 我们介绍四种基础的搜索算法.

2.1 深度优先搜索 DFS

深度优先搜索的原理是, 搜索到某个节点后, 若它不为所需要的节点, 则下一步总是以搜索它的子节点而非同级节点为最高优先. 该原理决定了其行为是: 一条条地纵向遍历, 从上到下地 完整 搜索每一条可行路径, 直到得到一个可行路径 (可行解) 为止. 其伪代码如下:

dfs(Queue):
    if Queue is non-empty:
        FirstNode := Queue.pop()
        if FirstNode is goal_node:
            return FirstNode
        add_daughters_of_FirstNode_to_the_front_of_the_queue
        return dfs(Queue)
    return failure

我们也可以这样递归地实现 DFS:

dfs(Node):
    if Node is goal_node:
        return Node
    for each Daughter in daughters_of_Node:
        if dfs(Daughter) != failure:
            return dfs(Daughter)
    return failure

2.2 广度优先搜索 BFS

广度优先的原理是, 搜索到某个节点时, 若它不为所需要的节点, 则下一步总是以搜索与其同级的节点而非其子节点为最高优先. 故其行为是: 一级级地横向遍历, 从左到右地 完整 搜索每一级上的全部节点, 直到得到一个可行路径 (可行解) 为止. 其伪代码如下:

bfs(Queue):
    if Queue is non-empty:
        FirstNode := Queue.pop()
        if FirstNode is goal_node:
            return FirstNode
        add_daughters_of_FirstNode_to_the_end_of_the_queue
        return bfs(Queue)
    return failure

深度优先和广度优先搜索仍然属于结构最为简易的搜索方法, 它们给出的解可能并非解空间中的最优解.

为了分别解与解之间的优劣, 我们引入 代价 的概念, 它刻画了一个人为定义的, 反映实际情况中为了实现某个解所需要付出的成本的大小. 为了找到 成本最低 的解, 我们进行如下假设:

1. 假定我们可能采取的任何行为都有一个 (!非负的) 成本 (Cost). 因此, 每个节点 $\nu$ 对应地有一个数据 $C(\nu )$ 表示从根节点执行一系列行为后到达该点所需要付出的成本 Cost so-far.

2. 假设对任何问题而言, 为了实现目标所需要付出的代价都是有限的, 因此存在一个非负的 成本下界 (lower bound). 结合假设 1, 我们可知每个节点 $\nu$ 都有一个对应的 从该状态转移到问题可满足状态所需要付出的代价的最小估计 $U(\nu )$.

需要注意: 深度优先和广度优先搜索伪代码除了可以表示为上文提到的 栈实现 外, 还可表示为 (实际上最常用到的) 递归实现, 递归实现在实际程序执行时生成的内部栈和栈实现是完全一致的, 二者实际上等价.

我们下面介绍两种可用于求解成本最低解的算法: 分支定界算法 (branch-and-bound) 和 A*:

2.3 分支定界算法 Branch and Bound

我们定义总代价 $K(\nu )$:

$$K(\nu ):=C(\nu )+U(\nu )$$

根据上述分析, 此式显然成立. 在算法执行之初, $K(\nu )$ 是未知的. 当算法找到第一个解时, 其代价 $C(\nu )$ 被自然地赋值为 $K(\nu )$, 因为 $U(\nu )=0$, 此式我们记录下该解并对 $K(\nu )$ 赋值. 随着算法继续执行搜索, 我们可能找到更多的解. 若某个解的 $K(\mu )⩽K(\nu )$, 我们更新最优解和相应的 $K(\nu )$. 在确定筛选完了所有解后, 此时的 $\nu$ 就是所需的最优解.

在实际的分支定界算法中, 为了提高算法效率我们还会对搜索树进行剪枝.

分支定界算法始终围绕状态树进行. 将原问题视为根节点并从这里出发, 搜索行为类似于深度优先搜索. 分支的含义就是将大的问题分割成小的问题. 大问题可以看成是搜索树的父节点, 故从大问题分割出来的小问题就是子节点, 分支就是不断增加子节点的过程.

定界指在分支的过程中检查子问题的成本上下界. 若子问题不能产生更优解, 则对这一支执行剪枝. 直到所有子问题都不能产生一个更优的解时, 算法结束.

分支定界算法的伪代码如下:

# BestCost变量维护当前已知最优解的最低代价

BestCost = INFINITY     # 初始化已知最低代价
CurrentBest = none      # 初始化当前最优解

bnb(Queue, BestCost):
    if Queue is non-empty:
        # 逐个检查序列中的所有节点
        FirstNode := Queue.pop()    
        
        # 只考虑成本上界低于当前最低代价的节点
        if K(FirstNode) < BestCost:

            # 若某个节点是目标节点且达到该节点所需代价更少
            # 则更新当前最优解和已知最小代价
            if K(FirstNode) is_a_goal_node:
                CurrentBest := FirstNode
                BestCost := K(Currentbest)
            
            # 反之检索该节点下的所有子节点
            else
                add_daughters_of_FirstNode_to_the_front_of_Queue

        # 递归检索序列中的每个节点        
        bnb(Queue, BestCost)
    
    # 检索完序列中所有节点后若最低代价被更新了则返回当前已知最优解
    else if BestCost != INFINITY:
        return CurrentBest

    # 否则说明无解
    return failure

2.4 A* 算法

在上学期的 Java Coursework 中, 我们已经部分地了解了 A* 算法. 在此处我们将介绍的 A* 算法的具体特征与之有所不同. 我们首先定义 A* 算法:

广义上的 A* 算法具备有两个部分组成的损失计算函数:

1. 从初始节点到当前节点所需要付出的代价.
2. 从当前节点到目标节点所需要付出的代价.

我们的目标为计算出总成本最小的解. 要实现这一目标, 我们可以通过优先选择在每一步中成本 $C(\nu )$ 最小的节点 $\nu$, 也就是 优先选择局部最优.

A* 算法的伪代码如下:

# 定义: K(v) = C(v) + U(v)
# v为某个节点, C(v) 为到这个节点所已经花的代价
# U(v) 为从这个节点到目标节点还要花费的预估代价

ast(Queue):
    if Queue is non-empty:
        FirstNode := Queue.pop()
        if FirstNode == GoalNode:
            return FirstNode
        compute daughters of FirstNode, then add to Queue
        
        # 该步非常关键, 决定了A*算法只会
        # 优先考虑预估成本最小的节点
        order Queue by K    
        
        return ast(Queue)
    return failure