逻辑回归(logistics regression)简单理解

逻辑回归(logistics regression)简单理解

    本文用简单有趣的例子对逻辑回归进行讲解，主要目的是为了更快、更容易的理解逻辑回归的基本原理，并能够独立的进行简单的运用。

  首先，需要知道的是，逻辑回归用于分类！

  下面，我们来看一个小例子。现在有一堆硬币，其中有一部分是假的，另外全是都真的。然后，你可以将“逻辑回归”当作一个特殊的人，只要你告诉他该如何分类，那么他就可以快速的将这堆硬币的真假给分开，但是，你告诉他的方法越好，他分正确的比例也一般越高。
  那么，怎么告诉（训练）他呢？比如，你可告诉他，称硬币的重量啊，一般假的硬币重量比较轻，但是如果他学会了这种区分方法，他还是可能分错。这个时候，你可以再综合一种区分方法，比如一般假硬币的光泽没有真硬币的好，他分正确的几率很可能会有所提高，当然，可能你将综合了这两种的区分方法都告诉他，他还是会分错一小部分。
  刚才的故事讲完了，现在我们来说一下，这个小例子和逻辑回归到底有什么关系？
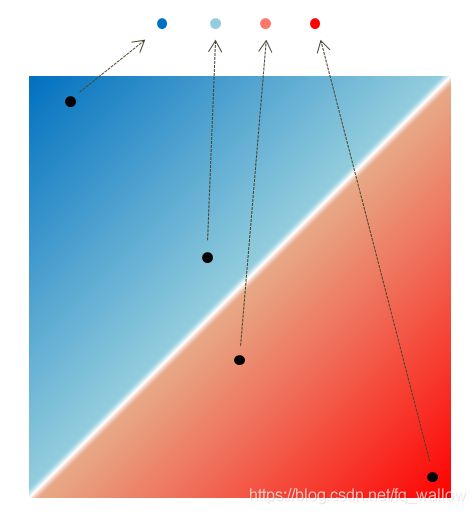
  我们先偷偷开启一下上帝视角，用一个图来看一下。其中，绿色的圈圈表示真硬币，红色的圈圈表示假硬币。

  然后，我们把上帝视角关一下。
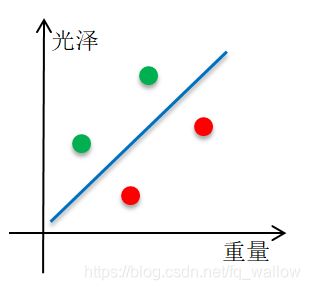
  接下来，我们先来看真假硬币重量的分布情况，这里只看重量这一个属性。

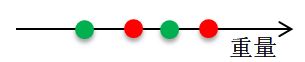
  接下来，我们先来看真假硬币光泽的分布情况，这里只看光泽这一个属性。

  通过上面两个图，我们发现，只告诉他怎么用重量来区分，或只告诉他怎么用色泽来区分，很明显会出现一下错误。
  那么，接下来，我们综合两种属性来帮助他学习（训练）。可是，在学习的时候，他觉得这3条曲线都可以用来区分，但是不知到哪条比较好，然后为什么好呢？

  根据我们的直觉，这3条线中蓝色的线用来区分比较好，可是我们需要有一个合理的解释！暂且就认为所有的点到该分界线距离的平方和越小越好，这个解释好像有些合理。
  那么，如果现在训练数据再增加一个（假设距离分界线很远），如下图所示

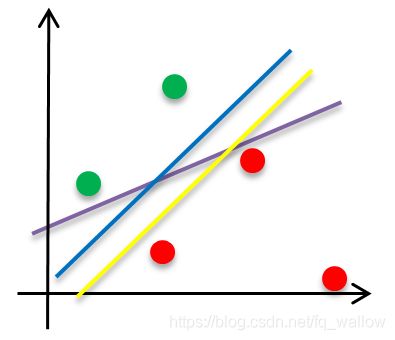
  我们可能还是觉得用蓝色的线进行区分比较好，但用黄色的线当作分界线来计算所有点到分界线的距离的平方和，反而可能更小一些。（画的可能不标准，但真有可能）
  于是，我们刚才的解释好像不太适用。综合刚才的经验，我们给定两个假设：
   1. 距离分界线越远的点越是能确定它属于哪一类。（当某一点在分界线上时，属于两类的可能性相等）
   2. 距离分界线越远的点，对分界线的确定，影响越小。（也就是说，这条分界线主要依靠其附近的一些点来确定）
  显然，当有个点距离分界线很远（如刚才那个红色的点），我们在学习规则的时候几乎不用考虑它，在计算的时候给予它的权重也就很小。
  再回顾一下我们的目标：给一部分已经标识了真假的硬币用来训练，剩下的硬币用学习到的规则进行分类。（这篇文章中暂时只考虑两个属性，实际运用时，可考虑多种属性，可能效果更好）
  根据我们刚才确定的假设以及目标，我们可以将真硬币当作‘1’，假硬币当作‘0’，然后大致可以画出下面的函数用来分类

  解释一下上图的含义，横坐标表示某个点与分界线的距离，纵坐标表示该点属于‘0类’或属于‘1类’的程度。显然当点与分界线距离为0的时候，我们很难判断它属于哪一类，此时它属于两类的可能性相等，在图中用（0，0.5）来表示。
  下面，我们举个例子，如下图所示，判断一下红黄蓝3个点分别属于哪一类，哪个点距离分界线最近，哪个点距离分界线最远，哪个点属于某一类判断的比较准确？

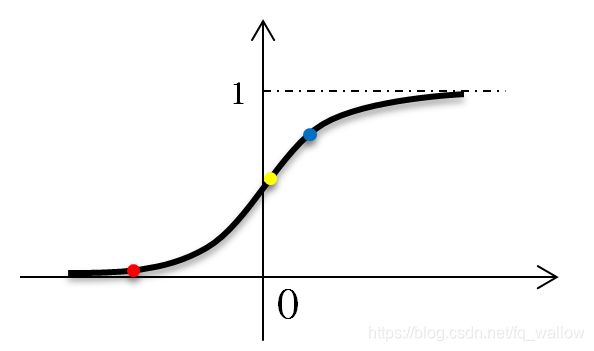
  答：红色的点属于‘0类’，黄色和蓝色的点属于‘1类’，黄色的点距离分界线最近，红色的点距离分界线最远，判断红色的点属于‘0类’的准确性比判断另外两个点属于‘1类’的准确性要高。（只是准确性更高）
  了解了上面的例子，我们来找与这个图像类似的函数，我们发现sigmod函数与之很像（不一定非要用这个函数），我们接下来就使用这个函数来学习规则。
  先来了解一下sigmod函数的部分性质。
  sigmod函数图像如下：

  由于我们刚才设定的x轴表示某点到分界线的距离，所以需要在sigmod函数f（x）的基础上进行变换，现在设定g（x）表示点x到分界线的距离，那么，新的分类函数则可以写成：

  我们发现分类函数F(x)中的g（x）还没确定，要确定函数g(x)，首先得知道分界线，现在假设分界线为：

  其中

  则假设的线性分界线可简化为

  下面我们再来计算一下点x到直线距离的函数g(x)（注意：现在的x比原始数据多了一项，因为在最前面增加了一项x0 = 1，这么做的目的只是为了使最后的式子看起来更简洁）

  我们发现如果知道了线性分类函数，则g(x)函数中，那个w二范数是一个常数，如果将其去掉，不仅能极大的简便计算，还能保证任意两点到分界线的相对距离保持不变。还有，我们最开始所说的距离，并不都是正的距离，还有负的距离，所以需要将绝对值给去掉。（注意：绝对值肯定需要去掉，因为需要正和负的距离，但下面w-的二范数可以不用省略掉，不过省略掉可以简化计算）
  则点到直线的距离也可表示为：

  那么新的分类函数完整形态为：

  含有未知参数w的分类函数我们写出来了，现在我们还需要考虑怎么通过已知的训练数据将未知参数w给学习好，也就是需要学习线性分类的函数。
  再看一下最开始的那个有好几条分界线的图

  现在需要解释一下，为什么蓝色的分界线比较好？
  我们先选择紫色的分界线，然后将点画在刚才学习的分类函数上，大致情况如下图所示

  结合横纵坐标的意义，相信可以理解这个图的含义，下面分别以黄色和蓝色的线为分界线画分类函数的图

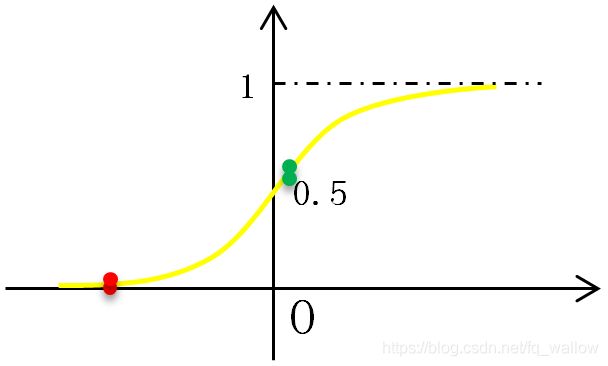
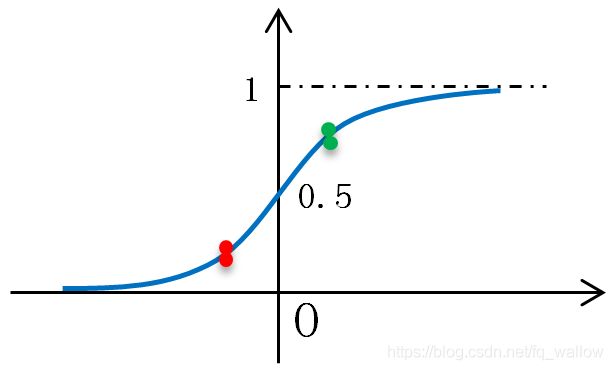
  我们发现，每一个点都有属于某一类都有一个概率，有的高有的低，任意一个点属于‘1类’的概率就是它纵坐标的值，类似的，任意一个点属于‘0类’的概率就是用1减去它纵坐标的值。然后我们去判断某一点到底属于哪一类，就选择属于哪类概率最大的。
  以蓝色的线作为分界线，好像能够使所有点更加‘均衡’。
  通过大概的计算，我们也发现以蓝色的线作为分界线，能够使得所有点属于某类的整体概率最大。（即计算所有点属于某类的概率，然后将这些概率相乘）
  那么我们再增加一个假设：能够使得整体正确概率越大的分界线越好。假设现在有训练数据d1 , d2 , … , dn，其类别分别为l1 , l2 , … , ln，根据刚才的假设，则求最佳分界线的参数，可以用公式描述为

  其中，Fi(w)表示第i个数据以w为参数的分界线的分类概率。
  为了简化计算，可等价为

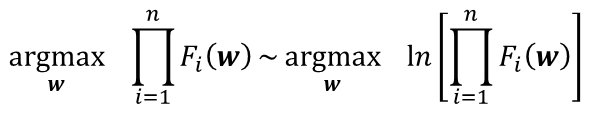
  看到这个式子，很显然可以利用最大似然估计进行求解。这里直接给出结果，最大似然估计如何计算可参看
  最大似然估计链接（参看第二节）

  做到这一步，考虑一个问题，为什么不能像之前求最大似然估计那样对每个参数求偏导等于0，然后直接求出最优解？
  答：对所有wi(i = 1 , 2 , … , n)求偏导，令其都等于0，最后虽然可以组成一个n元其次方程组（但非线性），理论上也可以求解，但在比较复杂的问题中，一般无法求解。所以一般采用梯度下降法进行求解。
  接下来，我们采用梯度下降法对下面这个式子进行求解（本文不讲解梯度下降法，直接运用）

  为了简化，令

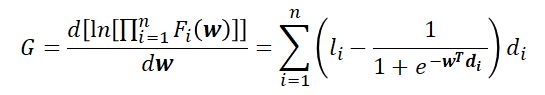
  利用梯度下降求解该问题算法过程如下：

  最后输出的w即是在之前那些假设的前提下，得到的最好的分界线的参数。如果没有那些假设，它就不一定是最好的。
  好，读到此处，逻辑回归的讲解就基本结束了，然后我简单的说一下我的感想：写这篇博客，我并没有按照我自己学习的那样去写，也没有说太多的专有名词（如损失函数），因为主要目的是为了让你更好理解，而不是仅仅会公式推导。我由浅入深的，基本每一步都说明了为什么，引导你去思考，也想让你学会思考，然后慢慢成长，有一些步骤，我在网上查不到原因，于是我就按照自己的想法去解释，如果你发现了什么错误，可以跟我说一声。
  最后，用下面这个图来总结一下我理解的逻辑回归，这次我就不解释了，希望，你能独立的看懂。