机器学习入门(五):线性回归—从模型函数到目标函数
从数据反推公式
假设我们获得了这样一张表格,上面列举了美国纽约若干程序员职位的年薪:
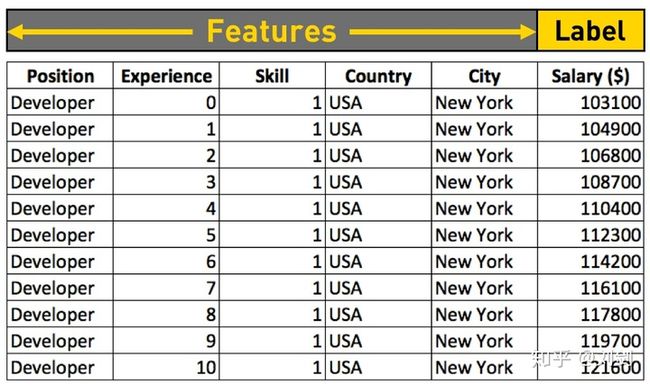
大家可以看到,表格中列举了职位、经验、技能、国家和城市几项特征。除了经验一项,其他都是一样的。不同的经验(工作年限),薪水不同。而且看起来,工作年头越多,工资也就越高。
那么我们把 Experience 与 Salary 抽取出来,用 x 和 y 来分别指代它们。

它们是不是成正比的呢?y 与 x 没有比例关系,y 直接除以 x 肯定不行。
那么,是不是有可能是 y = a + bx 这样的线性相关关系呢?
我们可以先在二维坐标系里通过画图来看一下 x 与 y 的关系:

当我们用6个点在坐标系里标注出工作年限从0到5的工资收入后,发现:把这6个点连起来,基本上就成了一条直线。那么假设存在 y = a + bx,是合理的。
既然是条直线,又有现成的 x = 0 的情况 103100 = a + b * 0,我们可以直接得出 a = 103100,带入 104900 = 103100 + b 得出 b =1800。
将 a 和 b 的值带入 x = 2、3、4、5 几项,发现结果与真实值都不完全一样,但真实值和预测值差别不大,只有1%~2%的差距。
那么我们将 x = 6 带入 y = 103100 + 1800 * x,得出 y = 113900,虽然和实际的114200并不完全一样,但差距也不到3%。
综合利用训练数据,拟合线性回归函数

上面获得 a、b 两个参数取值的方法很直接,不过并不具备通用性,原因在于:
- 不是所有的数据都会提供 x = 0 的情况,让我们直接得到 a 的取值;
- 获取 a 和 b 各自只用到一个数据,这样做带有很大的偶然性,不仅浪费了多个数据综合求取参数的机会,而且,很可能无法得到真正合理的结果。
既然我们认为 x 和 y 满足线性相关关系,那么线性函数: y = a + bx,就是我们的模型函数。其中 y 也可以用 f(x) 来表示。
我们要做的是综合利用所有的训练数据(工作年限从0-5的部分)求出 y = a + bx 中常数 a 和 b 的值。
线性回归的目标函数
综合利用的原则是什么呢?就是我们要求的这个 a 和 b,在将训练样本的 x 逐个带入后,得出的预测年薪 y’ = a + bx 与真实年薪 y 整体的差异最小。
具体的一个样本的 y 和 y’ 的差异用 (y′−y)2 来表示。
怎么衡量这个整体差距呢?我们用下面这个公式,我们把它叫做为 Cost Function,形式如下(其中 m 为样本的个数,在本例中 m 取值为6):
J(a,b)=12m∑mi=1(y′(i)−y(i))2=12m∑mi=1(a+bx(i)−y(i))2
在 y = a + bx 这个模型函数中,a 和 b 是常量参数,x 是自变量,而 y 是因变量。
但到了 J(a,b) 中,x(i) 和 y(i) 是常量参数(也就是 m 个样本各自的 x 和 y 值),而 a 和 b 成了自变量,J(a,b) 是因变量。能够让因变量 J(a, b) 取值最小的自变量 a 和 b,就是最好的 a 和 b。
我们要做的,就是找到最好的 a 和 b。
但是,在讲求解 a,b 之前,我们先要特别强调一个概念——线性。
线性=直线?
线性概念的混淆
为什么要说线性呢?
因为,很多人简单认为“线性回归模型假设输入数据和预测结果遵循一条直线的关系”。
确实,从上面那个例子来看,x 和 y 的关系的确是拟合成了一条直线(参见下图):
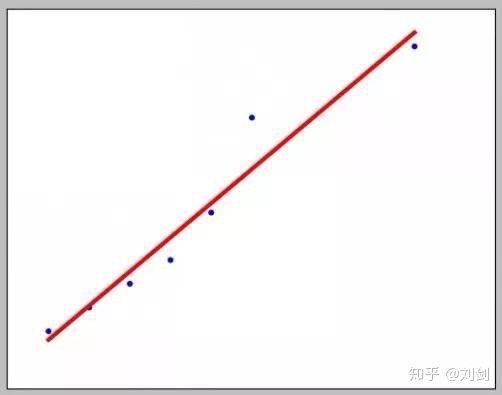
而且,在上例中,我们最开始的假设是 y = a + bx ——大家回顾一下初中数学,在我们刚学坐标系的时候,最早学的就是如何在直角坐标系里构造一条直线:y = a + bx。
所以,难怪会有同学把线性回归理解成自变量(特征 x)和因变量(结果 y)的关系是一条直线。
但是,这种理解是一叶障目。
线性的含义
线性回归模型是:利用线性函数对一个或多个自变量 (x 或 (x1,x2,...xk))和因变量(y)之间的关系进行拟合的模型。
也就是说,线性回归模型构建成功后,这个模型表现为线性函数的形式。
线性函数的定义是:一阶(或更低阶)多项式,或零多项式。
当线性函数只有一个自变量时,y = f(x)。
f(x) 的函数形式是:
f(x) = a + bx (a、b 为常数,且 b≠0)—— 一阶多项式
或者 f(x) = c (c 为常数,且 c≠0) —— 零阶多项式
或者 f(x) = 0 —— 零多项式
但如果有多个独立自变量,y=f(x1,x2,...,xk) 的函数形式则是:
f(x1,x2,...,xk)=a+b1x1+b2x2+...+bkxk
也就是说,只有当训练数据集的特征是一维的时候,线性回归模型可以在直角坐标系中展示,其形式是一条直线。
换言之,直角坐标系中,除了平行于 y 轴的那些直线之外,所有的直线都可以对应一个一维特征(自变量)的线性回归模型(一元多项式函数)。
但如果样本特征本身是多维的,则最终的线性模型函数是一个多维空间内的[一阶|零阶|零]多项式。
总结一下:特征是一维的,线性模型在二维空间构成一条直线;特征是二维的,线性模型在三维空间中构成一个平面;若特征是三维的,则最终模型在四维空间中构成一个体,以此类推。
用线性回归模型拟合非线性关系
在输入特征只有一个的情况下,是不是只能在二维空间拟合直线呢?其实也不一定。
线性模型并非完全不可能拟合自变量和因变量之间的非线性关系——听着有点矛盾啊,其实这是一个操作问题。
比如,有一些样本,只有一个特征,我们把特征和结果作图以后发现,是这个样子的:

这些样本特征和结果关系的走势,根本不是直线嘛。看起来还挺像二阶曲线的。
这个时候,我们完全可以把特征从一个“变成”两个:
设 X=(x1,x2)(其中 x1=x2;x2=x),有:
f(x1,x2)=a+b1x2+b2x=a+b1x1+b2x2
这就相当于拟合了一条二阶多项式对应的曲线。
再设 B=(b1,b2),则:
f(X)=a+BX
这样一来,我们只需要在二维向量空间里训练 f(X)=a+BX,就可以了。
当然,这种操作也不限于在一维到二维之间的转换,一维也可以转为三维、四维、n 维;或者原本的 k 维也可以每一维都求平方后作为新特征引入,转为 2k 维,如此种种……依需要而取就好。