4. 卷积神经网络CNN
文章目录
- 4. 卷积神经网络CNN
-
- 4.1 概念
-
- 4.1.1 概念
- 4.1.2 用途
- 4.2 结构介绍
-
- 4.2.1 结构简介
- 4.2.2 卷积层
-
- 1) 基本概念
- 2) 前期准备
- 3) 参数共享
- 4) 卷积运算
-
- a) 二维卷积运算
- b) 偏置
- c) 填充
- d) 三维卷积运算
- 5) 小结
- 4.2.3 池化层
-
- 1) 基本概念
- 2) 小结
- 4.2.4 全连接层
-
- 1) 基本概念
- 2) 例子
- 4.2.5 激活函数RelU
- 4.2.6 小结
- 4.2.7 各种计算公式
-
-
- 1) 卷积计算公式
- 2) 膨胀卷积计算公式
- 3) 池化计算公式
- 4) 转置卷积公式
-
- 4.3 典型CNN
-
- 4.3.1 LeNet
-
- 1) 基本概念
- 2) 网络结构
- 3) 特点
- 4.3.2 AlexNet
-
- 1) 基本概念
- 2) 网络结构
- 3) 网络特点
- 4.3.3 VGGNet
-
- 1) 基本概念
- 2) 网络结构
- 3) 网络特点
- 4.3.4 ResNet
-
- 1) 基本概念
- 2) 网络结构
- 3) 网络特点
4. 卷积神经网络CNN
文章链接
https://gitee.com/fakerlove/deep-learning
以算法区分深度学习应用,算法类别可分成三大类:
- 常用于影像数据进行分析处理的卷积神经网络(简称CNN)
- 文本分析或自然语言处理的递归神经网络(简称RNN)
- 常用于数据生成或非监督式学习应用的生成对抗网络(简称GAN)
资料参考
https://www.zybuluo.com/hanbingtao/note/485480
参考资料2
https://www.cnblogs.com/wj-1314/p/9754072.html
4.1 概念
4.1.1 概念
参考资料
https://blog.csdn.net/qq_25762497/article/details/51052861
卷积神经网络是近年发展起来的,并引起广泛重视的一种高效识别方法,20世纪60年代,Hubel和Wiesel在研究猫脑皮层中用于局部敏感和方向选择的神经元时发现其独特的网络结构可以有效地降低反馈神经网络的复杂性,继而提出了卷积神经网络(Convolutional Neural Networks-简称CNN)。
现在,CNN已经成为众多科学领域的研究热点之一,特别是在模式分类领域,由于该网络避免了对图像的复杂前期预处理,可以直接输入原始图像,因而得到了更为广泛的应用。 K.Fukushima在1980年提出的新识别机是卷积神经网络的第一个实现网络。随后,更多的科研工作者对该网络进行了改进。其中,具有代表性的研究成果是Alexander和Taylor提出的“改进认知机”,该方法综合了各种改进方法的优点并避免了耗时的误差反向传播。
所以哪里不同呢?卷积神经网络默认输入是图像,可以让我们把特定的性质编码入网络结构,使是我们的前馈函数更加有效率,并减少了大量参数。
具有三维体积的神经元(3D volumes of neurons)
卷积神经网络利用输入是图片的特点,把神经元设计成三个维度 : width, height, depth(注意这个depth不是神经网络的深度,而是用来描述神经元的) 。比如输入的图片大小是 32 × 32 × 3 (rgb),那么输入神经元就也具有 32×32×3 的维度。
传统神经网络
卷积神经网络
一个卷积神经网络由很多层组成,它们的输入是三维的,输出也是三维的,有的层有参数,有的层不需要参数。
4.1.2 用途
1、图像分类 (Classification)
顾名思义就是将图像进行类别筛选,通过深度学习方法识别图片属于哪种分类类别,其主要重点在于一张图像只包含一种分类类别,即使该影像内容可能有多个目标,所以单纯图像分类的应用并不普遍。不过由于单一目标识别对深度学习算法来说是正确率最高的,所以实际上很多应用会先通过目标检测方法找到该目标,再缩小撷取影像范围进行图像分类。所以只要是目标检测可应用的范围,通常也会使用图像分类方法。
图像分类也是众多用来测试算法基准的方法之一,常使用由ImageNet举办的大规模视觉识别挑战赛(ILSVRC)中提供的公开图像数据进行算法测试。图像分类属于CNN的基础,其相关算法也是最易于理解,故初学者应该都先以图像分类做为跨入深度学习分析的起步。使用图像分类进行识别,通常输入为一张图像,而输出为一个文字类别。
2、目标检测 (Object Detection)
一张图像内可有一或多个目标物,目标物也可以是属于不同类别。算法主要能达到两种目的:找到目标坐标及识别目标类别。简单来说,就是除了需要知道目标是什么,还需要知道它在哪个位置。
目标检测应用非常普遍,包含文章开头提到的人脸识别相关技术结合应用,或是制造业方面的瑕疵检测,甚至医院用于X光、超音波进行特定身体部位的病况检测等。目标识别的基础可想象为在图像分类上增加标示位置的功能,故学习上也不离图像分类的基础。不过目标检测所标示的坐标通常为矩形或方形,仅知道目标所在位置,并无法针对目标的边缘进行描绘,所以常用见的应用通常会以「知道目标位置即可」作为目标。
最常见的算法为YOLO及R-CNN。其中YOLO因算法特性具有较快的识别速度,目前已来到v3版本。R-CNN针对目标位置搜寻及辨识算法和YOLO稍有不同,虽然速度稍较YOLO慢,但正确率稍高于YOLO。使用目标检测进行识别,通常输入为一张图像,而输出为一个或数个文字类别和一组或多组坐标。
3、语义分割 (Semantic Segmentation)
算法会针对一张图像中的每个像素进行识别,也就是说不同于目标检测,语义分割可以正确区别各目标的边界像素,简单来说,语义分割就是像素级别的图像分类,针对每个像素进行分类。当然这类应用的模型就会需要较强大的GPU和花较多时间进行训练。
常见应用类似目标检测,但会使用在对于图像识别有较高精细度,如需要描绘出目标边界的应用。例如制造业上的瑕疵检测,针对不规则形状的大小瑕疵,都可以正确描绘。医学上常用于分辨病理切片上的病变细胞,或是透过MRI、X光或超音波描绘出病变的区块及类别。算法如U-Net或是Mask R-CNN都是常见的实作方法。使用语义分割进行识别,通常输入为一张图像,而输出也为一张等大小的图像,但图像中会以不同色调描绘不同类别的像素。
4.2 结构介绍
资料参考
https://blog.csdn.net/qq_25762497/article/details/51052861
4.2.1 结构简介
- 卷积层(Convolutional layer),卷积神经网路中每层卷积层由若干卷积单元组成,每个卷积单元的参数都是通过反向传播算法优化得到的。卷积运算的目的是提取输入的不同特征,第一层卷积层可能只能提取一些低级的特征如边缘、线条和角等层级,更多层的网络能从低级特征中迭代提取更复杂的特征。
- 线性整流层(Rectified Linear Units layer, ReLU layer),这一层神经的活性化函数(Activation function)使用线性整流(Rectified Linear Units, ReLU)。
- 池化层(Pooling layer),通常在卷积层之后会得到维度很大的特征,将特征切成几个区域,取其最大值或平均值,得到新的、维度较小的特征。
- 全连接层( Fully-Connected layer), 把所有局部特征结合变成全局特征,用来计算最后每一类的得分。
4.2.2 卷积层
1) 基本概念
问题的出现???
普通神经网络把输入层和隐含层进行“全连接(Full Connected)“的设计。从计算的角度来讲,相对较小的图像从整幅图像中计算特征是可行的。
但是,如果是更大的图像(如$96\times 96 $的图像),要通过这种全联通网络的这种方法来学习整幅图像上的特征,从计算角度而言,将变得非常耗时。
你需要设计 1 0 4 ( = 10000 ) 10^4(=10000) 104(=10000)个输入单元,假设你要学习 100 个特征,那么就有 1 0 6 10^6 106个参数需要去学习。与$ 28\times 28 $的小块图像相比较, $96\times 96 $的图像使用前向输送或者后向传导的计算方式,计算过程也会慢 100 100 100倍。
-
输入特征图
卷积层的输入数据
-
输出特征图
卷积层输出数据
-
感受野
每个隐含单元连接的输入区域大小叫r神经元的感受野(receptive field)。
-
过滤器
由于卷积层的神经元也是三维的,所以也具有深度。卷积层的参数包含一系列过滤器(filter),每个过滤器训练一个深度,有几个过滤器输出单元就具有多少深度。
卷积层解决这类问题的一种简单方法是对隐含单元和输入单元间的连接加以限制:每个隐含单元仅仅只能连接输入单元的一部分。
例如,每个隐含单元仅仅连接输入图像的一小片相邻区域。(对于不同于图像输入的输入形式,也会有一些特别的连接到单隐含层的输入信号“连接区域”选择方式。如音频作为一种信号输入方式,一个隐含单元所需要连接的输入单元的子集,可能仅仅是一段音频输入所对应的某个时间段上的信号。)
具体如下图所示,样例输入单元大小是32×32×3, 输出单元的深度是5, 对于输出单元不同深度的同一位置,与输入图片连接的区域是相同的,但是参数(过滤器)不同。
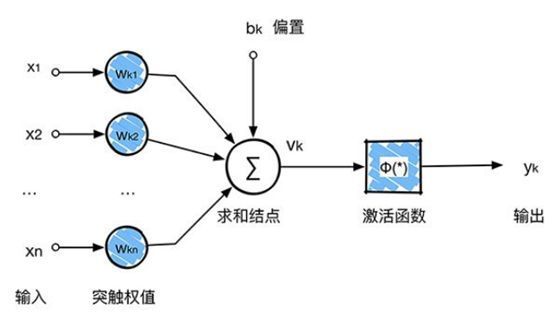
虽然每个输出单元只是连接输入的一部分,但是值的计算方法是没有变的,都是权重和输入的点积,然后加上偏置,这点与普通神经网络是一样的,如下图所示:
2) 前期准备
一个输出单元的大小有以下三个量控制:depth, stride 和 zero-padding。
- 深度(depth) : 顾名思义,它控制输出单元的深度,也就是filter的个数,连接同一块区域的神经元个数。又名:depth column
- 步幅(stride):它控制在同一深度的相邻两个隐含单元,与他们相连接的输入区域的距离。如果步幅很小(比如 stride = 1)的话,相邻隐含单元的输入区域的重叠部分会很多; 步幅很大则重叠区域变少。
- 补零(zero-padding) : 我们可以通过在输入单元周围补零来改变输入单元整体大小,从而控制输出单元的空间大小。
我们先定义几个符号:
- W W W : 输入单元的大小(宽或高)
- F F F : 感受野(receptive field)
- S S S : 步幅(stride)
- P P P : 补零(zero-padding)的数量
- K K K : 深度,输出单元的深度
则可以用以下公式计算一个维度(宽或高)内一个输出单元里可以有几个隐藏单元:
W − F + 2 P S + 1 \frac{W-F+2P}{S}+1 SW−F+2P+1
如果计算结果不是一个整数,则说明现有参数不能正好适合输入,步幅(stride)设置的不合适,或者需要补零,证明略,下面用一个例子来说明一下。
例子
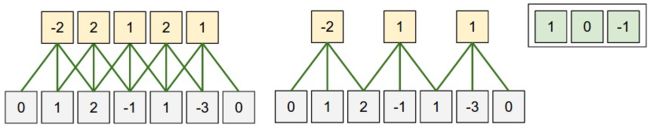
这是一个一维的例子,左边模型输入单元有5个,即 W = 5 W=5 W=5,
边界各补了一个零,即 P = 1 P=1 P=1,
步幅是1, 即 S = 1 S=1 S=1,感受野是3,
因为每个输出隐藏单元连接3个输入单元,即 F = 3 F=3 F=3,
根据上面公式可以计算出输出隐藏单元的个数是 5 − 3 + 2 1 + 1 = 5 \frac{5-3+2}{1}+1=5 15−3+2+1=5:与图示吻合。
右边那个模型是把步幅变为2,其余不变,可以算出输出大小为: 5 − 3 + 2 2 + 1 \frac{5-3+2}{2}+1 25−3+2+1,也与图示吻合。
若把步幅改为3,则公式不能整除,说明步幅为3不能恰好吻合输入单元大小。
3) 参数共享
应用参数共享可以大量减少参数数量,参数共享基于一个假设:如果图像中的一点 ( x 1 , y 1 ) (x_1,y_1) (x1,y1)包含的特征很重要,那么它应该和图像中的另一点 ( x 2 , y 2 ) (x_2,y_2) (x2,y2)一样重要。
换种说法,我们把同一深度的平面叫做深度切片(depth slice)((e.g. a volume of size [55x55x96] has 96 depth slices, each of size [55x55])),那么同一个切片应该共享同一组权重和偏置。
我们仍然可以使用梯度下降的方法来学习这些权值,只需要对原始算法做一些小的改动, 这里共享权值的梯度是所有共享参数的梯度的总和。
我们不禁会问为什么要权重共享呢?
一方面,重复单元能够对特征进行识别,而不考虑它在可视域中的位置。
另一方面,权值共享使得我们能更有效的进行特征抽取,因为它极大的减少了需要学习的自由变量的个数。通过控制模型的规模,卷积网络对视觉问题可以具有很好的泛化能力。
4) 卷积运算
如果应用参数共享的话,实际上每一层计算的操作就是输入层和权重的卷积!这也就是卷积神经网络名字的由来。
a) 二维卷积运算
先抛开卷积,这个概念不管。为简便起见,考虑一个大小为5×5的图像,和一个3×3的卷积核。
这里的卷积核共有9个参数,就记为 Θ = [ θ i j ] 3 × 3 Θ=[\theta_{ij}]_{3\times 3} Θ=[θij]3×3吧。
这种情况下,卷积核实际上有9个神经元,他们的输出又组成一个3×3的矩阵,称为特征图。
第一个神经元连接到图像的第一个3×3的局部,
第二个神经元则连接到第二个局部(注意,有重叠!就跟你的目光扫视时也是连续扫视一样)。步幅为1,每次运算,矩阵移动一个步幅
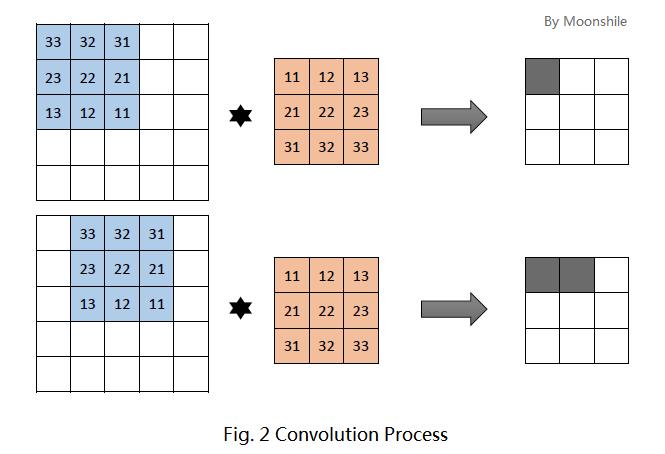
具体如下图所示。
计算过程为各个位置的卷积核的元素和输入元素的对应元素相乘,在求和
灰色方块的答案= 33 × 11 + 32 × 12 + 31 × 13 + 23 × 21 + 22 × 22 + 21 × 23 + 13 × 31 + 12 × 32 + 11 × 33 33\times 11+32\times 12+31\times 13+23\times 21+22\times 22+21\times 23+13\times 31+12\times 32+11\times 33 33×11+32×12+31×13+23×21+22×22+21×23+13×31+12×32+11×33
图的第一行是第一个神经元的输出,第二行是第二个神经元的输出。每个神经元的运算依旧是
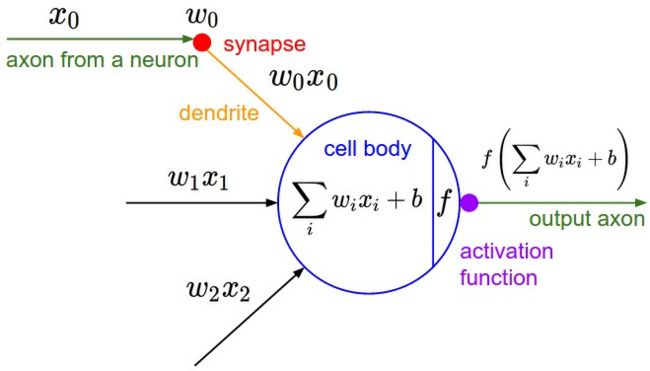
f ( x ) = a c t ( ∑ i , j n θ ( n − j ) ( n − i ) x i j + b ) f(x)=act(\sum_{i,j}^n\theta_{(n-j)(n-i)}x_{ij}+b) f(x)=act(i,j∑nθ(n−j)(n−i)xij+b)
需要注意的是,平时我们在运算时,习惯使用 θ i j x i j \theta_{ij}x_{ij} θijxij,这种写法,但事实上,我们这里使用的是 θ ( n − j ) ( n − i ) x i j \theta_{(n-j)(n-i)}x_{ij} θ(n−j)(n−i)xij
现在我们回忆一下离散卷积运算。假设有二维离散函数 f ( x , y ) , g ( x , y ) f(x,y),g(x,y) f(x,y),g(x,y)那么它们的卷积定义为
f ( m , n ) ∗ g ( m , n ) = ∑ u ∞ ∑ v ∞ f ( u , v ) g ( m − u , n − v ) f(m,n)*g(m,n)=\sum_{u}^\infty \sum_{v}^\infty f(u,v)g(m-u,n-v) f(m,n)∗g(m,n)=u∑∞v∑∞f(u,v)g(m−u,n−v)
现在发现了吧!上面例子中的9个神经元均完成输出后,实际上等价于图像和卷积核的卷积操作!
例子
输入:
4 × 4 4\times 4 4×4的图片,
过滤器 3 × 3 3\times 3 3×3,
步幅1
补零0
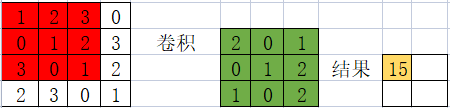
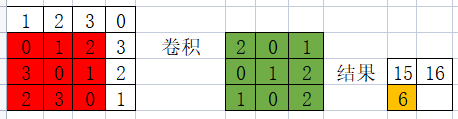
是如何算出来的???
15是下面算出来的
1 × 2 + 2 × 0 + 3 × 1 + 0 × 0 + 1 × 1 + 2 × 2 + 3 × 1 + 0 × 0 + 1 × 2 = 2 + 3 + 1 + 4 + 3 + 2 = 15 1\times 2+2\times 0+3\times 1+0\times 0+1\times 1+2\times2+3\times 1+0\times 0+1\times 2=2+3+1+4+3+2=15 1×2+2×0+3×1+0×0+1×1+2×2+3×1+0×0+1×2=2+3+1+4+3+2=15
b) 偏置
一般情况下怎么添加偏置
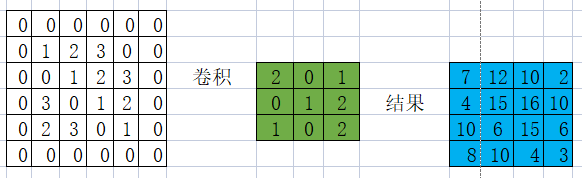
c) 填充
如果输入数据 4 × 4 4\times 4 4×4,滤波器 3 × 3 3\times 3 3×3,如果不填充 P = 0 P=0 P=0的话,输出矩阵就是 2 × 2 2\times 2 2×2
感受野一般为滤波器的大小,所以 F = 3 F=3 F=3
W − F + 2 P S + 1 = 4 − 3 + 0 1 + 1 = 2 \frac{W-F+2P}{S}+1=\frac{4-3+0}{1}+1=2 SW−F+2P+1=14−3+0+1=2
每次卷积运算,输出大小都在变小,当变成1时,无法在应用卷积运算,怎么办???
为了避免这种情况,就要使用填充
填充后
W = 4 , F = 3 , P = 1 , S = 1 W − F + 2 P S + 1 = 4 − 3 + 2 1 + 1 = 4 W=4,F=3,P=1,S=1 \\ \frac{W-F+2P}{S}+1=\frac{4-3+2}{1}+1=4 W=4,F=3,P=1,S=1SW−F+2P+1=14−3+2+1=4
d) 三维卷积运算
通道方向上有多个特征图时,会按照通道输入数据和滤波器的卷积运算,并将结果相加
5) 小结
- 接收三维输入 W ∗ H ∗ D W*H*D W∗H∗D
- 需要给出4个参数(hyperparameters):
- F F F : 感受野(receptive field)
- S S S : 步幅(stride)
- P P P : 补零(zero-padding)的数量
- K K K : 过滤器的数量
- 输出大小 W 1 ∗ H 1 ∗ D 1 W_1*H_1*D_1 W1∗H1∗D1
- W 1 = W − F + 2 P S + 1 W_1=\frac{W-F+2P}{S}+1 W1=SW−F+2P+1
- H 1 = H − F + 2 P S + 1 H_1=\frac{H-F+2P}{S}+1 H1=SH−F+2P+1
- D 1 = K D_1=K D1=K
- 应用权值共享,每个filter会产生 F ∗ F ∗ D F*F*D F∗F∗D个权值,总共 ( F ∗ F ∗ D ) ∗ K (F*F*D)*K (F∗F∗D)∗K个权重和 K K K个偏置
- 在输出单元,第d个深度切片的结果是由第d个过滤器和输入单元做卷积运算,然后再加上偏置而来。
4.2.3 池化层
参考资料
https://www.cnblogs.com/wj-1314/p/9754072.html
1) 基本概念
为了有效地减少计算量,CNN使用的另一个有效的工具被称为“池化(Pooling)”。池化就是将输入图像进行缩小,减少像素信息,只保留重要信息。
池化(pool)即下采样(downsamples),目的是为了减少特征图。
池化操作对每个深度切片独立,规模一般为 2 * 2 2*2 2*2,相对于卷积层进行卷积运算,池化层进行的运算一般有以下几种:
- 最大池化(Max Pooling)。取4个点的最大值。这是最常用的池化方法。
- 均值池化(Mean Pooling)。取4个点的均值。
- 高斯池化。借鉴高斯模糊的方法。不常用。
- 可训练池化。训练函数 ff ,接受4个点为输入,出入1个点。不常用。
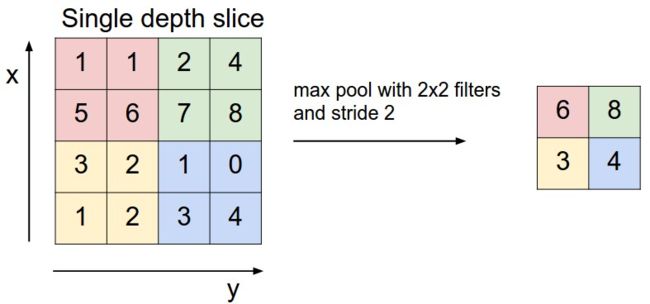
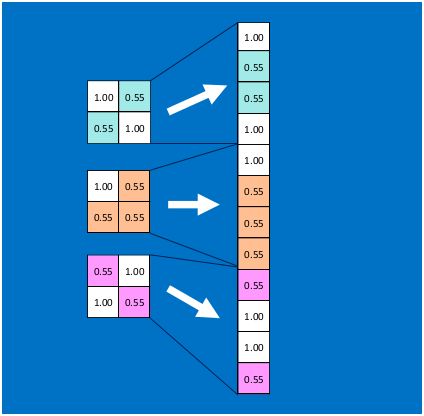
例子
最常见的池化层是规模为2*2, 步幅为2,对输入的每个深度切片进行下采样。每个MAX操作对四个数进行,如下图所示:
池化操作将保存深度大小不变。
如果池化层的输入单元大小不是二的整数倍,一般采取边缘补零(zero-padding)的方式补成2的倍数,然后再池化。
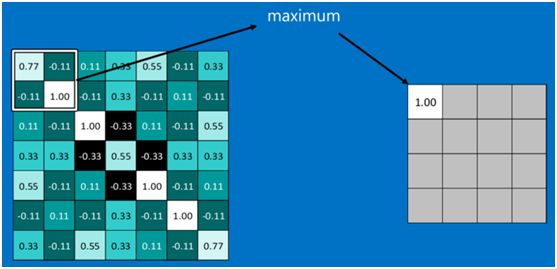
例子
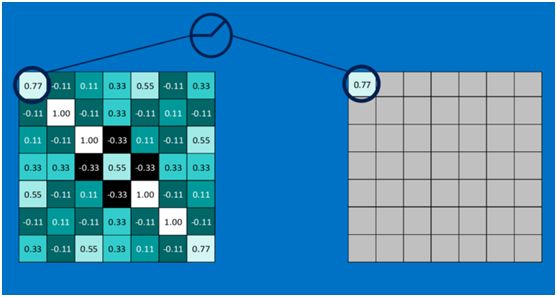
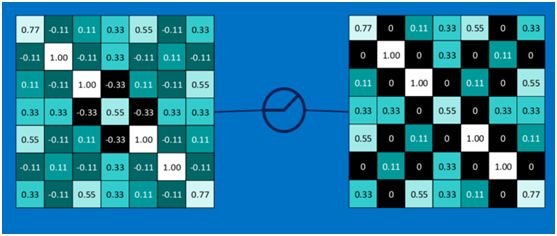
下图显示了左上角2*2池化区域的max-pooling结果,取该区域的最大值max(0.77,-0.11,-0.11,1.00),作为池化后的结果,如下图:
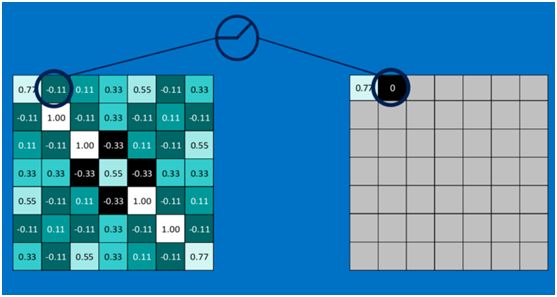
池化区域往左,第二小块取大值max(0.11,0.33,-0.11,0.33),作为池化后的结果,如下图:
其它区域也是类似,取区域内的最大值作为池化后的结果,最后经过池化后,结果如下:
2) 小结
-
接收单元大小为 W ∗ H ∗ D W*H*D W∗H∗D
-
需要两个参数(hyperparameters):
- 感受野 F F F
- 步幅 S S S
-
输出大小 W 1 ∗ H 1 ∗ D 1 W_1*H_1*D_1 W1∗H1∗D1
- W 1 = W − F S W_1=\frac{W-F}{S} W1=SW−F
- H 1 = H − F S + 1 H_1=\frac{H-F}{S}+1 H1=SH−F+1
- D 1 = D D_1=D D1=D
-
不需要引入新权重
4.2.4 全连接层
1) 基本概念
全连接层在整个卷积神经网络中起到“分类器”的作用,即通过卷积、激活函数、池化等深度网络后,再经过全连接层对结果进行识别分类。
连接层和卷积层可以相互转换:
- 对于任意一个卷积层,要把它变成全连接层只需要把权重变成一个巨大的矩阵,其中大部分都是0除了一些特定区块(因为局部感知),而且好多区块的权值还相同(由于权重共享)。
- 相反地,对于任何一个全连接层也可以变为卷积层。比如,一个 K = 4096 K=4096 K=4096的全连接层,输入层大小为 7 ∗ 7 ∗ 512 7∗7∗512 7∗7∗512,它可以等效为一个 F = 7 , P = 0 , S = 1 , K = 4096 F=7, P=0, S=1, K=4096 F=7,P=0,S=1,K=4096的卷积层。换言之,我们把 filter size 正好设置为整个输入层大小。
2) 例子
首先将经过卷积、激活函数、池化的深度网络后的结果串起来,如下图所示:
4.2.5 激活函数RelU
常用的激活函数有sigmoid、tanh、relu等等,前两者sigmoid/tanh比较常见于全连接层,后者ReLU常见于卷积层。
激活函数的作用是用来加入非线性因素,把卷积层输出结果做非线性映射。
在卷积神经网络中,激活函数一般使用ReLU(The Rectified Linear Unit,修正线性单元),它的特点是收敛快,求梯度简单。计算公式也很简单,max(0,T),即对于输入的负值,输出全为0,对于正值,则原样输出。
例子
下面看一下本案例的ReLU激活函数操作过程:
第一个值,取max(0,0.77),结果为0.77,如下图
第二个值,取max(0,-0.11),结果为0,如下图
以此类推,经过ReLU激活函数后,结果如下:
4.2.6 小结
架构简介
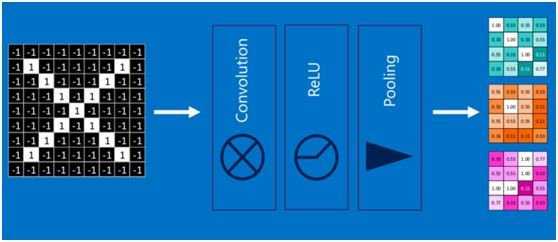
通过将上面所提到的卷积、激活函数、池化组合在一起,就变成下图:
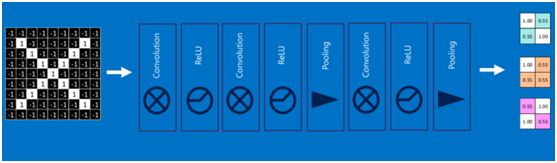
通过加大网络的深度,增加更多的层,就得到了深度神经网络,如下图:
总结
- 卷积网络在本质上是一种输入到输出的映射,它能够学习大量的输入与输出之间的映射关系,而不需要任何输入和输出之间的精确的数学表达式,只要用已知的模式对卷积网络加以训练,网络就具有输入输出对之间的映射能力。
- CNN一个非常重要的特点就是头重脚轻(越往输入权值越小,越往输出权值越多),呈现出一个倒三角的形态,这就很好地避免了BP神经网络中反向传播的时候梯度损失得太快。
- 卷积神经网络CNN主要用来识别位移、缩放及其他形式扭曲不变性的二维图形。
- 由于CNN的特征检测层通过训练数据进行学习,所以在使用CNN时,避免了显式的特征抽取,而隐式地从训练数据中进行学习;再者由于同一特征映射面上的神经元权值相同,所以网络可以并行学习,这也是卷积网络相对于神经元彼此相连网络的一大优势。卷积神经网络以其局部权值共享的特殊结构在语音识别和图像处理方面有着独特的优越性,其布局更接近于实际的生物神经网络,权值共享降低了网络的复杂性,特别是多维输入向量的图像可以直接输入网络这一特点避免了特征提取和分类过程中数据重建的复杂度。
- 将以上所有结果串起来后,就形成了一个“卷积神经网络”(CNN)结构,如下图所示:
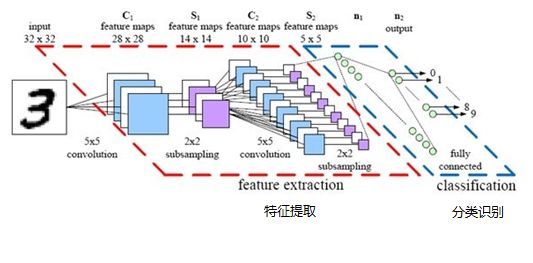
- 最后,再回顾总结一下,卷积神经网络主要由两部分组成,一部分是特征提取(卷积、激活函数、池化),另一部分是分类识别(全连接层),下图便是著名的手写文字识别卷积神经网络结构图:
4.2.7 各种计算公式
- W W W为输入
- F F F为卷积核
- P P P为padding
- S S S为strides,步长
- D D D为dilation
1) 卷积计算公式
O = W − F + 2 P S + 1 O=\frac{W-F+2P}{S}+1 O=SW−F+2P+1
2) 膨胀卷积计算公式
上述公式不变,把上面的 F F F变成下面公式中的 F ′ F^\prime F′
F ′ = D × ( F − 1 ) + 1 F^\prime=D\times (F-1)+1 F′=D×(F−1)+1
3) 池化计算公式
O = W − F + 2 P S + 1 O=\frac{W-F+2P}{S}+1 O=SW−F+2P+1
4) 转置卷积公式
O = S ( W − 1 ) − 2 P + F O=S(W-1)-2P+F O=S(W−1)−2P+F
4.3 典型CNN
4.3.1 LeNet
1) 基本概念
LeNet诞生于1994年,由深度学习三巨头之一的Yan LeCun提出,他也被称为卷积神经网络之父。LeNet主要用来进行手写字符的识别与分类,准确率达到了98%,并在美国的银行中投入了使用,被用于读取北美约10%的支票。LeNet奠定了现代卷积神经网络的基础。
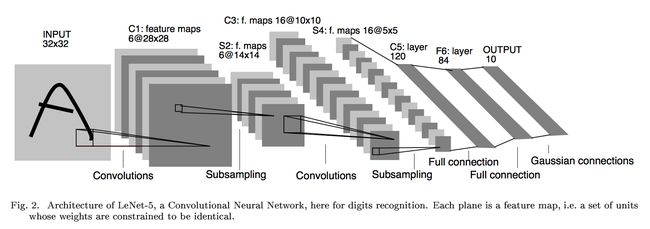
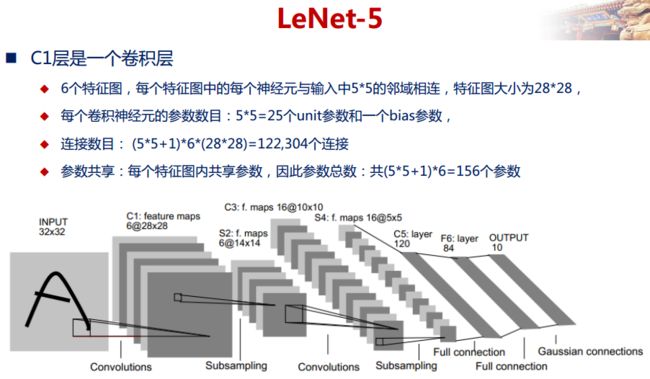
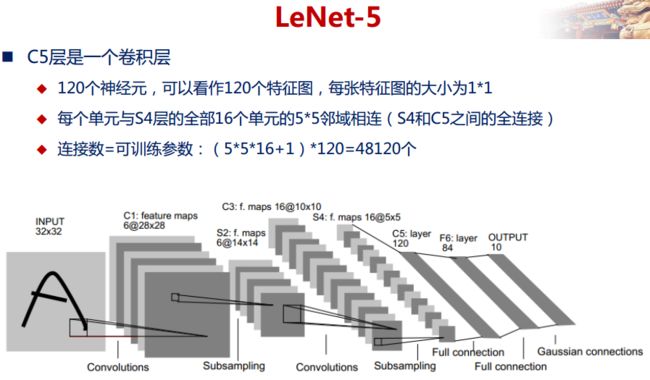
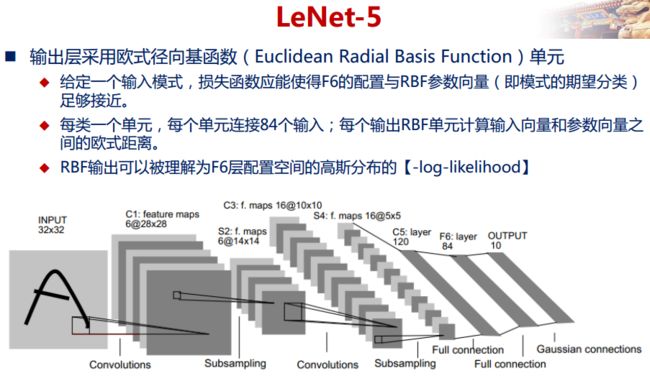
2) 网络结构
上图为LeNet结构图,是一个6层网络结构:三个卷积层,两个下采样层和一个全连接层(图中C代表卷积层,S代表下采样层,F代表全连接层)。其中,C5层也可以看成是一个全连接层,因为C5层的卷积核大小和输入图像的大小一致,都是5*5
3) 特点
- 每个卷积层包括三部分:卷积、池化和非线性激活函数(sigmoid激活函数)
- 使用卷积提取空间特征
- 降采样层采用平均池化
4.3.2 AlexNet
1) 基本概念
AlexNet由Hinton的学生Alex Krizhevsky于2012年提出,并在当年取得了Imagenet比赛冠军。
AlexNet可以算是LeNet的一种更深更宽的版本,证明了卷积神经网络在复杂模型下的有效性,算是神经网络在低谷期的第一次发声,确立了深度学习,或者说卷积神经网络在计算机视觉中的统治地位。
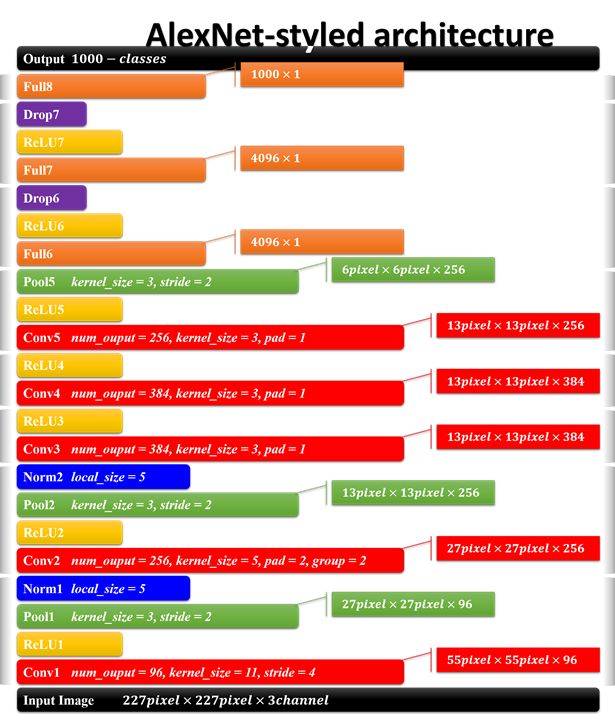
2) 网络结构
AlexNet的结构及参数如上图所示,是8层网络结构(忽略激活,池化,LRN,和dropout层),有5个卷积层和3个全连接层,第一卷积层使用大的卷积核,大小为 11 ∗ 11 11*11 11∗11,步长为4,第二卷积层使用 5 ∗ 5 5*5 5∗5的卷积核大小,步长为1,剩余卷积层都是 3 ∗ 3 3*3 3∗3的大小,步长为1。激活函数使用ReLu(虽然不是他发明,但是他将其发扬光大),池化层使用重叠的最大池化,大小为3*3,步长为2。在全连接层增加了dropout,第一次将其实用化。
3) 网络特点
- 使用两块GPU并行加速训练,大大降低了训练时间
- 成功使用ReLu作为激活函数,解决了网络较深时的梯度弥散问题
- 使用数据增强、dropout和LRN层来防止网络过拟合,增强模型的泛化能力
4.3.3 VGGNet
1) 基本概念
VGGNet是牛津大学计算机视觉组和Google DeepMind公司一起研发的深度卷积神经网络,并取得了2014年Imagenet比赛定位项目第一名和分类项目第二名。该网络主要是泛化性能很好,容易迁移到其他的图像识别项目上,可以下载VGGNet训练好的参数进行很好的初始化权重操作,很多卷积神经网络都是以该网络为基础,比如FCN,UNet,SegNet等。vgg版本很多,常用的是VGG16,VGG19网络。
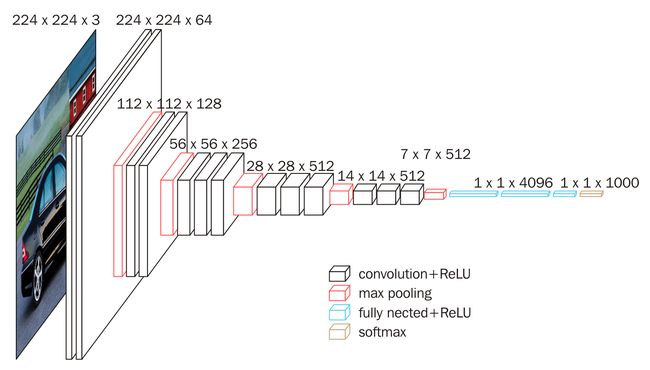
2) 网络结构
上图为VGG16的网络结构,共16层(不包括池化和softmax层),所有的卷积核都使用33的大小,池化都使用大小为22,步长为2的最大池化,卷积层深度依次为64 -> 128 -> 256 -> 512 ->512。
3) 网络特点
网络结构和AlexNet有点儿像,不同的地方在于:
- 主要的区别,一个字:深,两个字:更深。把网络层数加到了16-19层(不包括池化和softmax层),而AlexNet是8层结构。
- 将卷积层提升到卷积块的概念。卷积块有2~3个卷积层构成,使网络有更大感受野的同时能降低网络参数,同时多次使用ReLu激活函数有更多的线性变换,学习能力更强(详细介绍参考:TensorFlow实战P110页)。
- 在训练时和预测时使用Multi-Scale做数据增强。训练时将同一张图片缩放到不同的尺寸,在随机剪裁到224*224的大小,能够增加数据量。预测时将同一张图片缩放到不同尺寸做预测,最后取平均值。
4.3.4 ResNet
1) 基本概念
ResNet(残差神经网络)由微软研究院的何凯明等4名华人于2015年提出,成功训练了152层超级深的卷积神经网络,效果非常突出,而且容易结合到其他网络结构中。在五个主要任务轨迹中都获得了第一名的成绩:
- ImageNet分类任务:错误率3.57%
- ImageNet检测任务:超过第二名16%
- ImageNet定位任务:超过第二名27%
- COCO检测任务:超过第二名11%
- COCO分割任务:超过第二名12%
作为大神级人物,何凯明凭借Mask R-CNN论文获得ICCV2017最佳论文,也是他第三次斩获顶会最佳论文,另外,他参与的另一篇论文:Focal Loss for Dense Object Detection,也被大会评为最佳学生论文。
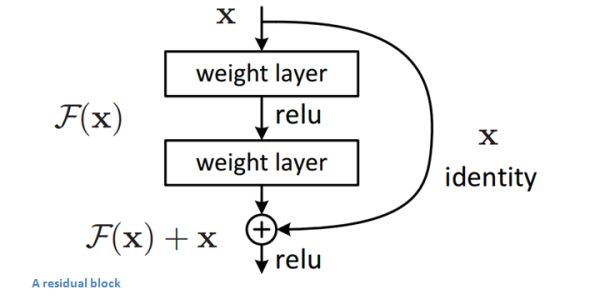
2) 网络结构
上图为残差神经网络的基本模块(专业术语叫残差学习单元),输入为x,输出为F(x)+x,F(x)代表网络中数据的一系列乘、加操作,假设神经网络最优的拟合结果输出为H(x)=F(x)+x,那么神经网络最优的F(x)即为H(x)与x的残差,通过拟合残差来提升网络效果。为什么转变为拟合残差就比传统卷积网络要好呢?因为训练的时候至少可以保证残差为0,保证增加残差学习单元不会降低网络性能,假设一个浅层网络达到了饱和的准确率,后面再加上这个残差学习单元,起码误差不会增加。
通过不断堆叠这个基本模块,就可以得到最终的ResNet模型,理论上可以无限堆叠而不改变网络的性能。下图为一个34层的ResNet网络。
3) 网络特点
- 使得训练超级深的神经网络成为可能,避免了不断加深神经网络,准确率达到饱和的现象(后来将层数增加到1000层)
- 输入可以直接连接到输出,使得整个网络只需要学习残差,简化学习目标和难度。
- ResNet是一个推广性非常好的网络结构,容易和其他网络结合