【路径规划】 The Dynamic Window Approach to Collision Avoidance (附python代码实例)

引用与前言

---

参考链接

引用参考如下：

1. 博客园解释：https://www.cnblogs.com/dlutjwh/p/11158233.html 这篇博客园写的贼棒！我当时就是一边对着论文一边对着他这篇来看的，所以==大部分论文的文字也来源于此==

2. 原文论文：https://ieeexplore.ieee.org/document/580977 没有账号的话 就去sci-hub吧，这里是preprint版：colli.dvi (cmu.edu)

3. Python代码：https://github.com/AtsushiSakai/PythonRobotics
   ROS代码：http://wiki.ros.org/dwa_local_planner

前言/基础知识

其实这篇我本科毕业论文用到了 当时很仔细的看过一遍，但是因为没有对着代码看，仅看了一下论文的数学公式推导等，就觉得很厉害，想到这样的方式去表示和限制。这次专门复习再来一次 结合着代码看一次好了。这次直接使用Typro打的markdown文件，这样在博客园的格式应该很好看了，目录也是在左边~

格式优美版在博客园，后续相关更新也在博客园内哦
虽然我感觉CSDN好像也挺优美的 hhh

首先，我们要了解这个干什么的，在路径规划算法 主要包括全局路径规划和局部路径规划。局部路径规划主要用于动态环境下的导航和避障，对于无法预测的障碍物DWA算法可以较好地解决。DWA算法的优点是计算负复杂度较低，由于考虑到速度和加速度的限制，只有安全的轨迹会被考虑，且每次采样的时间较短，因此轨迹空间较小。采样的速度即形成了一个动态窗口

直接跳转可以先看看运行的效果，感受一下

论文部分

---

介绍/Introduction

DWA的整体轨迹评价函数主要是三个方面：

1. 与目标的接近程度
2. 机器人前进的速度
3. 与下一个障碍物的距离

简而言之就是在局部规划出一条路径，希望与目标越来越近，且速度较快，与障碍物尽可能远。评价函数权衡以上三个部分得到一条最优路径。

该论文相对于之前的创新点在于：

• 该方法是由一个移动机器人的**运动动力学**推导出来的
• 考虑到机器人的惯性（代码中计算了刹车距离），这对于具有扭矩限制机器人在高速行驶时很重要。
• 在动态杂乱环境中速度可以较快，对于速度较快的机器人以及低电动机转矩的机器人较为实用。

相关工作/Related Work

这部分对比的时候，因为年代的原因是随着全局规划一起对比的

1. 全局优点在于计算时可以离线进行，但是目前ROS中全局路径也在导航过程中不断变化。
2. 全局缺点在于不能适应环境变化以及计算复杂度太高，尤其是环境不断变化时。
3. 局部缺点在于不能保证得到最优解，容易陷入局部最优（如U形障碍环境）。
4. 局部优点在于计算速度快，适合环境不断变化。
5. 对比了其他的局部路径规划算法的优缺点：势场法计算速度很快，但是在狭窄区域会产生震荡，如果目标点在两个很近的障碍物之间，则可能找不到路径。

机器人运动学方程

为了使运动学方程更加接近实际，将模型的速度设为随时间变化的分段函数，在该假设下，机器人轨迹可看做许多的圆弧积分组成，采用该方法使得障碍物碰撞检测很方便，因为圆弧与障碍物的交点很好求。

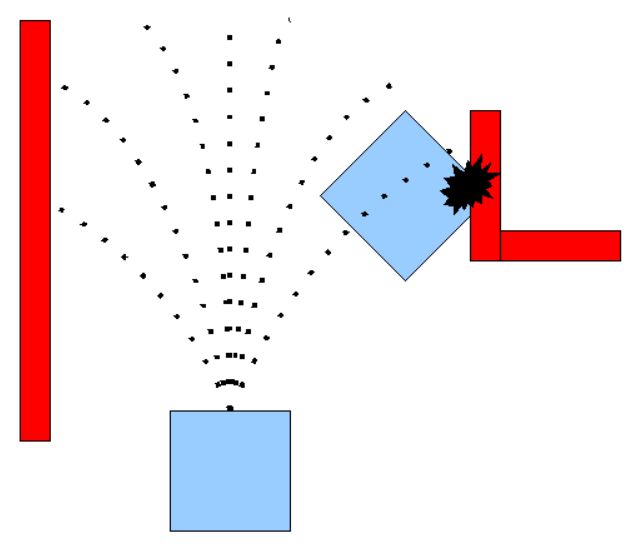
其中关于公式参数的提前解释：

• $x(t)$, $y(t)$, $\theta (t)$ 分别表示机器人在 $t$ 时刻的$x$ 坐标、$y$ 坐标以及朝向角
• $x(t_0)$, $x(t_n)$ 分别表示机器人在 $t_0$ 和 $t_1$ 时刻的$x$坐标
• $v(t)$ 表示机器人的平移速度

$$x\left(t_n\right)=x\left(t_0\right)+{\int }_{t_0}^{t_n}v(t)\cdot \cos \theta (t)dt\text{\hspace{1em}(1)}$$

$$y\left(t_n\right)=y\left(t_0\right)+{\int }_{t_0}^{t_n}v(t)\cdot \sin \theta (t)dt\text{\hspace{1em}(2)}$$

由此得知坐标是根据速度来得到的，而这个速度不能说直接给他设置，有限制的。例如，机器人速度 $v(t)$ 取决于初始时刻 $t_0$ 的速度和时间 $t_0$，和速度一样的， $\theta (t)$ 也是初始转向角 $\theta (t_0)$ 函数

• 机器人在时间间隔 $\hat{t}\in [t_0,t]$ 的平移加速度为 $\dot{v}(\hat{t})$
• $t_0$ 时刻的初始旋转速度为 $w(t_0)$，$\hat{t}\in [t_0,t]$ 的旋转加速度为 $\dot{w}(\hat{t})$，故(1)可以转为：

$$x\left(t_n\right)=x\left(t_0\right)+{\int }_{t_0}^{t_n}\left(v\left(t_0\right)+{\int }_{t_0}^t\dot{v}(\hat{t})d\hat{t}\right)\cdot \cos (\theta \left(t_0\right)+{\int }_{t_0}^t\left(\left(w\left(t_0\right)+{\int }_{t_0}^{\bar{t}}\dot{w}(\tilde{t})d\tilde{t}\right)d\tilde{t}\right)dt\text{\hspace{1em}(3)}$$

此时机器人的轨迹由初始时刻的状态以及加速度决定，可以认为这些状态是可控的，同时由于机器人内部结构原因，其加速度也不是一直变化（类似于连续函数），因此可以将 $t_0$ 到 $t_n$ 看作是很多个时间片，积分可以转换为求和，假设有$n$个时间片，在每个$[t_i,t_{i+1}]$，机器人的加速度 ${\dot{v}}_i$和$\dot{w}$ 保持不变，设${\Delta }_t^i=t-t_i$，那么(3) 又可以再一步：
$$x\left(t_n\right)=x\left(t_0\right)+\sum _{i=0}^{n-1}{\int }_{t_i}^{t_{i+1}}\left(v\left(t_i\right)+{\dot{v}}_i\cdot {\Delta }_t^i\right)\cdot \cos \left(\theta \left(t_i\right)+w\left(t_i\right)\cdot {\Delta }_t^i+\frac{1}{2}{\dot{w}}_i\cdot {\left({\Delta }_t^i\right)}^2\right)dt\text{\hspace{1em}(4)}$$
式(4)虽然与机器人的动力控制相关，但是不能决定机器人具体的驾驶方向，对于障碍物与机器人轨迹的交点也很难求出，可以继续进行简化，既然时间间隔很小，那么我们就把，那么就可以得到(5)

• $v(t_i)+{\dot{v}}_i\cdot {\Delta }_t^i$ 近似为 $v_i\in [v(t_i),v(t_{i+1})]$
• $\theta \left(t_i\right)+w\left(t_i\right)\cdot {\Delta }_t^i+\frac{1}{2}{\dot{w}}_i\cdot {\left({\Delta }_t^i\right)}^2$ 近似为 $\theta \left(t_i\right)+w\left(t_i\right)\cdot {\Delta }_t^i$

$$x\left(t_n\right)=x\left(t_0\right)+\sum _{i=0}^{n-1}{\int }_{t_i}^{t_{i+1}}{v}_i\cdot \cos \left(\theta \left(t_i\right)+w_i\ast \left(\hat{t}-t_i\right)\right)d\hat{t}\text{\hspace{1em}(5)}$$

最后解这个积分方程，简化为：
$$x\left(t_n\right)=x\left(t_0\right)+\sum _{i=0}^{n-1}{F}_x^i(t_{i+1})\text{\hspace{1em}(6)}$$
其中$F$ 展开就是：
$$F_x^i\left(t_i\right)=\{\begin{array}{l}\frac{v_i}{w_i}\left(\sin \theta \left(t_i\right)-\sin \left(\theta \left(t_i\right)+w_i\cdot \left(t-t_i\right)\right)\right),w_i\ne 0\\ v_i\cos \left(\theta \left(t_i\right)\right)\cdot t,w_i=0\end{array}\text{\hspace{1em}(7)}$$
以上都是推导$x$ 坐标，对于$y$ 整个过程也是一样的，就是$F$ 里面的一个三角函数变换了
$$y\left(t_n\right)=y\left(t_0\right)+\sum _{i=0}^{n-1}{F}_y^i(t_{i+1})\text{\hspace{1em}(8)}$$

$$F_y^i\left(t_i\right)=\{\begin{array}{l}-\frac{v_i}{w_i}\left(\cos \theta \left(t_i\right)-\cos \left(\theta \left(t_i\right)+w_i\cdot \left(t-t_i\right)\right)\right),w_i\ne 0\\ v_i\sin \left(\theta \left(t_i\right)\right)\cdot t,w_i=0\end{array}\text{\hspace{1em}(9)}$$

• 当$w_i=0$ 时，机器人行走轨迹为一条直线

• 当$w_i\ne 0$ 时，机器人轨迹为圆弧，设：
  $$M_x^i=-\frac{v_i}{w_i}\cdot \sin \theta \left(t_i\right)\text{\hspace{1em}(10)}$$

  $$M_y^i=\frac{v_i}{w_i}\cdot \cos \theta (t-i)\text{\hspace{1em}(11)}$$

  然后，奇妙的事情就发生了，我们可以得到这样一个式子：
  $${\left(F_x^i-M_x^i\right)}^2+{\left(F_x^i-M_x^i\right)}^2={\left(\frac{v_i}{w_i}\right)}^2\text{\hspace{1em}(12)}$$
  这个式子就是圆在平面的公式，其中这个圆的圆心为 $(M_x^i,M_y^i)$，半径为$\frac{v_i}{w_i}$。根据上述公式可以求出机器人的轨迹，即通过一系列分段的圆弧和直线来拟合轨迹。

误差界

将机器人轨迹进行分段会在控制点之间产生线性误差，即$t_{i+1}-t_i$之间的误差，设x坐标和y坐标的误差分别为$E_x^i$和$E_y^i$，$\Delta t_i=t_{i+1}-t_i$，由于$i\in [v(t_i),v(t_{i+1})]$，故最大误差$E_x^i,E_y^i\le |v(t_{i+1})-v(t_i)|\cdot \Delta t_i$，在$\Delta t_i$内是线性的。注意该上界误差仅仅可用于机器人内部预测，而实际机器人位置一般通过里程计测量。

动态窗口法

动态窗口法在速度空间中进行速度采样，并对随机采样的速度进行限制，减小采样数目，在使用代价函数进行评价。

1. 速度搜索空间

根据以下三点进行速度空间降采样

• 圆弧轨迹：动态窗口法仅仅考虑圆弧轨迹，该轨迹由采样速度 $(v,w)$ 决定，这些速度构成一个速度搜索空间。
• 允许速度：如果机器人能够在碰到最近的障碍物之前停止，则该采样速度将被评估。
• 动态窗口：由于机器人加速度的限制，因此只有在加速时间内能达到的速度才会被保留。

2. 最优化

代价函数方程：
$$G(v,w)=\sigma (\alpha \cdot \text{heading}(v,w)+\beta \cdot \text{dist}(v,w)+\gamma \cdot \text{vel}(v,w))\text{\hspace{1em}(13)}$$
最大值即使最优值最大，其中$\sigma$使得三个部分的权重更加平滑，使得轨迹与障碍物之间保持一定的间隙。

1. Target heading: heading用于评价机器人与目标位置的夹角，当机器人朝着目标前进时，该值取最大；举个例子：表示机器人与目标点的对齐程度，用$180-\theta$表示，$\theta$为机器人与目标夹角，夹角越大，代价值越小。

   

2. Clearance: dist 用于表示与机器人轨迹相交的最近的障碍物距离；如果障碍物与机器人轨迹不相交，则设为一个较大的值

3. Velocity: vel 表示机器人的前向移动速度，支持快速移动

安全速度

机器人能够在撞掉障碍物之前停下，$\text{dist}(v,w)$ 为机器人轨迹上与障碍物的最近距离，设刹车时的加速度为 ${\dot{v}}_b,{\dot{w}}_b$ ，则 $V_a$ 为机器人不与障碍物碰撞的速度集合：
$$V_a=\left\{v,w\mid v\le \sqrt{2\cdot \text{dist}(v,w)\cdot {\dot{v}}_b}\cap w\le \sqrt{2\ast \text{dist}(v,w)\ast {\dot{w}}_b}\right\}$$

动态窗口速度

考虑到机器人的动力加速度，搜索空间降采样到动态窗口，只保留以当前加速度可到达的速度，设$t$为时间间隔，$(v_a,w_a)$为实际速度，则动态窗口的速度集合为$V_d$：该集合以外的速度都不能在该时间间隔内达到。
$$V_d=\left\{v,w\mid v\in \left[v_a-\dot{v}\cdot t,v_a+\dot{v}\cdot t\right]\cap w\in \left[w_a-\dot{w}\cdot t,w_a+\dot{w}\cdot t\right]\right\}$$
综上，最终的搜索空间：
$$V_r=V_s\cap V_a\cap V_d$$
最终的代价函数的限制就是在这个搜索空间内的

实验部分

平滑处理：

评价函数的三个部分都被正则化在$[0,1]$上，实验中设置了$\alpha =2$，$\beta =0.2$，$\gamma =0.2$，平滑处理可以使机器人与障碍物之间有一定的间隙（裕度）。

实现细节：

• 当机器人陷入局部最优时（即不存在路径可以通过），使其原地旋转，直到找到可行路径。
• 安全裕度：在路径规划时，设定一安全裕度，即在路径和障碍物之间保留一定间隙，且该间隙随着速度增大线性增长。

参数设定：

• $\alpha$ 占比重太大，机器人运动自由度大，窄的区域不容易通过，$\alpha$占比重太小，机器人轨迹则不够平滑。因此$\alpha$ 越大，越适合在窄区域，$\alpha$ 越小，越适合在宽区域。

代码部分

---

这里先说一下整体的思路，主要是对着参考的Python代码的，有空我把ROS_wiki那边也补充完整

1. 设定初始状态：$[x,y,\theta ,v,\omega ]$ ；目标位置：$[x_{goal},y_{goal}]$
2. 机器人的参数：最大最小速度、最大转角(偏航角)速度、最大加速度、最大角加速度、速度和偏航角分辨率、预测时间范围（就是生成多大的空间）、目标，速度，障碍物的各个cost设定、各个障碍物的位置
3. 计算动态窗口
4. 计算控制和轨迹点

1. 计算动态窗口

主要是根据现在的状态和默认的参数进行的设置：

def calc_dynamic_window(x, config):
    """
    calculation dynamic window based on current state x
    """

    # Dynamic window from robot specification
    Vs = [config.min_speed, config.max_speed,
          -config.max_yaw_rate, config.max_yaw_rate]

    # Dynamic window from motion model
    Vd = [x[3] - config.max_accel * config.dt,
          x[3] + config.max_accel * config.dt,
          x[4] - config.max_delta_yaw_rate * config.dt,
          x[4] + config.max_delta_yaw_rate * config.dt]

    #  [v_min, v_max, yaw_rate_min, yaw_rate_max]
    dw = [max(Vs[0], Vd[0]), min(Vs[1], Vd[1]),
          max(Vs[2], Vd[2]), min(Vs[3], Vd[3])]

    return dw

可以从中看出 主要是速度的整个窗口，读取机器人的默认速度配置，然后计算加速度时间后的速度取最小最大的，形成一个取速度的范围

2. 采样轨迹

根据现在的状态和前面的速度动态窗口，配置中的速度分辨率（就是以多少间隔生成速度值）

# evaluate all trajectory with sampled input in dynamic window
# for v in np.arange(dw[0], dw[1], config.v_resolution):
#     for y in np.arange(dw[2], dw[3], config.yaw_rate_resolution):
#         trajectory = predict_trajectory(x_init, v, y, config)

def predict_trajectory(x_init, v, y, config):
    """
    predict trajectory with an input
    """

    x = np.array(x_init)
    trajectory = np.array(x)
    time = 0
    while time <= config.predict_time:
        x = motion(x, [v, y], config.dt)
        trajectory = np.vstack((trajectory, x))
        time += config.dt

    return trajectory

其中motion就是由车辆运动的模型得出来的这时刻状态加速度得到下一时刻的状态，根据前面可知：v是速度，y是yaw角速度，x的各个位置为：$[x,y,\theta ,v,\omega ]$

def motion(x, u, dt):
    """
    motion model
    """

    x[2] += u[1] * dt # v=v+a*t
    x[0] += u[0] * math.cos(x[2]) * dt # x=x+v*cos(theta)
    x[1] += u[0] * math.sin(x[2]) * dt # y=y+v*sin(theta)
    x[3] = u[0]
    x[4] = u[1]

    return x

3. 计算cost

goal cost

这个cost也就是前面最优化里面提到的heading cost，朝向

def calc_to_goal_cost(trajectory, goal):
    """
        calc to goal cost with angle difference
    """

    dx = goal[0] - trajectory[-1, 0]
    dy = goal[1] - trajectory[-1, 1]
    error_angle = math.atan2(dy, dx)
    cost_angle = error_angle - trajectory[-1, 2]
    cost = abs(math.atan2(math.sin(cost_angle), math.cos(cost_angle)))

    return cost

速度cost

速度cost之间是根据得出的轨迹的速度和最大速度做个差值再乘一个速度cost的系数得出来的

speed_cost = config.speed_cost_gain * (config.max_speed - trajectory[-1, 3])

障碍物cost

这么一看 果然还是圆形比较适合做碰撞检测，怪不得杰哥中间也是将车膨胀成两个圆

def calc_obstacle_cost(trajectory, ob, config):
    """
    calc obstacle cost inf: collision
    """
    ox = ob[:, 0]
    oy = ob[:, 1]
    dx = trajectory[:, 0] - ox[:, None]
    dy = trajectory[:, 1] - oy[:, None]
    r = np.hypot(dx, dy)

    if config.robot_type == RobotType.rectangle:
        yaw = trajectory[:, 2]
        rot = np.array([[np.cos(yaw), -np.sin(yaw)], [np.sin(yaw), np.cos(yaw)]])
        rot = np.transpose(rot, [2, 0, 1])
        local_ob = ob[:, None] - trajectory[:, 0:2]
        local_ob = local_ob.reshape(-1, local_ob.shape[-1])
        local_ob = np.array([local_ob @ x for x in rot])
        local_ob = local_ob.reshape(-1, local_ob.shape[-1])
        upper_check = local_ob[:, 0] <= config.robot_length / 2
        right_check = local_ob[:, 1] <= config.robot_width / 2
        bottom_check = local_ob[:, 0] >= -config.robot_length / 2
        left_check = local_ob[:, 1] >= -config.robot_width / 2
        if (np.logical_and(np.logical_and(upper_check, right_check),
                           np.logical_and(bottom_check, left_check))).any():
            return float("Inf")
    elif config.robot_type == RobotType.circle:
        if np.array(r <= config.robot_radius).any():
            return float("Inf")

    min_r = np.min(r)
    return 1.0 / min_r  # OK

这一步直接计算了所有的障碍物的，也得益于python的方便，直接计算轨迹与各个障碍物的直线距离，判断是否对于圆半径，只要有一个障碍物碰到了 这条轨迹就被抛弃了，如果没有的话 输出最小的那个距离，然后分之一进行输出以便计算cost

综合下来就是：

# calc cost
to_goal_cost = config.to_goal_cost_gain * calc_to_goal_cost(trajectory, goal)
speed_cost = config.speed_cost_gain * (config.max_speed - trajectory[-1, 3])
ob_cost = config.obstacle_cost_gain * calc_obstacle_cost(trajectory, ob, config)

final_cost = to_goal_cost + speed_cost + ob_cost

运行示意

在原基础上，把其他速度窗口内的轨迹也画出来了，但是因为选cost最小的也就是红色那个哈

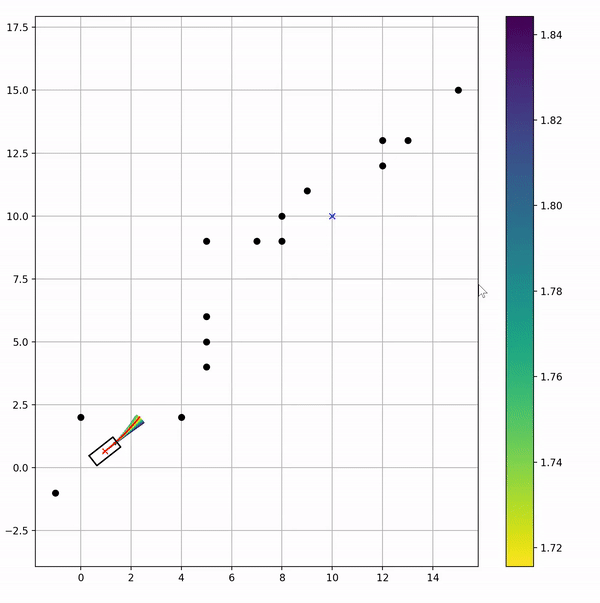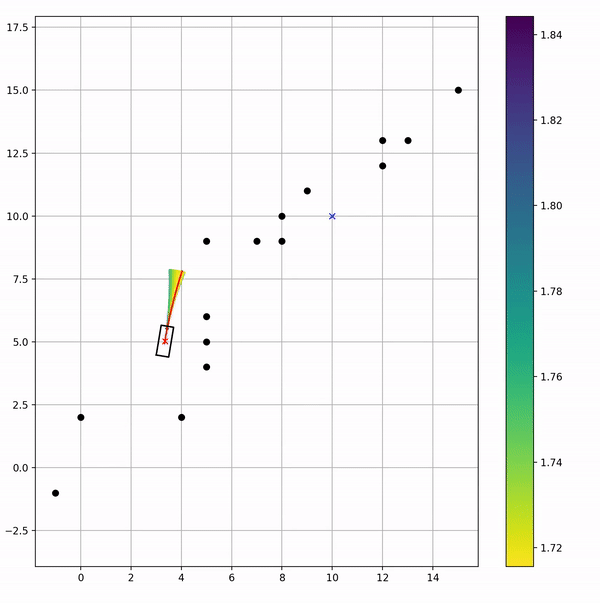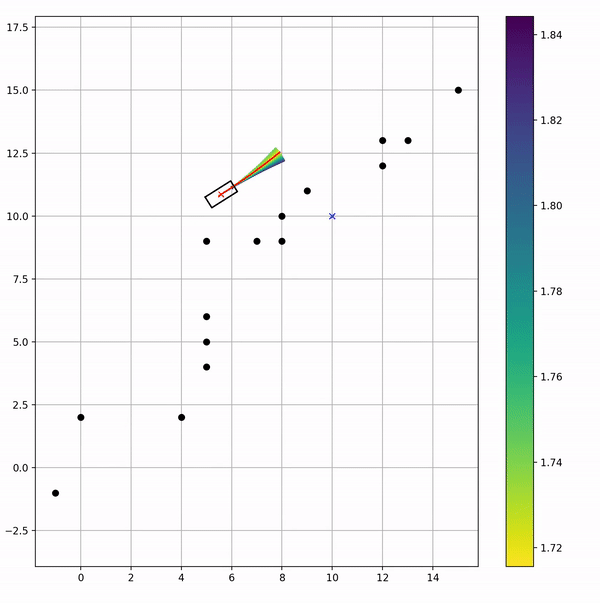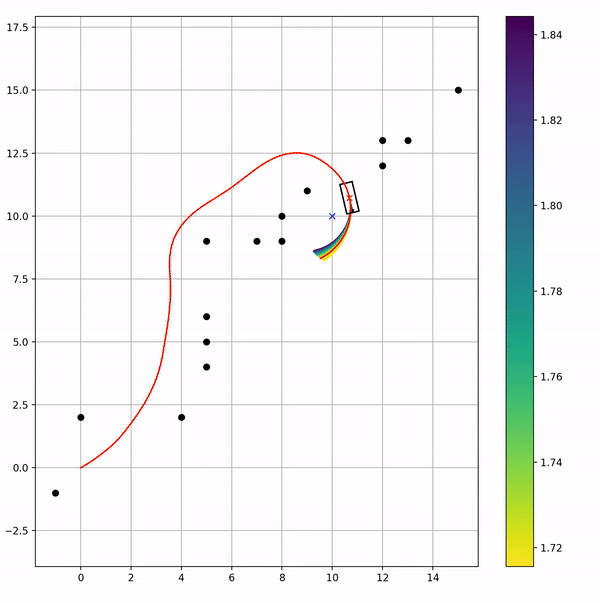
这么一看我好像知道我曾经用ROS DWA那边有啥问题了 刷新路径dt太快了？走一下发现下一步的轨迹需要左移，然后右移，然后左移 emmm 这样就S形了？或者是把障碍物的cost因子调低一点？好像是看到了就躲一下，进了再躲一下；然后再贴一下ROS那边的（我找到了我本科毕设答辩的PPT截图出来的 hhh）其实当时我答辩录屏了，但是当时录制的时候忘记点语音了 然后就是无声的，hhh 留个留念的机会都没有了

总结

---

这么一看 比frenet简单太多了 hhhh 毕竟是1997年的了，frenet都是2010年的了：Frenet 博客园的论文阅读与代码实例

主要在于：

1. DWA这篇的空间一直以笛卡尔坐标系，也不没有sd坐标系 说有什么固定的线，也正是因为如此DWA通常作为小型室内无明确道路的机器人首选的局部规划器
2. frenet那篇以考虑加加速度 jerk来作为cost，考虑了车辆乘坐时的舒适度就是加速度的加速度
3. Frenet考虑了沿着某个道路的采样方式，也就是说有某个固定道路线去做行驶，遇到障碍物了再避障，这也符合我们实际驾驶道路车的行为
4. Frenet考虑障碍物的东西更多，纵向运动时的跟车，汇入等等 所以常常作为道路无人车局部采样规划的首选

至此，再次“复习”完一个，这么看当初问阿冰哥的答案也能更懂了：

1. DWA是采样评价，大部分采样拟合再评价的都是
2. Frenet也是，OpenPlanner也是，只是说采样空间变了而已
3. 采样-拟合-评价一般说采样空间是暴力遍历的，不暴力遍历的话可以当成搜索问题