Python吴恩达深度学习作业3 - 1层隐藏层的神经网络

用1层隐藏层的神经网络分类二维数据

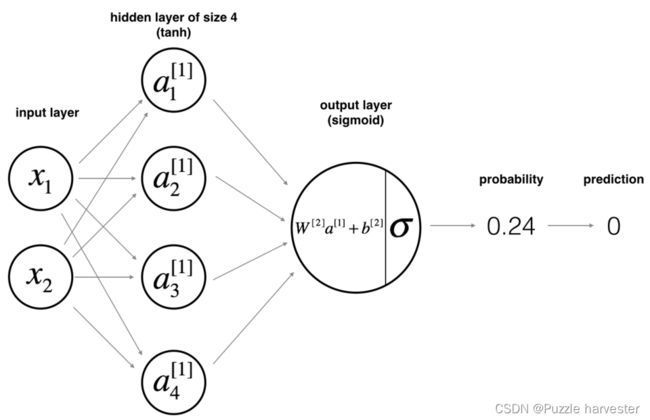
现在是时候建立你的第一个神经网络了，它将具有一层隐藏层。你将看到此模型与你使用逻辑回归实现的模型之间的巨大差异。

你将学到如何：

• 实现具有单个隐藏层的2分类神经网络
• 使用具有非线性激活函数的神经元，例如tanh
• 计算交叉熵损失
• 实现前向和后向传播

1- 安装包

让我们首先导入在作业过程中需要的所有软件包。

• numpy是Python科学计算的基本包。
• sklearn提供了用于数据挖掘和分析的简单有效的工具。
• matplotlib 是在Python中常用的绘制图形的库。
• testCases提供了一些测试示例用以评估函数的正确性
• planar_utils提供了此作业中使用的各种函数

import numpy as np
import matplotlib.pyplot as plt
from testCases import *
import sklearn
import sklearn.datasets
import sklearn.linear_model
from planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets

%matplotlib inline

np.random.seed(1) 

2- 数据集

首先，让我们获取处理的数据集。以下代码会将"flower"2分类数据集加载到变量X和Y中。

X, Y = load_planar_dataset()

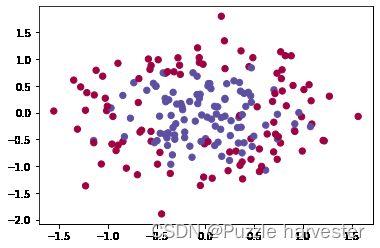
使用matplotlib可视化数据集。 数据看起来像是带有一些红色（标签y = 0）和一些蓝色（y = 1）点的“花”。 我们的目标是建立一个适合该数据的分类模型。

plt.scatter(X[0, :], X[1, :], c = Y.reshape(X[0, :].shape), s = 40, cmap = plt.cm.Spectral)

现在你有：

• 包含特征(x1, x2)的numpy数组（矩阵）X
• 包含标签（红色：0，蓝色：1）的numpy数组（向量）Y。

首先让我们深入地了解一下我们的数据。

练习：数据集中有多少个训练示例？另外，变量X和Y的shape是什么？

提示：如何获得numpy数组的shape维度？

shape_X = X.shape
shape_Y = Y.shape

m = shape_X[1] # 训练数据集大小

print ('The shape of X is: ' + str(shape_X))
print ('The shape of Y is: ' + str(shape_Y))
print ('I have m = %d training examples!' % (m))

The shape of X is: (2, 400)
The shape of Y is: (1, 400)
I have m = 400 training examples!

3- 简单Logistic回归

在构建完整的神经网络之前，首先让我们看看逻辑回归在此问题上的表现。 你可以使用sklearn的内置函数来执行此操作。 运行以下代码以在数据集上训练逻辑回归分类器。

clf = sklearn.linear_model.LogisticRegressionCV()
clf.fit(X.T, Y.T)

d:\vr\virtual_environment\lib\site-packages\sklearn\utils\validation.py:993: DataConversionWarning: A column-vector y was passed when a 1d array was expected. Please change the shape of y to (n_samples, ), for example using ravel().
  y = column_or_1d(y, warn=True)





LogisticRegressionCV()

现在，你可以运行下面的代码以绘制此模型的决策边界：

plot_decision_boundary(lambda x:clf.predict(x), X, Y)
plt.title("Logistic Regression")

LR_predictions = clf.predict(X.T)
print ('Accuracy of logistic regression: %d ' % float((np.dot(Y,LR_predictions) + np.dot(1-Y,1-LR_predictions))/float(Y.size)*100) +
       '% ' + "(percentage of correctly labelled datapoints)")

Accuracy of logistic regression: 47 % (percentage of correctly labelled datapoints)

4- 神经网络模型

从上面我们可以得知Logistic回归不适用于“flower数据集”。现在你将训练带有单个隐藏层的神经网络。

这是我们的模型：

数学原理：
例如$x^{(i)}$：
$$z^{[1](i)}=W^{[1]}{x}^{(i)}+b^{[1](i)}\text{\hspace{1em}(1)}$$
$$a^{[1](i)}=\tanh (z^{[1](i)})\text{\hspace{1em}(2)}$$
$$z^{[2](i)}=W^{[2]}{a}^{[1](i)}+b^{[2](i)}\text{\hspace{1em}(3)}$$
$${\hat{y}}^{(i)}=a^{[2](i)}=\sigma (z^{[2](i)})\text{\hspace{1em}(4)}$$
$$y_{prediction}^{(i)}=\{\begin{array}{ll}1& a^{[2](i)}>0.5\\ 0& otherwise\end{array}\text{\hspace{1em}(5)}$$

根据所有的预测数据，你还可以如下计算损失$J$:
$$J=-\frac{1}{m}\sum _{i=0}^m\left(y^{(i)}\log \left(a^{[2](i)}\right)+(1-y^{(i)})\log \left(1-a^{[2](i)}\right)\right)\text{\hspace{1em}(6)}$$

提示：
建立神经网络的一般方法是：

1. 定义神经网络结构（输入单元数，隐藏单元数等）。
2. 初始化模型的参数
3. 循环：
   • 实现前向传播
   • 计算损失
   • 后向传播以获得梯度
   • 更新参数（梯度下降）

我们通常会构建辅助函数来计算第1-3步，然后将他们合并为nn_model()函数。一旦构建了nn_model()并学习了正确的参数，就可以对新数据进行预测。

4.1- 定义神经网络结构

练习：定义三个变量：

• n_x：输入层的大小
• n_h：隐藏层的大小（将其设置为4）
• n_y：输出层的大小

提示：使用shape来找到n_x和n_y。另外，将隐藏层大小硬编码为4。

def layer_sizes(X, Y):
    n_x = X.shape[0]
    n_h = 4
    n_y = Y.shape[0]
    
    return (n_x, n_h, n_y)

X_assess, Y_assess = layer_sizes_test_case()
(n_x, n_h, n_y) = layer_sizes(X_assess, Y_assess)
print("The size of the input layer is: n_x = " + str(n_x))
print("The size of the hidden layer is: n_h = " + str(n_h))
print("The size of the output layer is: n_y = " + str(n_y))

The size of the input layer is: n_x = 5
The size of the hidden layer is: n_h = 4
The size of the output layer is: n_y = 2

4.2- 初始化模型的参数

练习：实现函数 initialize_parameters()。

说明：

• 请确保参数大小正确。 如果需要，也可参考上面的神经网络图。
• 使用随机值初始化权重矩阵。
  • 使用：np.random.randn（a，b）* 0.01随机初始化维度为（a，b）的矩阵。
• 将偏差向量初始化为零。
  • 使用：np.zeros((a,b)) 初始化维度为（a，b）零的矩阵。

def initialize_parameters(n_x, n_h, n_y):
    np.random.seed(2)
    
    W1 = np.random.randn(n_h, n_x) * 0.01
    b1 = np.zeros((n_h, 1))
    W2 = np.random.randn(n_y, n_h) * 0.01
    b2 = np.zeros((n_y, 1))
    
    assert (W1.shape == (n_h, n_x))
    assert (b1.shape == (n_h, 1))
    assert (W2.shape == (n_y, n_h))
    assert (b2.shape == (n_y, 1))
    
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    
    return parameters

n_x, n_h, n_y = initialize_parameters_test_case()

parameters = initialize_parameters(n_x, n_h, n_y)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))

W1 = [[-0.00416758 -0.00056267]
 [-0.02136196  0.01640271]
 [-0.01793436 -0.00841747]
 [ 0.00502881 -0.01245288]]
b1 = [[0.]
 [0.]
 [0.]
 [0.]]
W2 = [[-0.01057952 -0.00909008  0.00551454  0.02292208]]
b2 = [[0.]]

4.3- 循环

问题：实现forward_propagation()。

说明:

• 在上方查看分类器的数学表示形式。
• 你可以使用内置在笔记本中的sigmoid()函数。
• 你也可以使用numpy库中的np.tanh()函数。
• 必须执行以下步骤：
  1. 使用parameters [“ …”]从字典“ parameters”（这是initialize_parameters（）的输出）中检索出每个参数。
  2. 实现正向传播，计算$Z^{[1]}$,$A^{[1]}$,$Z^{[2]}$和$A^{[2]}$（所有训练数据的预测结果向量）。
     向后传播所需的值存储在cache中， cache将作为反向传播函数的输入。

def forward_propagation(X, parameters):
    """
    参数：
    X -- 输入数据大小(n_x, m)
    parameters -- 包含参数的Python字典(初始化函数的输出)
    
    返回值：
    A2 -- 用的是sigmoid函数作为输出层的激活函数
    cache -- 包含“Z1”、“A1”、“Z2”和“A2”的字典
    """
    
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    
    Z1 = np.dot(W1, X) + b1
    A1 = np.tanh(Z1)
    Z2 = np.dot(W2, A1) + b2
    A2 = sigmoid(Z2)
    
    assert(A2.shape == (1, X.shape[1]))
    
    cache = {"Z1": Z1,
             "A1": A1,
             "Z2": Z2,
             "A2": A2}
    
    return A2, cache

X_assess, parameters = forward_propagation_test_case()

A2, cache = forward_propagation(X_assess, parameters)

print(np.mean(cache['Z1']) ,np.mean(cache['A1']),np.mean(cache['Z2']),np.mean(cache['A2']))

-0.0004997557777419913 -0.0004969633532317802 0.0004381874509591466 0.500109546852431

现在，你已经计算了包含每个示例的$a^{[2](i)}$的$A^{[2]}$（在Python变量"A2"中），其中，你可以计算损失函数如下：
$$J=-\frac{1}{m}\sum _{i=0}^m(y^{(i)}\log \left(a^{[2](i)}\right)+(1-y^{(i)})\log \left(1-a^{[2](i)}\right))\text{\hspace{1em}(13)}$$

练习：实现compute_cost()以计算损失$J$的值。
说明：

• 有很多种方法可以实现交叉熵损失。 我们为你提供了实现方法：
  $-\sum _{i=0}^m{y}^{(i)}\log (a^{[2](i)})$:

logprobs = np.multiply(np.log(A2),Y)
cost = - np.sum(logprobs)                # no need to use a for loop!

（你也可以使用np.multiply()然后使用np.sum()或直接使用np.dot()）。

def compute_cost(A2, Y, parameters):
    
    m = Y.shape[1]
    
    logprobs = Y * np.log(A2) + (1 - Y) * np.log(1 - A2)
    cost = -1 / m * np.sum(logprobs)
    
    cost = np.squeeze(cost)
    
    assert(isinstance(cost, float))
    return cost

A2, Y_assess, parameters = compute_cost_test_case()

print("cost = " + str(compute_cost(A2, Y_assess, parameters)))

cost = 0.6929198937761265

现在，通过使用正向传播期间计算的缓存，你可以实现后向传播。
问题：实现函数backward_propagation()。

说明：反向传播通常是深度学习中最难（最数学）的部分。为了帮助你更好地了解，我们提供了反向传播课程的幻灯片。你将要使用此幻灯片右侧的六个方程式以构建向量化实现。

$\frac{\partial J}{\partial z_2^{(i)}}=\frac{1}{m}(a^{[2](i)}-y^{(i)})$

$\frac{\partial J}{\partial W_2}=\frac{\partial J}{\partial z_2^{(i)}}{a}^{[1](i)T}$

$\frac{\partial J}{\partial b_2}={\sum }_i\frac{\partial J}{\partial z_2^{(i)}}$

$\frac{\partial J}{\partial z_1^{(i)}}=W_2^T\frac{\partial J}{\partial z_2^{(i)}}\ast (1-a^{[1](i)2})$

$\frac{\partial J}{\partial W_1}=\frac{\partial J}{\partial z_1^{(i)}}{X}^T$

$\frac{\partial J_i}{\partial b_1}={\sum }_i\frac{\partial J}{\partial z_1^{(i)}}$

• 请注意， 表示元素乘法。
• 你将使用在深度学习中很常见的编码表示方法：
  • dW1 = $\frac{\partial J}{\partial W_1}$
  • db1 = $\frac{\partial J}{\partial b_1}$
  • dW2 = $\frac{\partial J}{\partial W_2}$
  • db2 = $\frac{\partial J}{\partial b_2}$
• 提示：
  • 要计算dZ1，你首先需要计算 $g^{[1{]}^{\prime }}(Z^{[1]})$。由于$g^{[1]}(.)$是tanh激活函数，因此如果$a=g^{[1]}(z)$则$g^{[1{]}^{\prime }}(z)=1-a^2$。所以你可以使用(1 - np.power(A1, 2))计算$g^{[1{]}^{\prime }}(Z^{[1]})$。

def backward_propagation(parameters, cache, X, Y):
    """
    参数：
        parameters -- 包含参数的Python字典
        cache -- 包含“Z1”、“A1”、“Z2”和“A2”的字典。
        X -- 输入数据大小(2, 样例数)
        Y -- “true”标签的形状向量(1, 样例数)
    返回值：
        grads -- 包含不同参数梯度的Python字典
    """
    
    W1 = parameters["W1"]
    W2 = parameters["W2"]
    
    A1 = cache["A1"]
    A2 = cache["A2"]
    
    dZ2 = A2 - Y
    dW2 = 1 / m * np.dot(dZ2, A1.T)
    db2 = 1 / m * np.sum(dZ2, axis = 1, keepdims = True)
    dZ1 = np.dot(W2.T, dZ2) * (1 - np.power(A1, 2))
    dW1 = 1 / m * np.dot(dZ1, X.T)
    db1 = 1 / m * np.sum(dZ1, axis = 1, keepdims = True)
    
    
    grads = {"dW1": dW1,
             "db1": db1,
             "dW2": dW2,
             "db2": db2}
    
    return grads

parameters, cache, X_assess, Y_assess = backward_propagation_test_case()

grads = backward_propagation(parameters, cache, X_assess, Y_assess)
print ("dW1 = "+ str(grads["dW1"]))
print ("db1 = "+ str(grads["db1"]))
print ("dW2 = "+ str(grads["dW2"]))
print ("db2 = "+ str(grads["db2"]))

dW1 = [[ 7.64031222e-05 -5.31526069e-05]
 [ 6.55085623e-05 -4.55760073e-05]
 [-3.98134983e-05  2.77034561e-05]
 [-1.65477342e-04  1.15134485e-04]]
db1 = [[-5.22957353e-06]
 [-4.54546847e-06]
 [ 2.72996662e-06]
 [ 1.13405247e-05]]
dW2 = [[ 2.72709941e-05  2.36520302e-04  8.72185240e-05 -9.88737100e-05]]
db2 = [[0.00049421]]

问题：实现参数更新。 使用梯度下降，你必须使用（dW1，db1，dW2，db2）才能更新（W1，b1，W2，b2）。

一般的梯度下降规则：$ \theta = \theta - \alpha \frac{\partial J }{ \partial \theta }$其中$\alpha$是学习率，而$\theta$代表一个参数。

图示：具有良好的学习速率（收敛）和较差的学习速率（发散）的梯度下降算法。

def update_parameters(parameters, grads, learning_rate = 1.2):
    
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    
    dW1 = grads["dW1"]
    db1 = grads["db1"]
    dW2 = grads["dW2"]
    db2 = grads["db2"]
    
    W1 = W1 - learning_rate * dW1
    b1 = b1 - learning_rate * db1
    W2 = W2 - learning_rate * dW2
    b2 = b2 - learning_rate * db2
    
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    
    return parameters

parameters, grads = update_parameters_test_case()
parameters = update_parameters(parameters, grads)

print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))

W1 = [[-0.00643025  0.01936718]
 [-0.02410458  0.03978052]
 [-0.01653973 -0.02096177]
 [ 0.01046864 -0.05990141]]
b1 = [[-1.02420756e-06]
 [ 1.27373948e-05]
 [ 8.32996807e-07]
 [-3.20136836e-06]]
W2 = [[-0.01041081 -0.04463285  0.01758031  0.04747113]]
b2 = [[0.00010457]]

4.4- 在nn_model（）中集成4.1、4.2和4.3部分中的函数

问题：在nn_model()中建立你的神经网络模型。

说明：神经网络模型必须正确的顺序组合先前构建的函数。

def nn_model(X, Y, n_h, num_iterations = 10000, print_cost = False):
    np.random.seed(3)
    
    n_x = layer_sizes(X, Y)[0]
    n_y = layer_sizes(X, Y)[2]
    
    parameters = initialize_parameters(n_x, n_h, n_y)
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    
    for i in range(0, num_iterations):
        
        A2, cache = forward_propagation(X, parameters)
        
        cost = compute_cost(A2, Y, parameters)
        
        grads = backward_propagation(parameters, cache, X, Y)
        
        parameters = update_parameters(parameters, grads)
        
        if print_cost and i % 1000 == 0:
            print ("Cost after iteration %i: %f" %(i, cost))
    return parameters

X_assess, Y_assess = nn_model_test_case()

parameters = nn_model(X_assess, Y_assess, 4, num_iterations=10000, print_cost=False)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))

d:\vr\virtual_environment\lib\site-packages\ipykernel_launcher.py:5: RuntimeWarning: divide by zero encountered in log
  """


W1 = [[-2.83554662  1.72205388]
 [-3.37802227  0.92947318]
 [-2.54331167  2.02087066]
 [ 3.37518445 -0.93029167]]
b1 = [[ 1.3407194 ]
 [ 1.67353851]
 [ 1.23099392]
 [-1.67347162]]
W2 = [[-43.10905352 -43.84863143 -42.31070324  43.80751756]]
b2 = [[-0.93568323]]

4.5- 预测

问题：使用你的模型通过构建predict()函数进行预测。

使用正向传播来预测结果。

提示：predictions = $y_{prediction}=1\text{activation > 0.5}=\{\begin{array}{ll}1& \text{if}activation>0.5\\ 0& \text{otherwise}\end{array}$

例如，如果你想基于阈值将矩阵X设为0和1，则可以执行以下操作： X_new = (X > threshold)

round()函数：
一般该函数遵循四舍五入原则，但是需要特别注意的是，当整数部分以0结束时，round函数一律是向下取整。

def predict(parameters, X):
    
    A2, cache = forward_propagation(X, parameters)
    predictions = np.round(A2)
    
    return predictions

parameters, X_assess = predict_test_case()

predictions = predict(parameters, X_assess)
print("predictions mean = " + str(np.mean(predictions)))

predictions mean = 0.6666666666666666

现在运行模型以查看其如何在二维数据集上运行。运行以下代码以使用含有隐藏单元的单个隐藏层测试模型。

parameters = nn_model(X, Y, n_h = 4, num_iterations = 10000, print_cost=True)
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
plt.title("Decision Boundary for hidden layer size " + str(4))

Cost after iteration 0: 0.693048
Cost after iteration 1000: 0.288083
Cost after iteration 2000: 0.254385
Cost after iteration 3000: 0.233864
Cost after iteration 4000: 0.226792
Cost after iteration 5000: 0.222644
Cost after iteration 6000: 0.219731
Cost after iteration 7000: 0.217504
Cost after iteration 8000: 0.219440
Cost after iteration 9000: 0.218553





Text(0.5, 1.0, 'Decision Boundary for hidden layer size 4')

predictions = predict(parameters, X)
print ('Accuracy: %d' % float((np.dot(Y,predictions.T) + np.dot(1-Y,1-predictions.T))/float(Y.size)*100) + '%')

Accuracy: 90%

与Logistic回归相比，准确性确实更高。 该模型学习了flower的叶子图案！ 与逻辑回归不同，神经网络甚至能够学习非线性的决策边界。

现在，让我们尝试几种不同的隐藏层大小。

4.6- 调整隐藏层大小

运行以下代码（可能需要1-2分钟）， 你将观察到不同大小隐藏层的模型的不同表现。

plt.figure(figsize=(16, 32))
hidden_layer_sizes = [1, 2, 3, 4, 5, 10, 20]
for i, n_h in enumerate(hidden_layer_sizes):
    plt.subplot(5, 2, i+1)
    plt.title('Hidden Layer of size %d' % n_h)
    parameters = nn_model(X, Y, n_h, num_iterations = 5000)
    plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
    predictions = predict(parameters, X)
    accuracy = float((np.dot(Y,predictions.T) + np.dot(1-Y,1-predictions.T))/float(Y.size)*100)
    print ("Accuracy for {} hidden units: {} %".format(n_h, accuracy))

Accuracy for 1 hidden units: 67.5 %
Accuracy for 2 hidden units: 67.25 %
Accuracy for 3 hidden units: 90.75 %
Accuracy for 4 hidden units: 90.5 %
Accuracy for 5 hidden units: 91.25 %
Accuracy for 10 hidden units: 90.25 %
Accuracy for 20 hidden units: 90.5 %

说明：

• 较大的模型（具有更多隐藏的单元）能够更好地拟合训练集，直到最终最大的模型过拟合数据为止。
• 隐藏层的最佳大小似乎在n_h = 5左右。的确，此值似乎很好地拟合了数据，而又不会引起明显的过度拟合。
• 稍后你还将学习正则化，帮助构建更大的模型（例如n_h = 50）而不会过度拟合。

总结：

• 建立具有隐藏层的完整神经网络
• 善用非线性单位
• 实现正向传播和反向传播，并训练神经网络
• 了解不同隐藏层大小（包括过度拟合）的影响。

5- 模型在其他数据集上的性能

noisy_circles, noisy_moons, blobs, gaussian_quantiles, no_structure = load_extra_datasets()
datasets = {"noisy_circles": noisy_circles,
            "noisy_moons": noisy_moons,
            "blobs": blobs,
            "gaussian_quantiles": gaussian_quantiles}

dataset = "noisy_circles"

X, Y = datasets[dataset]
X, Y = X.T, Y.reshape(1, Y.shape[0])

if dataset == "blobs":
    Y = Y%2
    
plt.scatter(X[0, :], X[1, :], c=Y.reshape(X[0,:].shape), s=40, cmap=plt.cm.Spectral);