1.4.C语言基础进阶——红黑树

C语言基础进阶——红黑树

红黑树是一类平衡二叉排序树

基本介绍

五个条件

• 每个节点非黑即红
• 根节点是黑色
• 叶节点（NIL）是黑色
  • NIL即NULL is legal
  • 是一个结点，访问是合法的
  • 在图中一般不会画出来
• 如果一个节点是红色，则它的两个子结点都是黑色的
  • 辅助控制红黑树的次要条件
• 从根节点出发到所有叶节点路径上，黑色节点数量相同
  • 控制红黑树的关键条件
  • 最长路径最多为最短路径的两倍
  • 对于红黑树的某高度下最少结点数目low(H) = low(H - 1) + low(H / 2) + 1
  • 控制了最短边和最长边的关系，整体高度增加为log(n)级别

调整策略

分为插入调整和删除调整

1. 插入调整是在祖父结点处进行调整，看它以下两层有没有出现双红情况
2. 删除调整站在父节点，看下面一层是否有双黑节点

注意以下示例中并没有画出树的所有形状，而是其中的一部分，所以一定要保证修改前后对其子树的黑色节点数量不变

插入调整

注意在插入时候，节点作为红色插入
情况一： 双红失衡，且x的叔父节点是红色的，如下两图插入所示（根据x位置不同会有4种小情况，操作同理）


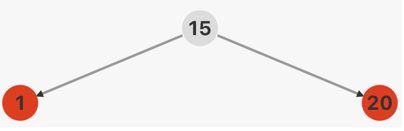
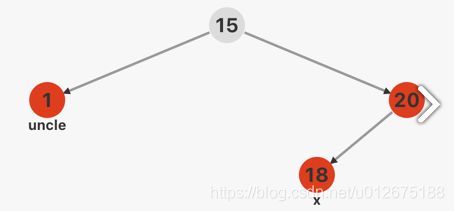
此时x祖父节点一定是黑色的，因此将祖父节点的黑色变为红色，并将x的父节点和叔父节点改为黑色，之后将x的祖父节点作为x继续向上迭代，即红色上顶

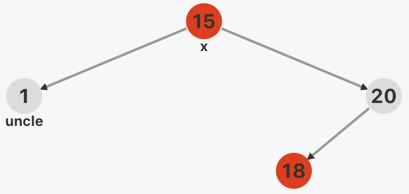
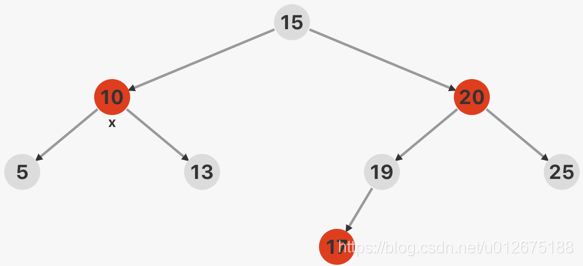
情况2： 双红失衡，且x的叔父节点为黑色，x节点在祖父节点的LL处，如下图所示（RR处类似）

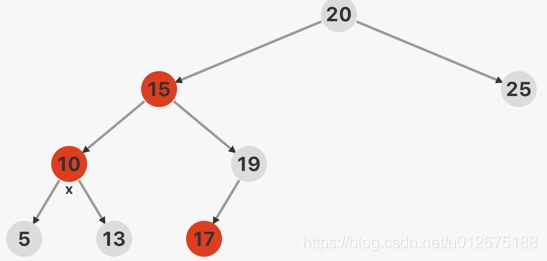
首先对15节点进行右旋操作，并分析颜色确定的节点，除17号节点之外的颜色均确定，且注意调整完后不能改变路径上黑色节点数目，类比红色上顶使用红色下沉操作，将15号节点改为黑色，20号节点改为红色，完成调整

情况3： 双红失衡，且x的叔父节点为黑色，x点在祖父节点LR处（RL处类似）

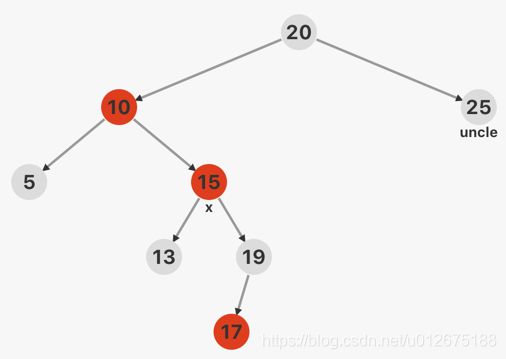
则首先对x处进行右旋操作，得到与情况2开始相同的结果，然后进行情况2操作即可

• 对红色节点进行左旋/右旋操作不会影响路径上的黑色节点数目

删除调整

红色节点不可能度为1，因为红色结点子结点必为黑色，若只有一个则不能满足条件5，同理得度为1的节点子节点一定为红色

情况1： 度为1的节点的删除，该结点一定为黑色，子结点为红色，删除后将连接上的子结点设置为黑色。

情况2： 度为0的红色结点，直接删除，没有影响

待删除结点和子结点都为黑色，首先将待删除的子结点替换到待删除节点上，标记为x，并将x的兄弟结点标记为w，此时x具有双重黑色属性，也就是说在计算路径上的黑色结点时，x要两次计数
情况3： x的兄弟节点为红色，如下图所示

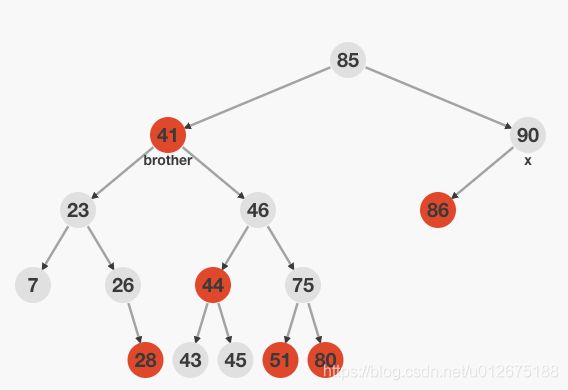
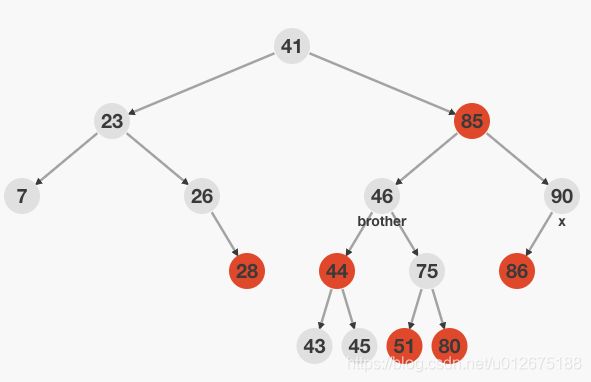
此时对兄弟结点进行右旋操作，并改变兄弟结点为黑色，父节点为红色，得到下图所示红黑树，此时x兄弟结点为黑色，按照情况4/5/6进行处理

情况4： x的兄弟结点是黑色，并且w的两个子结点为黑色

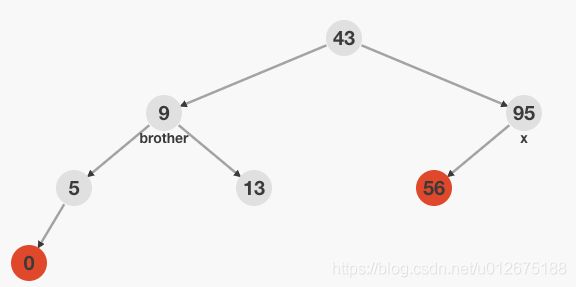
去掉x的一重黑色，并将w改为红色，在x父节点加上额外一重黑色（红色->黑色 / 黑色->双重黑色），之后将x父结点当作x，递归进行继续后续的调整操作

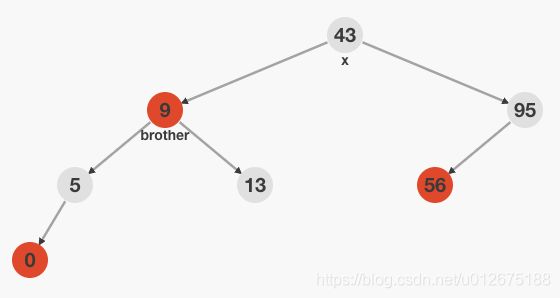
情况5： x的兄弟结点w是黑色的，w的左孩子是红色的，w的右孩子是黑色的

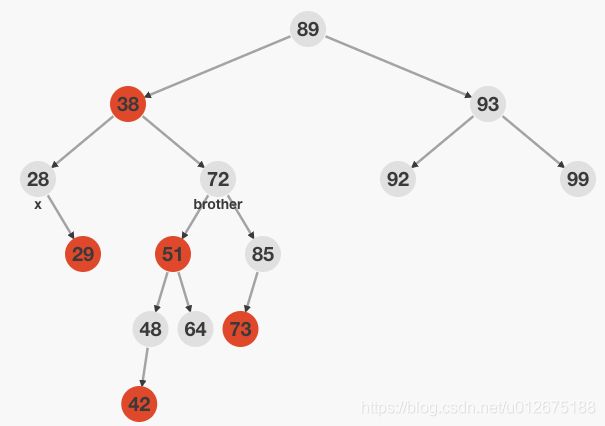
此时交换w和它的左孩子的颜色，然后对w进行右旋操作。现在w的右孩子为红色，可以按照情况6进行处理

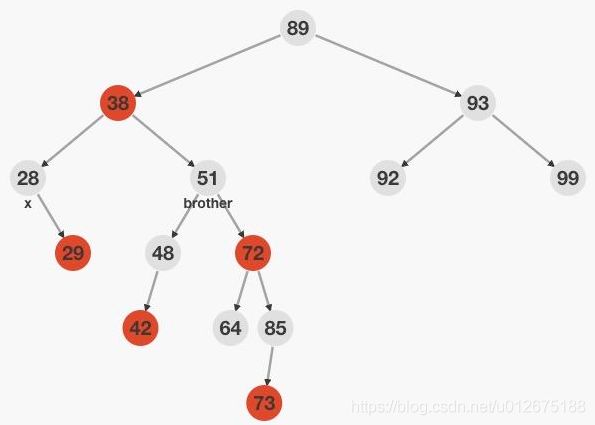
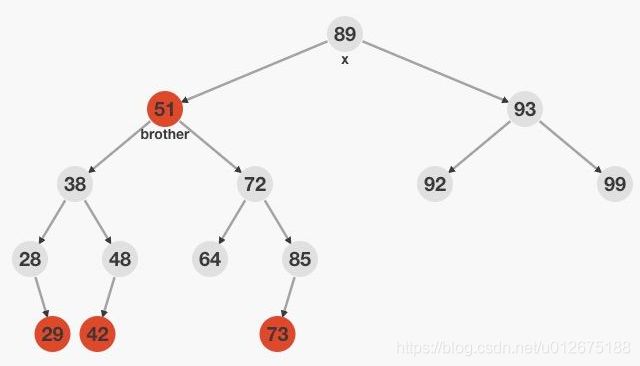
情况6： x的兄弟结点w是黑色，且w的右孩子是红色的，左孩子为红色或者黑色

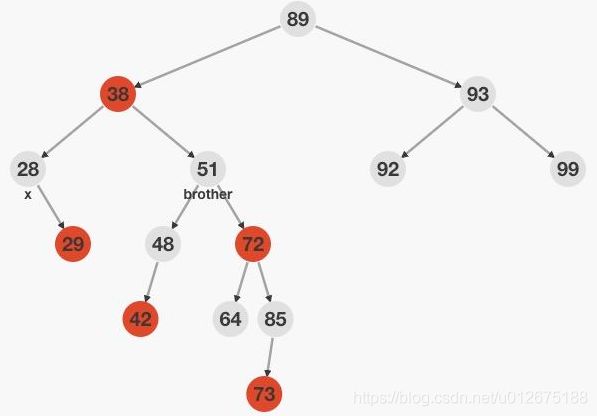
此时，调整w及其父节点和右孩子的颜色，并对w的父节点进行一次左旋，可以使x去掉一重黑色，这时以根节点作为x，继续进行判断，具体来说，51改成其父节点38颜色，38结点一定需要改成黑色

代码演示

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <string>

using namespace std;
#define L(n) (n->lchild)
#define R(n) (n->rchild)
#define K(n) (n->key)
#define C(n) (n->color)
//结构定义
typedef struct Node{
    int key;
    int color;//0 red, 1 black, 2 double black
    struct Node *lchild, *rchild;
}Node;
//虚拟空节点
Node __NIL;
#define NIL (&__NIL)
//设置函数属性在主函数之前运行
//NIL的初始化
__attribute__((constructor))
void init_NIL(){
    NIL->key = 0;
    NIL->color = 1;
    NIL->lchild = NIL->rchild = NIL;
    return ;
}
//返回一个红黑树节点
Node *getNewNode(int key){
    Node *p = (Node *)malloc(sizeof(Node));
    p->key = key;
    //默认颜色为红色
    p->color = 0;
    //程序中没有空节点，取而代之的是NIL
    p->lchild = p->rchild = NIL;
    return p;
}
//左旋
Node *left_rotate(Node *root){
    Node *temp = root->rchild;
    root->rchild = temp->lchild;
    temp->lchild = root;
    return temp;
}
//右旋
Node *right_rotate(Node *root){
    Node *temp = root->lchild;
    root->lchild = temp->rchild;
    temp->rchild = root;
    return temp;
}
//一个节点是否有红色子结点
int hasRed(Node *root){
    return C(L(root)) == 0 || C(R(root)) == 0;
}
//插入调整，返回插入之后新的根节点
Node *insert_maintain(Node *root){
    if(!hasRed(root)) return root;
    int flag = 0;
    //说明冲突在左子树发生
    if(C(L(root)) == 0 && hasRed(L(root))) flag = 1;
    //说明冲突在右子树发生
    if(C(R(root)) == 0 && hasRed(R(root))) flag = 2;
    if(flag == 0) return root;
    if(C(L(root)) == 0 && C(R(root)) == 0) goto insert_end;
    if(flag == 1){
        if(C(R(L(root))) == 0){
            root->lchild = left_rotate(root->lchild);
        }
        root = right_rotate(root);
    }else{
        if(C(L(R(root))) == 0){
            root->rchild = right_rotate(root->rchild);
        }
        root = left_rotate(root);
    }
insert_end:
    C(root) = 0;
    C(L(root)) = C(R(root)) = 1;
    return root;
}
Node *__insert(Node *root, int key){
    if(root == NIL) return getNewNode(key);
    if(key == root->key) return root;
    if(key < root->key) root->lchild = __insert(root->lchild, key);
    else root->rchild = __insert(root->rchild, key);
    //插入之后进行插入调整
    return insert_maintain(root);
}

//插入操作，返回插入之后的跟节点
Node *insert(Node *root, int key){
    root = __insert(root, key);
    root->color = 1;
    return root;
}
//返回前驱节点
Node *predecessor(Node *root){
    Node *temp = root->lchild;
    while(temp->rchild != NIL) temp = temp->rchild;
    return temp;
}
//删除调整
Node *erase_maintain(Node *root){
    //没有冲突
    if(C(L(root)) != 2 && C(R(root)) != 2) return root;
    //双黑节点的兄弟节点是红色节点
    if(hasRed(root)){
        root->color = 0;
        if(C(L(root)) == 0) {
            root = right_rotate(root);
            root->rchild = erase_maintain(root->rchild);
        }
        else {
            root = left_rotate(root);
            root->lchild = erase_maintain(root->lchild);
        }
        root->color = 1;
        return root;
    }
    //双黑节点的兄弟节点是黑色
    if(C(L(root)) ==  1){
        C(R(root)) -= 1;
        if(!hasRed(L(root))){
            C(root) += 1;
            C(L(root)) -= 1;
            return root;
        }
        if(C(L(L(root))) != 0){
            root->lchild->color = 0;
            root->lchild = left_rotate(root->lchild);
            root->lchild->color = 1;
        }
        root->lchild->color = root->color;
        root = right_rotate(root);
    }else{
        C(L(root)) -= 1;
        if(!hasRed(R(root))){
            C(root) += 1;
            C(R(root)) -= 1;
            return root;
        }
        if(C(R(R(root))) != 0){
            root->rchild->color = 0;
            root->rchild = right_rotate(root->rchild);
            root->rchild->color = 1;
        }
        root->rchild->color = root->color;
        root = left_rotate(root);
    }
    C(L(root)) = C(R(root)) = 1;
    return root;

}
Node *__erase(Node *root, int key){
    if(root == NIL) return root;
    if(key < root->key){
        root->lchild = __erase(root->lchild, key);
    }else if(key > root->key){
        root->rchild = __erase(root->rchild, key);
    }else{
        if(root->lchild == NIL || root->rchild == NIL){
            Node *temp = root->lchild == NIL ? root->rchild : root->lchild;
            temp->color += root->color;
            free(root);
            return temp;
        }else{
            Node *temp = predecessor(root);
            root->key = temp->key;
            root->lchild = __erase(root->lchild, temp->key);
        }
    }
    return erase_maintain(root);
}
//删除的入口函数
Node *erase(Node *root, int key){
    root = __erase(root, key);
    root->color = 1;
    return root;
}
//销毁操作
void clear(Node *root){
    if(root == NIL) return;
    clear(root->lchild);
    clear(root->rchild);
    free(root);
    return;
}
void output(Node *root){
    if(root == NIL) return ;
    printf("(%d : %d | %d, %d)\n", C(root), K(root), K(L(root)), K(R(root)));
    output(root->lchild);
    output(root->rchild);
    return ;
}
int main(){
    int op, val;
    Node *root = NIL;
    while(~scanf("%d%d", &op, &val)){
        switch(op){
            case 1:root = insert(root, val); break;
            case 2:root = erase(root, val); break;
        }
        printf("========= red black tree =========\n");
        output(root);
        printf("=========== end tree =============\n");
    }
    clear(root);
    return 0;
}

后记.1：

红黑树和AVL树的查询、插入、修改操作的时间复杂度是一样的，单纯查询效率上看，红黑树略慢于AVL树，但是从整体搭建上面看，红黑树的很多插入删除操作可以通过修改颜色完成，而不需要频繁进行左旋右旋操作，而左旋右旋操作时比较费时的，所以红黑树实际运行效率要比AVL更高，在很多代码中都应用到了红黑树，例如C++ STL中的set和map