ccf-csp 2015冬季真题题解

---

1. 数位之和
   问题描述
   　　给定一个十进制整数n，输出n的各位数字之和。
   输入格式
   　　输入一个整数n。
   输出格式
   　　输出一个整数，表示答案。
   样例输入
   20151220
   样例输出
   13
   样例说明
   　　20151220的各位数字之和为2+0+1+5+1+2+2+0=13。
   评测用例规模与约定
   　　所有评测用例满足：0 ≤ n ≤ 1000000000。

代码：

#include 

using namespace std;

int main(){
    int n, ans = 0;

    cin >> n;
    while(n){
        ans += n % 10;
        n /= 10;
    }
    cout << ans << endl;
    return 0;
}

---

2. 消除类游戏
   问题描述
   　　消除类游戏是深受大众欢迎的一种游戏，游戏在一个包含有n行m列的游戏棋盘上进行，棋盘的每一行每一列的方格上放着一个有颜色的棋子，当一行或一列上有连续三个或更多的相同颜色的棋子时，这些棋子都被消除。当有多处可以被消除时，这些地方的棋子将同时被消除。
   　　现在给你一个n行m列的棋盘，棋盘中的每一个方格上有一个棋子，请给出经过一次消除后的棋盘。
   　　请注意：一个棋子可能在某一行和某一列同时被消除。
   输入格式
   　　输入的第一行包含两个整数n, m，用空格分隔，分别表示棋盘的行数和列数。
   　　接下来n行，每行m个整数，用空格分隔，分别表示每一个方格中的棋子的颜色。颜色使用1至9编号。
   输出格式
   　　输出n行，每行m个整数，相邻的整数之间使用一个空格分隔，表示经过一次消除后的棋盘。如果一个方格中的棋子被消除，则对应的方格输出0，否则输出棋子的颜色编号。
   样例输入
   4 5
   2 2 3 1 2
   3 4 5 1 4
   2 3 2 1 3
   2 2 2 4 4
   样例输出
   2 2 3 0 2
   3 4 5 0 4
   2 3 2 0 3
   0 0 0 4 4
   样例说明
   　　棋盘中第4列的1和第4行的2可以被消除，其他的方格中的棋子均保留。
   样例输入
   4 5
   2 2 3 1 2
   3 1 1 1 1
   2 3 2 1 3
   2 2 3 3 3
   样例输出
   2 2 3 0 2
   3 0 0 0 0
   2 3 2 0 3
   2 2 0 0 0
   样例说明
   　　棋盘中所有的1以及最后一行的3可以被同时消除，其他的方格中的棋子均保留。
   评测用例规模与约定
   　　所有的评测用例满足：1 ≤ n, m ≤ 30。
   题解：
     模拟题，额外开一个bool数组，遍历二维矩阵，每个位置向x 和 y方向拓展，只要有一个方向拓展的节点数大于等于3就在bool数组中标记该点，之后再输出。

代码：

#include 

using namespace std;

const int MAXN = 50;
int g[MAXN][MAXN], ans[MAXN][MAXN];

int main(){
    int n, m;

    cin >> n >> m;
    for(int i = 0; i < n; i ++) 
        for(int j = 0; j < m; j ++)
            cin >> g[i][j];

    for(int i = 0; i < n; i ++)
        for(int j = 0; j < m; j ++){
        	//向x方向扩展
            int le = j, ri = j;
            while(le > 0 && g[i][le - 1] == g[i][j])
                -- le;
            while(ri < m - 1 && g[i][ri + 1] == g[i][j])
                ++ ri;
            if(ri - le + 1 >= 3){
                ans[i][j] = 1;
                continue;
            }
			//向y方向扩展
            le = i, ri = i;
            while(le > 0 && g[le - 1][j] == g[i][j])
                -- le;
            while(ri < n - 1 && g[ri + 1][j] == g[i][j])
                ++ ri;
            if(ri - le + 1 >= 3)
                ans[i][j] = 1;
        }

    for(int i = 0; i < n; i ++){
        for(int j = 0; j < m; j ++){
            if(ans[i][j])
                cout << "0 ";
            else
                cout << g[i][j] << " ";
        }
        cout << endl;
    }

    return 0;
}

---

3. 画图
   问题描述
   　　用 ASCII 字符来画图是一件有趣的事情，并形成了一门被称为 ASCII Art 的艺术。例如，下图是用 ASCII 字符画出来的 CSPRO 字样。

	..____.____..____..____...___..
　　./.___/.___||.._.\|.._.\./._.\.
　　|.|...\___.\|.|_).|.|_).|.|.|.|
　　|.|___.___).|..__/|.._.<|.|_|.|
　　.\____|____/|_|...|_|.\_\\___/.

本题要求编程实现一个用 ASCII 字符来画图的程序，支持以下两种操作：
　　画线：给出两个端点的坐标，画一条连接这两个端点的线段。简便起见题目保证要画的每条线段都是水平或者竖直的。水平线段用字符 - 来画，竖直线段用字符 | 来画。如果一条水平线段和一条竖直线段在某个位置相交，则相交位置用字符 + 代替。
　　填充：给出填充的起始位置坐标和需要填充的字符，从起始位置开始，用该字符填充相邻位置，直到遇到画布边缘或已经画好的线段。注意这里的相邻位置只需要考虑上下左右 4 个方向，如下图所示，字符 @ 只和 4 个字符 * 相邻。
　　.*.
　　*@*
　　.*.
输入格式
　　第1行有三个整数m, n和q。m和n分别表示画布的宽度和高度，以字符为单位。q表示画图操作的个数。
　　第2行至第q + 1行，每行是以下两种形式之一：
　　0 x1 y1 x2 y2：表示画线段的操作，(x1, y1)和(x2, y2)分别是线段的两端，满足要么x1 = x2 且y1 ≠ y2，要么 y1 = y2 且 x1 ≠ x2。
　　1 x y c：表示填充操作，(x, y)是起始位置，保证不会落在任何已有的线段上；c 为填充字符，是大小写字母。
　　画布的左下角是坐标为 (0, 0) 的位置，向右为x坐标增大的方向，向上为y坐标增大的方向。这q个操作按照数据给出的顺序依次执行。画布最初时所有位置都是字符 .（小数点）。
输出格式
　　输出有n行，每行m个字符，表示依次执行这q个操作后得到的画图结果。
样例输入
4 2 3
1 0 0 B
0 1 0 2 0
1 0 0 A
样例输出
AAAA
A–A
样例输入
16 13 9
0 3 1 12 1
0 12 1 12 3
0 12 3 6 3
0 6 3 6 9
0 6 9 12 9
0 12 9 12 11
0 12 11 3 11
0 3 11 3 1
1 4 2 C
样例输出

................
...+--------+...
...|CCCCCCCC|...
...|CC+-----+...
...|CC|.........
...|CC|.........
...|CC|.........
...|CC|.........
...|CC|.........
...|CC+-----+...
...|CCCCCCCC|...
...+--------+...
................

评测用例规模与约定
　　所有的评测用例满足：2 ≤ m, n ≤ 100，0 ≤ q ≤ 100，0 ≤ x < m（x表示输入数据中所有位置的x坐标），0 ≤ y < n（y表示输入数据中所有位置的y坐标）。
题解：
  注意本题的坐标系和数组坐标系不一样，需要转换一下，若本题输入的坐标为 a , b ， 则数组坐标为 n - 1 - b ， a ，使用dfs来模拟上色的过程。

代码：

#include 
#include 
#include 

using namespace std;

const int MAXN = 110;
char g[MAXN][MAXN];
bool vis[MAXN][MAXN];
int fx[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}, n, m;

void dfs(int r, int c, char ch){
    vis[r][c] = true;
    g[r][c] = ch;
    for(int i = 0; i < 4; i ++){
        int newr = r + fx[i][0];
        int newc = c + fx[i][1];
        if(newr >= 0 && newr < n && newc >= 0 && newc < m && g[newr][newc] != '|' && g[newr][newc] != '-' && g[newr][newc] != '+' && !vis[newr][newc])
            dfs(newr, newc, ch);
    }
}

int main(){
    int q, a, b, c, d;
    char ch;

    cin >> m >> n >> q;
    for(int i = 0; i < n; i ++)
        for(int j = 0; j < m; j ++)
            g[i][j] = '.';
    while(q --){
        cin >> a;
        if(a == 0){
            cin >> b >> a >> d >> c;
            //转换坐标
            a = n - 1 - a;
            c = n - 1 - c;
            //行相等
            if(a == c){
                if(b > d)
                    swap(b, d);
                for(int i = b; i <= d; i ++)
                    if(g[a][i] == '|' || g[a][i] == '+')
                        g[a][i] = '+';
                    else
                        g[a][i] = '-';
            }else{	//列相等
                if(a > c)
                    swap(a, c);
                for(int i = a; i <= c; i ++)
                    if(g[i][b] == '-'|| g[i][b] == '+')
                        g[i][b] = '+';
                    else
                        g[i][b] = '|';
            }
        }else{
            cin >> b >> a >> ch;
            a = n - 1 - a;
            memset(vis, false, sizeof(vis));
            dfs(a, b, ch);
        }
    }
    for(int i = 0; i < n; i ++){
        for(int j = 0; j < m; j ++)
            cout << g[i][j];
        cout << endl;
    }
    return 0;
}

---

4. 送货
   问题描述
   　　为了增加公司收入，F公司新开设了物流业务。由于F公司在业界的良好口碑，物流业务一开通即受到了消费者的欢迎，物流业务马上遍及了城市的每条街道。然而，F公司现在只安排了小明一个人负责所有街道的服务。
   　　任务虽然繁重，但是小明有足够的信心，他拿到了城市的地图，准备研究最好的方案。城市中有n个交叉路口，m条街道连接在这些交叉路口之间，每条街道的首尾都正好连接着一个交叉路口。除开街道的首尾端点，街道不会在其他位置与其他街道相交。每个交叉路口都至少连接着一条街道，有的交叉路口可能只连接着一条或两条街道。
   　　小明希望设计一个方案，从编号为1的交叉路口出发，每次必须沿街道去往街道另一端的路口，再从新的路口出发去往下一个路口，直到所有的街道都经过了正好一次。
   输入格式
   　　输入的第一行包含两个整数n, m，表示交叉路口的数量和街道的数量，交叉路口从1到n标号。
   　　接下来m行，每行两个整数a, b，表示和标号为a的交叉路口和标号为b的交叉路口之间有一条街道，街道是双向的，小明可以从任意一端走向另一端。两个路口之间最多有一条街道。
   输出格式
   　　如果小明可以经过每条街道正好一次，则输出一行包含m+1个整数p1, p2, p3, …, pm+1，表示小明经过的路口的顺序，相邻两个整数之间用一个空格分隔。如果有多种方案满足条件，则输出字典序最小的一种方案，即首先保证p1最小，p1最小的前提下再保证p2最小，依此类推。
   　　如果不存在方案使得小明经过每条街道正好一次，则输出一个整数-1。
   样例输入
   4 5
   1 2
   1 3
   1 4
   2 4
   3 4
   样例输出
   1 2 4 1 3 4
   样例说明
   　　城市的地图和小明的路径如下图所示。
   
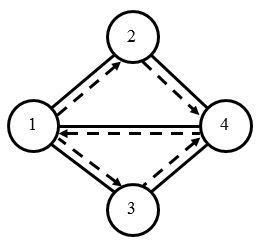
   样例输入
   4 6
   1 2
   1 3
   1 4
   2 4
   3 4
   2 3
   样例输出
   -1
   样例说明
   　　城市的地图如下图所示，不存在满足条件的路径。
   
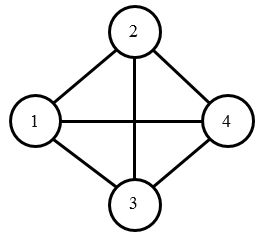
   评测用例规模与约定
   　　前30%的评测用例满足：1 ≤ n ≤ 10, n-1 ≤ m ≤ 20。
   　　前50%的评测用例满足：1 ≤ n ≤ 100, n-1 ≤ m ≤ 10000。
   　　所有评测用例满足：1 ≤ n ≤ 10000，n-1 ≤ m ≤ 100000。
   题解：
     欧拉回路模板题，使用邻接矩阵会超出空间限制，就使用邻接表来实现，还要满足字典序最小，所以使用 set g[] 数组来存储邻接表，set已经排好序了。欧拉路径要满足一下条件：

• 连通图
• 图中奇数节点个数为0 ，或者为2，而且2中的两个点分别为欧拉路径起点和终点

代码：

#include 
#include 

using namespace std;

const int MAXN = 10010;
set<int> g[MAXN];
int ans[10 * MAXN], pre[MAXN], top = 0;
//并查集判定连通性
int find(int a){
    return a == pre[a] ? a : pre[a] = find(pre[a]);
}

void dfs(int u)
{
    while (g[u].size())
    {
        int t = *g[u].begin();
        g[u].erase(t), g[t].erase(u);
        dfs(t);
    }
    ans[ ++ top] = u;
}

int main(){
    int n, m, cnt = 0, a, b;
    bool op = true;

    cin >> n >> m;
    for(int i = 1; i <= n; i ++)
        pre[i] = i;

    for(int i = 0; i < m; i ++){
        cin >> a >> b;
        g[a].insert(b);
        g[b].insert(a);
        pre[find(a)] = pre[find(b)];
    }

    for(int i = 1; i <= n; i ++){
        if(find(i) != find(1)){
            op = false;
            break;
        }   
        if(g[i].size() & 1)
            ++ cnt;
    }
    //欧拉路径判定
    if(!op || !(cnt == 0 || (cnt == 2 && g[1].size() & 1)))
        cout << -1 << endl;
    else{
        dfs(1);
        for(int i = top; i; i --)
            cout << ans[i] << " ";
    }
    return 0;
}

---

5. 矩阵
   问题描述
   　　创造一个世界只需要定义一个初状态和状态转移规则。
   　　宏观世界的物体运动规律始终跟物体当前的状态有关，也就是说只要知道物体足够多的状态信息，例如位置、速度等，我们就能知道物体之后任意时刻的状态。
   　　现在小M创造了一个简化的世界。
   　　这个世界中，时间是离散的，物理规律是线性的：世界的初始状态可以用一个m维向量b(0)表示，状态的转移方式用m×m的矩阵A表示。
   　　若已知这个世界当前的状态是b，那么下一时刻就等于b左乘状态转移矩阵A，即Ab。
   　　这个世界中，物体的状态也是离散的，也就是说可以用整数表示。再进一步，整数都可以用二进制编码拆分为有限位0和1。因此，这里的矩阵A和向量b的每个元素都是0或1，矩阵乘法中的加法运算视为异或运算（xor），乘法运算视为与运算（and）。
   　　具体地，设矩阵A第i行第j列的元素为ai, j，向量b的第i个元素为bi。那么乘法Ab所得的第k个元素为
   　　(ak,1 and b1) xor (ak,2 and b2) xor ⋯ xor (ak,m and bm)
   　　矩阵和矩阵的乘法也有类似的表达。
   　　小M发现，这样的矩阵运算也有乘法结合律，例如有A(Ab)=(AA)b=A2b。
   　　为了保证自己创造的世界维度不轻易下降，小M保证了矩阵A可逆，也就是说存在一个矩阵A-1，使得对任意向量d，都有A-1Ad=d。
   　　小M想了解自己创造的世界是否合理，他希望知道这个世界在不同时刻的状态。
   　　具体地，小M有n组询问，每组询问会给出一个非负整数k，小M希望你帮他求出Akb。
   输入格式
   　　输入第一行包含一个整数m，表示矩阵和向量的规模。
   　　接下来m行，每行包含一个长度为m的01串，表示矩阵A。
   　　接下来一行，包含一个长度为m的01串，表示初始向量b(0)。（b(0)是列向量，这里表示它的转置）
   　　注意：01串两个相邻的数字之间均没有空格。
   　　接下来一行，包含一个正整数n，表示询问的个数。
   　　最后n行，每行包含一个非负整数k，表示询问Akb(0)。
   　　注意：k可能为0，此时是求A0b(0) =b(0)。
   输出格式
   　　输出n行，每行包含一个01串，表示对应询问中Akb(0)的结果。
   　　注意：01串两个相邻的数字之间不要输出空格。
   样例输入
   3
   110
   011
   111
   101
   10
   0
   2
   3
   14
   1
   1325
   6
   124124
   151
   12312
   样例输出
   101
   010
   111
   101
   110
   010
   100
   101
   001
   100
   评测用例规模与约定
   　　本题使用10个评测用例来测试你的程序。
   　　对于评测用例1，m = 10，n = 100，k ≤ 103。
   　　对于评测用例2，m = 10，n = 100，k ≤ 104。
   　　对于评测用例3，m = 30，n = 100，k ≤ 105。
   　　对于评测用例4，m = 180，n = 100，k ≤ 105。
   　　对于评测用例5，m = 10，n = 100，k ≤ 109。
   　　对于评测用例6，m = 30，n = 100，k ≤ 109。
   　　对于评测用例7，m = 180，n = 100，k ≤ 109。
   　　对于评测用例8，m = 600，n = 100，k ≤ 109。
   　　对于评测用例9，m = 800，n = 100，k ≤ 109。
   　　对于评测用例10，m = 1000，n = 100，k ≤ 109。

贴上一道大神的70分代码，源代码：https://www.acwing.com/activity/content/code/content/886899/
代码：

#include 
#include 
#include 
#include 

using namespace std;

const int N = 1010;

int m, n;
char str[N];
bitset<1000> v[30][1000], h[30][1000], b;

void mul(int z, int x, int y)
{
    for (int i = 0; i < m; i ++ )
        for (int j = 0; j < m; j ++ )
            v[z][i][j] = h[z][j][i] = (v[x][i] & h[y][j]).count() & 1;
}

void mul(bitset<1000>& res, int x)
{
    bitset<1000> tmp;
    for (int i = 0; i < m; i ++ )
        tmp[i] = (v[x][i] & res).count() & 1;
    res = tmp;
}

void qmi(int k)
{
    bitset<1000> res = b;
    for (int i = 0; k; k >>= 1, i ++ )
        if (k & 1)
            mul(res, i);
    for (int i = 0; i < m; i ++ )
        printf("%d", !!res[i]);
    puts("");
}

int main()
{
    scanf("%d", &m);
    for (int i = 0; i < m; i ++ )
    {
        scanf("%s", str);
        for (int j = 0; j < m; j ++ )
            if (str[j] == '1')
            {
                v[0][i][j] = 1;
                h[0][j][i] = 1;
            }
    }
    scanf("%s", str);
    for (int i = 0; i < m; i ++ )
        if (str[i] == '1')
            b[i] = 1;

    for (int i = 1; i < 30; i ++ ) mul(i, i - 1, i - 1);
    scanf("%d", &n);
    while (n -- )
    {
        int k;
        scanf("%d", &k);
        qmi(k);
    }

    return 0;
}