【深度学习】锚框损失 IoU Loss、GIoU Loss、 DIoU Loss 、CIoU Loss、 CDIoU Loss、 F-EIoU Loss
文章目录
- IoU Los (Intersection over Union)
- GIoU Loss(考虑重叠面积)Generalized Intersection over Union
- DIoU Loss(考虑重叠面积,中心点距离)Distance IoU
- CIoU Loss(考虑重叠面积,中心点距离,宽高比)Complete IoU Loss
- CDIoU Loss (Control Distance IoU Loss)
- F-EIoU Loss(Focal and Efficient IOU Loss)
- 在模型上的效果评估
IoU Los (Intersection over Union)
论文:https://arxiv.org/pdf/1608.01471.pdf
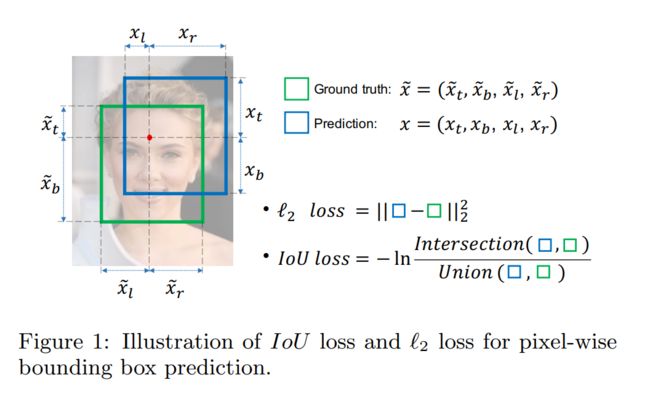
常规的Lx损失中,都是基于目标边界中的4个坐标点信息之间分别进行回归损失计算的。因此,这些边框信息之间是相互独立的。然而,直观上来看,这些边框信息之间必然是存在某种相关性的。为了解决IoU度量不可导的现象,引入了负Ln范数来间接计算IoU损失。
import numpy as np
def Iou(box1, box2, wh=False):
if wh == False:
xmin1, ymin1, xmax1, ymax1 = box1
xmin2, ymin2, xmax2, ymax2 = box2
else:
xmin1, ymin1 = int(box1[0]-box1[2]/2.0), int(box1[1]-box1[3]/2.0)
xmax1, ymax1 = int(box1[0]+box1[2]/2.0), int(box1[1]+box1[3]/2.0)
xmin2, ymin2 = int(box2[0]-box2[2]/2.0), int(box2[1]-box2[3]/2.0)
xmax2, ymax2 = int(box2[0]+box2[2]/2.0), int(box2[1]+box2[3]/2.0)
# 获取矩形框交集对应的左上角和右下角的坐标(intersection)
xx1 = np.max([xmin1, xmin2])
yy1 = np.max([ymin1, ymin2])
xx2 = np.min([xmax1, xmax2])
yy2 = np.min([ymax1, ymax2])
# 计算两个矩形框面积
area1 = (xmax1-xmin1) * (ymax1-ymin1)
area2 = (xmax2-xmin2) * (ymax2-ymin2)
inter_area = (np.max([0, xx2-xx1])) * (np.max([0, yy2-yy1])) #计算交集面积
iou = inter_area / (area1+area2-inter_area+1e-6) #计算交并比
return iou
GIoU Loss(考虑重叠面积)Generalized Intersection over Union
论文:https://arxiv.org/pdf/1902.09630.pdf
IoU Loss存在缺点:
(1)当预测框与真实框之间没有任何重叠时,IoU损失为0,梯度无法有效地反向传播和更新;
(2)IoU对重叠情况不敏感,预测框与真实框不同的重叠情况的时候,有可能计算出来的IoU是一样的;
下图展示了L1 和 L2 在很多情况表现不了anchor的回归情况,但是IoU和GIoU可以。
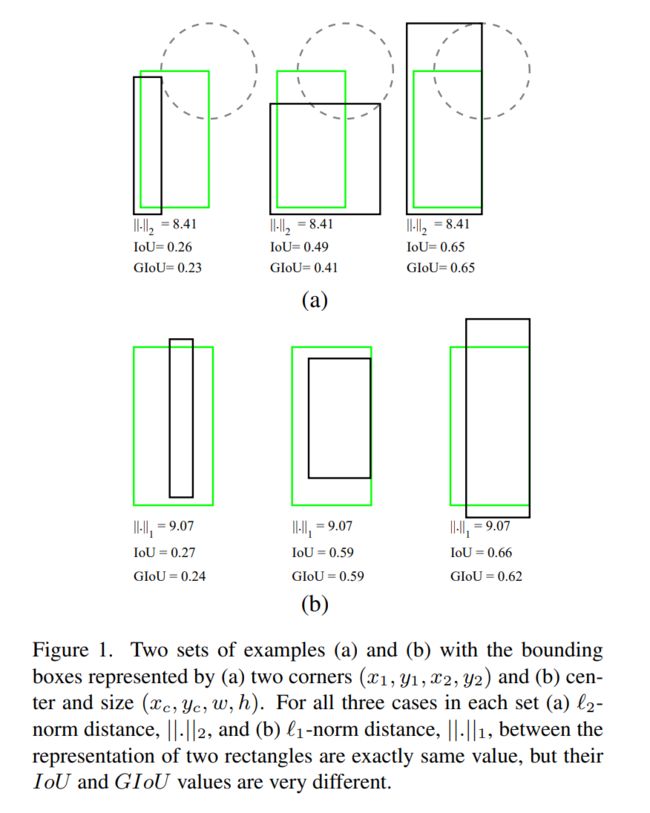
GIoU Loss(下图显示了如何计算GIoU Loss):

论文里面的C的面积是啥?通俗来说,就是同时包含了预测框和真实框的最小框的面积。
GIoU 性质:
(1) 与IoU相似,GIoU也是一种距离度量,作为损失函数的话,满足损失函数的基本要求
(2)GIoU对scale不敏感
(3)GIoU是IoU的下界,在两个框无限重合的情况下,IoU=GIoU=1
(4)IoU取值[0,1],但GIoU有对称区间,取值范围[-1,1]。在两者重合的时候取最大值1,在两者无交集且无限远的时候取最小值-1,因此GIoU是一个非常好的距离度量指标。
(5)与IoU只关注重叠区域不同,GIoU不仅关注重叠区域,还关注其他的非重合区域,能更好的反映两者的重合度。
def Giou(rec1,rec2):
#分别是第一个矩形左右上下的坐标
x1,x2,y1,y2 = rec1
x3,x4,y3,y4 = rec2
iou = Iou(rec1,rec2)
area_C = (max(x1,x2,x3,x4)-min(x1,x2,x3,x4))*(max(y1,y2,y3,y4)-min(y1,y2,y3,y4))
area_1 = (x2-x1)*(y1-y2)
area_2 = (x4-x3)*(y3-y4)
sum_area = area_1 + area_2
w1 = x2 - x1 #第一个矩形的宽
w2 = x4 - x3 #第二个矩形的宽
h1 = y1 - y2
h2 = y3 - y4
W = min(x1,x2,x3,x4)+w1+w2-max(x1,x2,x3,x4) #交叉部分的宽
H = min(y1,y2,y3,y4)+h1+h2-max(y1,y2,y3,y4) #交叉部分的高
Area = W*H #交叉的面积
add_area = sum_area - Area #两矩形并集的面积
end_area = (area_C - add_area)/area_C #闭包区域中不属于两个框的区域占闭包区域的比重
giou = iou - end_area
return giou
DIoU Loss(考虑重叠面积,中心点距离)Distance IoU
论文:https://arxiv.org/pdf/1911.08287.pdf
GIoU缺点:
(1)边框回归还不够精确
(2)收敛速度缓慢
(3)只考虑到重叠面积关系,效果不佳
DIoU性质:
(1)与GIoU loss类似,DIoU loss在与目标框不重叠时,仍然可以为边界框提供移动方向。
(2)DIoU loss可以直接最小化两个目标框的距离,因此比GIoU loss收敛快得多。
(3)对于包含两个框在水平方向和垂直方向上这种情况,DIoU损失可以使回归非常快,而GIoU损失几乎退化为IoU损失。
(4)DIoU还可以替换普通的IoU评价策略,应用于NMS中,使得NMS得到的结果更加合理和有效。
下图展示了一种特殊情况,预测框(红)包含于真实框(ground truth)中,此时GIoU退化为IoU。

论文里的第一张图往往非常重要!下图的2行展示了GIoU(第1行)和DIoU(第2行)。
黑色是初始anchor位置,绿色是target box。在第n轮的变化中,GIoU到400轮都不能很好回归,DIoU到120轮就已经完美回归到target box。

下图展示了不同方式的锚框回归效果:
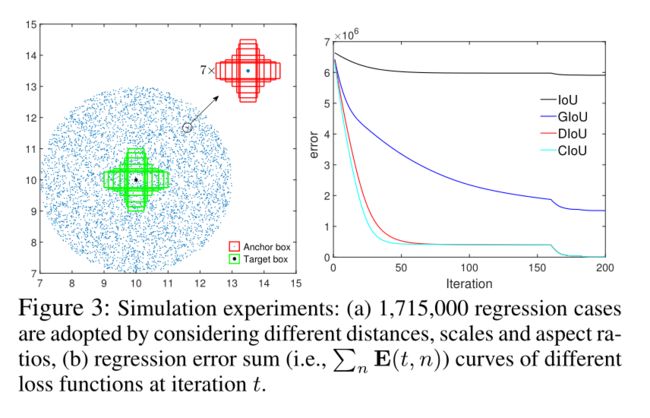
下图从数值上展示了不同锚框损失在回归时遇到的数值情况:
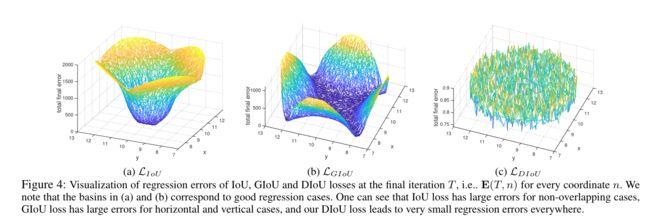
DIoU Loss: L G I o U = 1 − I o U + ∣ C − B ∪ B g t ∣ ∣ C ∣ \mathcal{L}_{G I o U}=1-I o U+\frac{\left|C-B \cup B^{g t}\right|}{|C|} LGIoU=1−IoU+∣C∣∣C−B∪Bgt∣
实现:
def Diou(bboxes1, bboxes2):
rows = bboxes1.shape[0]
cols = bboxes2.shape[0]
dious = torch.zeros((rows, cols))
if rows * cols == 0:#
return dious
exchange = False
if bboxes1.shape[0] > bboxes2.shape[0]:
bboxes1, bboxes2 = bboxes2, bboxes1
dious = torch.zeros((cols, rows))
exchange = True
# #xmin,ymin,xmax,ymax->[:,0],[:,1],[:,2],[:,3]
w1 = bboxes1[:, 2] - bboxes1[:, 0]
h1 = bboxes1[:, 3] - bboxes1[:, 1]
w2 = bboxes2[:, 2] - bboxes2[:, 0]
h2 = bboxes2[:, 3] - bboxes2[:, 1]
area1 = w1 * h1
area2 = w2 * h2
center_x1 = (bboxes1[:, 2] + bboxes1[:, 0]) / 2
center_y1 = (bboxes1[:, 3] + bboxes1[:, 1]) / 2
center_x2 = (bboxes2[:, 2] + bboxes2[:, 0]) / 2
center_y2 = (bboxes2[:, 3] + bboxes2[:, 1]) / 2
inter_max_xy = torch.min(bboxes1[:, 2:],bboxes2[:, 2:])
inter_min_xy = torch.max(bboxes1[:, :2],bboxes2[:, :2])
out_max_xy = torch.max(bboxes1[:, 2:],bboxes2[:, 2:])
out_min_xy = torch.min(bboxes1[:, :2],bboxes2[:, :2])
inter = torch.clamp((inter_max_xy - inter_min_xy), min=0)
inter_area = inter[:, 0] * inter[:, 1]
inter_diag = (center_x2 - center_x1)**2 + (center_y2 - center_y1)**2
outer = torch.clamp((out_max_xy - out_min_xy), min=0)
outer_diag = (outer[:, 0] ** 2) + (outer[:, 1] ** 2)
union = area1+area2-inter_area
dious = inter_area / union - (inter_diag) / outer_diag
dious = torch.clamp(dious,min=-1.0,max = 1.0)
if exchange:
dious = dious.T
return dious
CIoU Loss(考虑重叠面积,中心点距离,宽高比)Complete IoU Loss
被与DIoU同一篇的论文提出:https://arxiv.org/pdf/1911.08287.pdf
CIoU Loss综合考虑重叠面积(Overlap area)、中心点距离(Central point distance)和高宽比(Aspect ratio):
R C I o U = ρ 2 ( b , b g t ) c 2 + α v \mathcal{R}_{C I o U}=\frac{\rho^{2}\left(\mathbf{b}, \mathbf{b}^{g t}\right)}{c^{2}}+\alpha v RCIoU=c2ρ2(b,bgt)+αv
α \alpha α是正的权重参数(the trade-off parameter), v v v是衡量Aspect ratio的参数:
v = 4 π 2 ( arctan w g t h g t − arctan w h ) 2 v=\frac{4}{\pi^{2}}\left(\arctan \frac{w^{g t}}{h^{g t}}-\arctan \frac{w}{h}\right)^{2} v=π24(arctanhgtwgt−arctanhw)2
损失函数被定义为:
L C I o U = 1 − I o U + ρ 2 ( b , b g t ) c 2 + α v \mathcal{L}_{C I o U}=1-I o U+\frac{\rho^{2}\left(\mathbf{b}, \mathbf{b}^{g t}\right)}{c^{2}}+\alpha v LCIoU=1−IoU+c2ρ2(b,bgt)+αv
其中:
α = v ( 1 − I o U ) + v \alpha=\frac{v}{(1-I o U)+v} α=(1−IoU)+vv
实现
def bbox_overlaps_ciou(bboxes1, bboxes2):
rows = bboxes1.shape[0]
cols = bboxes2.shape[0]
cious = torch.zeros((rows, cols))
if rows * cols == 0:
return cious
exchange = False
if bboxes1.shape[0] > bboxes2.shape[0]:
bboxes1, bboxes2 = bboxes2, bboxes1
cious = torch.zeros((cols, rows))
exchange = True
w1 = bboxes1[:, 2] - bboxes1[:, 0]
h1 = bboxes1[:, 3] - bboxes1[:, 1]
w2 = bboxes2[:, 2] - bboxes2[:, 0]
h2 = bboxes2[:, 3] - bboxes2[:, 1]
area1 = w1 * h1
area2 = w2 * h2
center_x1 = (bboxes1[:, 2] + bboxes1[:, 0]) / 2
center_y1 = (bboxes1[:, 3] + bboxes1[:, 1]) / 2
center_x2 = (bboxes2[:, 2] + bboxes2[:, 0]) / 2
center_y2 = (bboxes2[:, 3] + bboxes2[:, 1]) / 2
inter_max_xy = torch.min(bboxes1[:, 2:],bboxes2[:, 2:])
inter_min_xy = torch.max(bboxes1[:, :2],bboxes2[:, :2])
out_max_xy = torch.max(bboxes1[:, 2:],bboxes2[:, 2:])
out_min_xy = torch.min(bboxes1[:, :2],bboxes2[:, :2])
inter = torch.clamp((inter_max_xy - inter_min_xy), min=0)
inter_area = inter[:, 0] * inter[:, 1]
inter_diag = (center_x2 - center_x1)**2 + (center_y2 - center_y1)**2
outer = torch.clamp((out_max_xy - out_min_xy), min=0)
outer_diag = (outer[:, 0] ** 2) + (outer[:, 1] ** 2)
union = area1+area2-inter_area
u = (inter_diag) / outer_diag
iou = inter_area / union
with torch.no_grad():
arctan = torch.atan(w2 / h2) - torch.atan(w1 / h1)
v = (4 / (math.pi ** 2)) * torch.pow((torch.atan(w2 / h2) - torch.atan(w1 / h1)), 2)
S = 1 - iou
alpha = v / (S + v)
w_temp = 2 * w1
ar = (8 / (math.pi ** 2)) * arctan * ((w1 - w_temp) * h1)
cious = iou - (u + alpha * ar)
cious = torch.clamp(cious,min=-1.0,max = 1.0)
if exchange:
cious = cious.T
return cious
CDIoU Loss (Control Distance IoU Loss)
论文:https://arxiv.org/pdf/2103.11696.pdf
F-EIoU Loss(Focal and Efficient IOU Loss)
论文:https://yfzhang114.github.io/files/cvpr_final.pdf
在模型上的效果评估
参考
https://bbs.cvmart.net/articles/4879
https://zhuanlan.zhihu.com/p/94799295
