机器学习 3.1 监督学习-线性模型(线性回归,线性分类) 学习笔记
1.模型结构
线性模型是一类有线性组合方式构成的预测性模型的统称。其基本形式如下:
f ( μ ) = a 1 a 2 + a 2 μ 2 + ⋯ + a n μ n + b f(\mu) = a_1a_2 + a_2\mu_2 + \dots + a_n\mu_n + b f(μ)=a1a2+a2μ2+⋯+anμn+b
其中, μ i \mu_i μi表示第 i i i个变量; a i a_i ai表示 μ i \mu_i μi所对应的权值参数;参数 b b b称为偏置项。
当 b ≠ 0 b \neq 0 b=0时,称上式为非齐次线性模型;当 b = 0 b = 0 b=0时,可将其化简为:
f ( μ ) = a 1 μ 1 + a 2 μ 2 + ⋯ + a n μ n f(\mu) = a_1\mu_1 + a_2\mu_2 + \dots + a_n \mu_n f(μ)=a1μ1+a2μ2+⋯+anμn
并称上式子为齐次线性模型。
显然,齐次线性模型时非齐次线性模型在 b = 0 b = 0 b=0时的情况;如果我们令 μ i = 1 \mu_i = 1 μi=1,那么非齐次线性模型也可以变为以 a n a_n an为偏置项的齐次线性模型。
可以将线性模型表示为如下的向量形式:
f ( μ ) = a T μ + b f(\mu) = a^T\mu + b f(μ)=aTμ+b
其中 a = ( a 1 , a 2 … , a n ) T a = (a_1, a_2 \dots, a_n)^T a=(a1,a2…,an)T表示权重向量; μ = ( μ 1 , μ 2 , … , μ n ) T \mu = (\mu_1, \mu_2, \dots, \mu_n)^T μ=(μ1,μ2,…,μn)T表示变量向量。
在机器学习领域,通常将样本数据表示为表征向量或特征向量形式,并默认样本数据由特征向量形式表达。具体来说,对于任意给定的一个样本 X X X,可将其表示成特征向量 ( x 1 , x 2 , … , x m ) T (x_1, x_2, \dots, x_m)^T (x1,x2,…,xm)T,即 X = ( x 1 , x 2 , … , x m ) T X = (x_1, x_2, \dots, x_m)^T X=(x1,x2,…,xm)T,每个样本数据对应各自的特征向量。此时可将线性模型表示为样本特征和权重向量的线性组合,即有:
f ( X ) = w T x + b 或 f ( X ) = w T x f(X) = w^Tx + b 或 f(X) = w^Tx f(X)=wTx+b或f(X)=wTx
其中, w = ( w 1 , w 2 , … , w m ) T w = (w_1, w_2, \dots, w_m)^T w=(w1,w2,…,wm)T为权重向量; w i w_i wi表示样本 X X X的第 i i i个特征 x i x_i xi对模型输出的影响程度。 w i w_i wi值越大,则表示特征 x i x_i xi对线性模型 f ( X ) f(X) f(X)的输出值影响就越大。
对于给定的机器学习任务,获得一个满足需求的线性模型主要通过调整线性模型的参数实现。对于参数的调整方式则有多种多样的途径和技巧。
2.线性回归
基于线性模型的回归学习任务通常称为线性回归,相应的线性模型称为线性回归模型。可以使用线性回归模型解决很多预测问题。
对于给定的样本 ξ \xi ξ,我们可以用 m m m个 x i x_i xi表示其特征,那么可以将原始样本映射称为一个 m m m元的特征向量 X = ( x 1 , x 2 , … , x m ) T X = (x_1, x_2, \dots, x_m)^T X=(x1,x2,…,xm)T。因此,我们可以将线性回归模型的初始模型表示为如下的线性组合形式:
f ( X ) = w 1 x 1 + w 2 x 2 + ⋯ + w m x m f(X) = w_1x_1 + w_2x_2 + \dots + w_m x_m f(X)=w1x1+w2x2+⋯+wmxm
其中, w = ( w 1 , w 2 , … , w m ) T w = (w_1, w_2, \dots, w_m)^T w=(w1,w2,…,wm)T为参数向量。
为了使模型的效果达到最优,我们需要对线性回归模型的参数进行不断调整优化,使其距离预测效果达到最优。在调整优化的过程中,我们需要选取适当的目标函数或损失函数作为衡量模型效果的依据。
对于给定的带标签训练样本 X X X,(通常)设其标签为 y y y,则希望线性回归模型关于该训练样本的预测输出 f ( X ) f(X) f(X)与 y y y尽可能地接近。通常采用平方误差来度量 f ( X ) f(X) f(X)和 y y y的接近程度,即 e = [ y − f ( X ) ] 2 e = [y - f(X)]^2 e=[y−f(X)]2。其中 e e e表示单个训练样本 X X X的误差。
在机器学习的模型训练中,通常使用多个训练样本。因此,对于任意给定的训练样本集 { X 1 , X 2 , … , X n } \{X_1, X_2, \dots, X_n\} {X1,X2,…,Xn}(标签为 { y 1 , y 2 , … , y n } \{y_1, y_2, \dots, y_n\} {y1,y2,…,yn}),我们将待优化的目标函数设为训练样本所产生平方误差的总和看成是模型的总误差:
J ( w ) = ∑ i = 1 n [ y i − f ( X i ) ] 2 J(w) = \sum^{n}_{i = 1}{[y_i - f(X_i)]^2} J(w)=i=1∑n[yi−f(Xi)]2
令训练样本集的特征矩阵为 A = ( X 1 , X 2 , … , X n ) T = ( x i j ) n × m A = (X_1, X_2, \dots, X_n)^T = (x_{ij})_{n \times m} A=(X1,X2,…,Xn)T=(xij)n×m。相应的训练样本标签值为 y = ( y 1 , y 2 , … , y n ) T y = (y_1, y_2, \dots, y_n)^T y=(y1,y2,…,yn)T,可将上述损失函数转化为:
J ( w ) = ( y − A w ) T ( y − A w ) J(w) = (y - Aw)^T(y - Aw) J(w)=(y−Aw)T(y−Aw)
因此,线性回归模型的构造就转化为如下最优化问题:
arg min w J ( w ) = arg min w ( y − A w ) T ( y − A w ) \arg \min_w J(w) = \arg \min_w(y - Aw)^T(y - Aw) argwminJ(w)=argwmin(y−Aw)T(y−Aw)
根据多元函数求极值的方式,我们令 J ( w ) J(w) J(w)对参数向量 w w w各分量的偏导数为 0 0 0,即:
∂ J ∂ w = A T ( y − A w ) = 0 \frac{\partial J}{\partial w} = A^T(y - Aw) = 0 ∂w∂J=AT(y−Aw)=0
展开,移项,可得:
w = ( A T A ) − 1 A T y w = (A^TA)^{-1}A^Ty w=(ATA)−1ATy
那么我们可以通过矩阵预算得出 w w w的值,并将其带入,可以得到目标线性回归模型。
上述模型存在一个非常显然的问题:可求得参数 w w w的充要条件是矩阵 A T A A^TA ATA可逆。考虑何时会出现该种情况:当矩阵 A A A的行向量之间存在线性相关关系,即不同样本之间的属性标记值存在一定的线性相关性时,矩阵 A A A不可逆,进而 A T A^T AT不可逆。由于不可逆阵相乘得到一定为不可逆阵,故矩阵 A T A A^TA ATA不可逆。
对于上述情况的解决方案,我们需要转换方式对 w w w进行计算。常见的方式有:1).岭回归 2).梯度下降法
1).岭回归
岭回归的基本思路是在现有的线性回归模型上增加一个针对 w w w的惩罚函数,通过对目标函数做正则化处理,将参数向量 w w w中所有参数的取值压缩到一个相对较小的范围,即要求 w w w中所有参数的取值不能过大,由此可以得到以下用于岭回归的损失函数:
arg min w J ( w ) = arg min w ( y − A w ) T ( y − A w ) + λ w T w \arg \min_w J(w) = \arg \min_w (y - Aw)^T(y -Aw) + \lambda w^Tw argwminJ(w)=argwmin(y−Aw)T(y−Aw)+λwTw
其中, λ ≥ 0 \lambda \geq 0 λ≥0称为正则化参数。
当 λ \lambda λ取值过大时,惩罚项 λ w T w \lambda w^Tw λwTw会对损失函数最小化产生干扰,此时优化算法会对回归模型的模型参数 w w w赋较小的值消除干扰。
同样,令 J ( w ) J(w) J(w)对参数 w w w的偏导数为 0 0 0,可得 w = ( A T A + λ I ) − 1 A T y w = (A^TA + \lambda I)^{-1}A^Ty w=(ATA+λI)−1ATy( I I I为 m m m阶单位阵)。此时,可以通过调节 λ \lambda λ保证 ( A T A + λ I ) − 1 (A^TA + \lambda I)^{-1} (ATA+λI)−1为可逆阵。
不难发现,岭回归实际上是使用了 w w w的 L 2 L^2 L2范数作为惩罚函数。
2).梯度下降
这里可以使用批量梯度下降或随机梯度下降的方式求解。我们主要关注批量梯度下降。
梯度下降算法可以用于求解多元函数极值问题,具体来说,对于函数 f ( W ) f(W) f(W),设其在某点的梯度为 g r a d f ( W ) = ▽ f ( W ) grad\ f(W) = \bigtriangledown f(W) grad f(W)=▽f(W),为一矢量,则 f ( W ) f(W) f(W)方向导数沿该方向取得最大值,即 f ( W ) f(W) f(W)沿该方向变化最快(增大)。那么在该点沿梯度负方向减小最快。我们可以从该点沿梯度方向下降一小段(即为 η \eta η,实际上我们称之为步长/学习率),到达下一个点,再沿新店的梯度反方向继续下降,如此往复求得函数极值。
根据以上策略,我们可以给函数 f ( W ) f(W) f(W)设定一个初值,然后每轮更新依次更新参数:
w i + 1 = w i − η ∂ f ( W ) ∂ w i w_{i + 1} = w_i - \eta \frac{\partial f(W)}{\partial w_i} wi+1=wi−η∂wi∂f(W)
其中 η \eta η表示步长,即学习率。
对于线性回归模型,在使用梯度下降算法进行模型求解时,一般选取平方代价函数作为损失函数:
J ( w ) = 1 2 m ∑ i = 1 m ( f ( w i ) − y i ) ) 2 J(w) = \frac{1}{2m} \sum^{m}_{i = 1}(f(w_i) - y_i))^2 J(w)=2m1i=1∑m(f(wi)−yi))2
那么我们更新参数的策略:
f o r e a c h j ( j ∈ [ 1 , n ] ) , w j + 1 = w j − η ∂ J ( W ) ∂ w j , b j + 1 = b j − η ∂ J ( W ) ∂ b for\ each\ j(j \in [1, n]),\ w_{j + 1} = w_j - \eta\frac{\partial J(W)}{\partial w_j} ,\ b_{j + 1} = b_j - \eta\frac{\partial J(W)}{\partial b} for each j(j∈[1,n]), wj+1=wj−η∂wj∂J(W), bj+1=bj−η∂b∂J(W)
其中:
∂ J ( W ) ∂ w j = ∂ ∂ w j 1 2 m ∑ i = 1 m ( f ( x i ) − y i ) ) 2 = 1 m ∑ i = 1 m ( f ( w i ) − y i ) x i \frac{\partial J(W)}{\partial w_j} = \frac{\partial}{\partial w_j} \frac{1}{2m} \sum^{m}_{i = 1}(f(x_i) - y_i))^2 = \frac1m \sum_{i = 1}^{m}(f(w_i) - y_i)x_i ∂wj∂J(W)=∂wj∂2m1i=1∑m(f(xi)−yi))2=m1i=1∑m(f(wi)−yi)xi
类似的,对于偏置项 b b b的更新,可以将 b b b看作 w 0 w_0 w0,对应项 x 0 = 1 x_0 = 1 x0=1,则:
∂ J ( W ) ∂ b = ∂ J ( W ) ∂ w 0 = ∂ ∂ w 0 1 2 m ∑ i = 1 m ( f ( x i ) − y i ) ) 2 = 1 m ∑ i = 1 m ( f ( w i ) − y i ) \frac{\partial J(W)}{\partial b} = \frac{\partial J(W)}{\partial w_0} = \frac{\partial}{\partial w_0} \frac{1}{2m} \sum^{m}_{i = 1}(f(x_i) - y_i))^2 = \frac1m \sum_{i = 1}^{m}(f(w_i) - y_i) ∂b∂J(W)=∂w0∂J(W)=∂w0∂2m1i=1∑m(f(xi)−yi))2=m1i=1∑m(f(wi)−yi)
那么我们可以得到每轮梯度下降更新参数的方法:
w j + 1 = w j − η 1 m ∑ i = 1 m ( f ( w i ) − y i ) x i , b j + 1 = b j − η 1 m ∑ i = 1 m ( f ( w i ) − y i ) w_{j + 1} = w_j - \eta\frac1m \sum_{i = 1}^{m}(f(w_i) - y_i)x_i ,\\ b_{j + 1} = b_j - \eta\frac1m \sum_{i = 1}^{m}(f(w_i) - y_i) wj+1=wj−ηm1i=1∑m(f(wi)−yi)xi,bj+1=bj−ηm1i=1∑m(f(wi)−yi)
值得注意的是,由于梯度下降求得的是局部最小值,因此需要随机初始化不同的参数进行训练,选取拟合效果最好的最为最终模型。
使用Python实现的批量梯度下降算法如下所示。
import numpy as np
import matplotlib.pyplot as plt
def loadData(strr):
x, y = [], []
with open(strr, 'r') as file:
x = list(map(float, file.readline().strip().split(' ')))
y = list(map(float, file.readline().strip().split(' ')))
return x, y
class LinearRegression(object):
def __init__(self, dimension):
self.w = [0 for i in range(dimension)]
self.b = 0
self.dimension = dimension
def step_regression(self, xSet, ySet, rate):
x, y, N = np.array(xSet), np.array(ySet), len(xSet)
samples = zip(x, y)
mGradient = np.array([0.0 for i in range(self.dimension)])
biasGradient = 0.0
for [nx, ny] in samples:
mGradient += (1 / N) * ((np.dot(self.w, nx.T) + self.b) - ny) * nx
biasGradient += (1 / N) * ((np.dot(self.w, nx.T) + self.b) - ny)
self.w = self.w - rate * mGradient
self.b = self.b - rate * biasGradient
def getParameters(self):
return self.w, self.b
if __name__ == "__main__":
x, y = loadData(r"./data.TXT")
nlg = LinearRegression(1)
for i in range(100000):
nlg.step_regression(x, y, 0.0001)
w, b = nlg.getParameters()
print(w, b)
plt.scatter(x, y, color = 'red')
x = np.arange(50)
y = w * x + b
plt.plot(x, y, color = 'blue')
plt.show()
其中data如下所示:
0.7175 1.1334 2.4458 3.5088 4.5305 5.8597 6.6777 7.8058 8.5312 9.9559 10.0667 11.5415 12.2817 13.4809 14.6849 15.2083 16.6082 17.3262 18.8808 19.1334 20.1024 21.9591 22.1529 23.1525 24.1556 25.0896 26.4544 27.6689 28.8313 29.7902 30.7127 31.4726 32.7086 33.9581 34.5058 35.3051 36.7898 37.2364 38.2343 39.4647 40.6194 41.6153 42.1226 43.1238 44.2845 45.7357 46.4113 47.8290 48.9351 49.3991
166.8556 159.4011 168.1423 201.9823 265.0215 164.3088 184.0195 309.0621 241.7049 269.2471 345.3295 320.4802 346.2132 300.7559 309.9974 326.6441 355.9061 365.9207 401.6982 388.4757 397.3731 485.4321 388.4500 467.7333 528.6302 490.2403 449.5324 504.3822 494.4272 603.7605 537.4864 523.1190 584.7927 579.5038 573.9685 582.5431 626.8837 557.5200 603.1097 662.3925 641.9709 660.9893 705.6632 762.4351 687.1629 804.3925 769.3359 714.7646 783.8658 793.7925
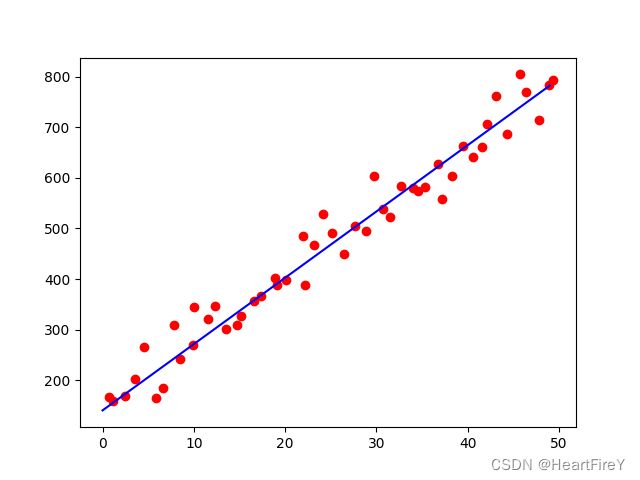
在学习率 η = 0.0001 \eta = 0.0001 η=0.0001,迭代轮数 100000 100000 100000次时,可以得到如下所示的结果:
可以自行设置训练数据和测试数据,测试模型效果。
批量梯度下降法是对所有的样本求梯度,当数据规模很大的时候,整个计算过程是很耗时的。有一种办法,每次只对一个样本求梯度,或者每次只对若干个样本求梯度,这种方法就叫做随机梯度下降法 。在大部分场景下,随机梯度下降的时间和效果要优于批量梯度下降。
3.线性分类
如果回归模型输出的值为连续值,显然时难以实现分类的效果的。而如果输出的值为离散值,则容易进行分类。因此,一个比较基本的思路是:将线性模型的输出值(连续值)进行离散化,就可以将对应的线性回归模型改造为线性分类模型。我们称之为线性分类问题,模型即线性分类器。
如何将连续值进行离散化?我们可以将线性模型输出值的取值范围划分为有限个不相交的区间,每个区间表示一个类别,从而实现离散化。我们常用阶跃函数作为激活函数对输出进行离散化。但阶跃函数并不是连续函数,因此我们需要设计一些连续可导函数作为激活函数对输出进行离散化:
3.1 激活函数
3.1.1 Sigmoid函数
Sigmoid 是常用的非线性的激活函数,表达式如下:
f ( x ) = 1 1 + e − x f(x) = \frac{1}{1 + e^{-x}} f(x)=1+e−x1
- 特性:它能够把输入的连续实值变换为 0 0 0和 1 1 1之间的输出,特别的,如果是非常大的负数,那么输出就是 0 0 0;如果是非常大的正数,输出就是 1 1 1.
- 缺点:在深度神经网络中梯度反向传递时导致梯度爆炸和梯度消失,其中梯度爆炸发生的概率非常小,而梯度消失发生的概率比较大。
3.1.2 tanh函数
tanh函数也是非线性函数,其函数解析式为:
t a n h ( x ) = e x − e − x e x + e − x tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} tanh(x)=ex+e−xex−e−x
tanh读作Hyperbolic Tangent,它解决了Sigmoid函数的不是zero-centered输出问题,然而,梯度消失(gradient vanishing)的问题和幂运算的问题仍然存在。
3.1.3 Relu函数
Relu函数实际上就是个取最大值函数,其函数解析式如下所示:
f ( x ) = max ( 0 , x ) f(x) = \max{(0, x)} f(x)=max(0,x)
Relu是目前最常用的激活函数,一般搭建人工神经网络时推荐优先尝试Relu并非全区间可导,但我们可以取sub-gradient-
- 解决了
gradient vanishing问题 (在正区间) - 计算速度非常快,只需要判断输入是否大于 0 0 0
- 收敛速度远快于
Sigmoid和tanh
- 解决了
-
ReLU的输出不是zero-centeredDead ReLU Problem,指的是某些神经元可能永远不会被激活,导致相应的参数永远不能被更新。有两个主要原因可能导致这种情况产生: (1) 非常不幸的参数初始化,这种情况比较少见 (2)learning rate太高导致在训练过程中参数更新太大,不幸使网络进入这种状态。解决方法是可以采用Xavier初始化方法,以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。
3.1.4 Leaky ReLU函数(PReLU)
函数表达式:
f ( x ) = max ( α x , x ) f(x) = \max(\alpha x, x) f(x)=max(αx,x)
人们为了解决Dead ReLU Problem,提出了将ReLU的前半段设为 α x \alpha x αx而非 0 0 0,通常 α = 0.01 \alpha=0.01 α=0.01。另外一种直观的想法是基于参数的方法,即 P a r a m e t r i c R e L U : f ( x ) = max ( α x , x ) Parametric ReLU:f(x) = \max(\alpha x, x) ParametricReLU:f(x)=max(αx,x),其中 α \alpha α
可由方向传播算法学出来。理论上来讲,Leaky ReLU有ReLU的所有优点,外加不会有Dead ReLU问题,但是在实际操作当中,并没有完全证明Leaky ReLU总是好于ReLU。
1.5 ELU(Exponential Linear Units) 函数
函数表达式:
f ( x ) = { x , i f x > 0 α ( e x − 1 ) , o t h e r w i s e f(x) = \left\{\begin{matrix} x ,&if\ x > 0\\ \alpha(e^x - 1), &otherwise \end{matrix}\right. f(x)={x,α(ex−1),if x>0otherwise
ELU不会有Dead ReLU问题 输出的均值接近 0 0 0,zero-centered。但计算量偏大,在目前的实际应用中并未被证明总是好于ReLU。
3.2 线性分类器
我们可以使用简单的神经网络-感知机模型实现线性分类器的功能,具体见:神经网络1.1 感知机模型(神经元模型)
在感知机中,我们常用 S i g m o i d Sigmoid Sigmoid函数作为激活函数:
g ( x ) = 1 1 + e − x g(x) = \frac{1}{1 + e^{-x}} g(x)=1+e−x1
对其求导数:
g ′ ( x ) = g ( x ) [ 1 − g ( x ) ] g'(x) = g(x)[1 - g(x)] g′(x)=g(x)[1−g(x)]
设线性回归模型 f ( X ) = w T X f(X) = w^TX f(X)=wTX,带入 S i g m o i d Sigmoid Sigmoid函数:
g ( f ( X ) ) = 1 1 + e − w T X g(f(X)) = \frac{1}{1 + e^{-w^TX}} g(f(X))=1+e−wTX1
令 H ( X ) = 1 1 + e − w T X H(X) = \frac{1}{1 + e^{-w^TX}} H(X)=1+e−wTX1,则 H ( X ) ∈ ( 0 , 1 ) H(X) \in (0, 1) H(X)∈(0,1),可以将其看作关于 X X X的概率分布: H ( X ) H(X) H(X)越接近 1 1 1,则 X X X属于正例的可能性越大,反之属于正例概率越小。也就是说, H ( X ) H(X) H(X)为样本 X X X在正例条件下 f ( x ) = 1 f(x) = 1 f(x)=1的后验概率:
P ( f ( X ) = 1 ∣ X ) = H ( X ) P(f(X) = 1|X) = H(X) P(f(X)=1∣X)=H(X)
在实际过程中,对于数据集 D = X i , y i D = {X_i, y_i} D=Xi,yi,如果 X i X_i Xi为正例,我们希望 P ( y i = 1 ∣ X i , w ) = H ( X ) P(y_i = 1|X_i, w) = H(X) P(yi=1∣Xi,w)=H(X)尽可能大;如果 X X X为反例,我们希望 P ( y i = 0 ∣ X i ; w ) = 1 − P ( y i = 1 ∣ X i ; w ) = 1 − H ( X ) P(y_i = 0|X_i; w) = 1 - P(y_i = 1|X_i; w) = 1 - H(X) P(yi=0∣Xi;w)=1−P(yi=1∣Xi;w)=1−H(X)越大越好。我们可以使用极大似然估计的方法对似然函数进行最优化计算,获得优化模型的参数向量 w w w。
我们首先对联合概率分布:
P ( y i ∣ X i ; w ) = H ( X i ) y i [ 1 − H ( X i ) ] ( 1 − y i ) P(y_i|X_i; w) = H(X_i)^{y_i}[1 - H(X_i)]^{(1 - y_i)} P(yi∣Xi;w)=H(Xi)yi[1−H(Xi)](1−yi)
此时,我们希望联合概率分布的值越大越好,那么可得似然函数:
l = ∏ i P ( y i ∣ X i ; w ) = ∏ i H ( X i ) y i [ 1 − H ( X i ) ] ( 1 − y i ) l = \prod_i P(y_i | X_i; w) = \prod_i H(X_i)^{y_i}[1 - H(X_i)]^{(1 - y_i)} l=i∏P(yi∣Xi;w)=i∏H(Xi)yi[1−H(Xi)](1−yi)
对两边同时取对数,可得:
L = − ln l = ∑ i = 1 n [ y i ln H ( X i ) + ( 1 − y i ) ln ( 1 − H ( X i ) ) ] L = -\ln l = \sum_{i = 1}^{n}[y_i\ln H(X_i)+(1 - y_i)\ln(1 - H(X_i))] L=−lnl=i=1∑n[yilnH(Xi)+(1−yi)ln(1−H(Xi))]
可将以上函数作为目标函数,求解最优化问题:
w = arg max w { ∑ i = 1 n [ y i ln H ( X i ) + ( 1 − y i ) ln ( 1 − H ( X i ) ) ] } w = \arg \max_w \{\sum_{i = 1}^{n}[y_i\ln H(X_i)+(1 - y_i)\ln(1 - H(X_i))]\} w=argwmax{i=1∑n[yilnH(Xi)+(1−yi)ln(1−H(Xi))]}
3.3 线性判别分析
线性判别分析(Linear Discriminant Analysis, LDA),又称Fisher判别分析(FLD)。该方法也是构造一种线性分类器,用于实现机器学习分类任务。
线性判别分析的基本思想是在特征空间中寻找一个合适的投影轴或投影直线,并将样本的特征向量投影到该投影直线,使得样本在该投影直线上更易于分类。具体的来说,对于给定的训练样本集,我们可以设法将训练样本投影到一种具有合适方向的直线 f ( x ) = w T x f(x) = w^Tx f(x)=wTx上,使得该直线上同类样例的投影点尽可能的接近,而异类的投影点尽可能远离。这样在进行分类的时候,可以将其投影到该直线上并根据投影点的位置来确定其类别。
由于不同的投影点之间会产生不同的投影效果,故投影直线方向的选取是线性判别模型的分析的关键。
假设存在[二分类]问题,给定数据集 D = { X i , y i } i = 1 n , y i = { 0 , 1 } D = \{X_i, y_i\}^{n}_{i = 1}, y_i = \{0, 1\} D={Xi,yi}i=1n,yi={0,1},设其中 X i k ( k = 1 , 2 , … , n 1 ) X_{ik}(k = 1, 2,\dots, n_1) Xik(k=1,2,…,n1)为第一类样本点, X i t ( t = 1 , 2 , … , n 2 ) X_{it}(t = 1, 2, \dots, n_2) Xit(t=1,2,…,n2)为第二类样本点。我们分别对这两类样本点在投影直线上的投影求中心值 μ 1 , μ 2 \mu_1, \mu_2 μ1,μ2:
μ ˉ 1 = 1 n 1 ∑ i = 1 n 1 w T X i k = w T X ˉ 1 μ ˉ 2 = 1 n 2 ∑ i = 1 n 2 w T X i t = w T X ˉ 2 \bar \mu_1 = \frac{1}{n_1} \sum^{n_1}_{i = 1}{w^TX_{ik}} = w^T\bar X_1 \\ \bar \mu_2 = \frac{1}{n_2} \sum^{n_2}_{i = 1}{w^TX_{it}} = w^T\bar X_2 \\ μˉ1=n11i=1∑n1wTXik=wTXˉ1μˉ2=n21i=1∑n2wTXit=wTXˉ2
令 L ( w ) = ∣ μ 1 − μ 2 ∣ = ∣ w T ( X ˉ 1 − X ˉ 2 ) ∣ L(w) = |\mu_1 - \mu_2| = |w^T(\bar X_1 - \bar X_2)| L(w)=∣μ1−μ2∣=∣wT(Xˉ1−Xˉ2)∣,我们的第一个目标为:使两类样本中心点的位置尽可能的远离。
对于同类样本,我们使用该类样本的散列值表示他们在投影直线 f ( X ) = w T X f(X) = w^TX f(X)=wTX上的离散程度。所谓某类样本的散列值,就是用该类所有样本在该投影直线上投影值与该类所有样本在该直线上平均投影值之间的平方误差之和。
令 s 1 − 2 \overset{-2}{s_1} s1−2和 s 1 − 2 \overset{-2}{s_1} s1−2分别表示两类样本投影到直线 f ( X ) = w T X f(X) = w^TX f(X)=wTX后的散列值,则:
s 1 − 2 = ∑ k = 1 n 1 ( w T X i k − μ 1 ‾ ) 2 s 2 − 2 = ∑ k = 1 n 2 ( w T X i t − μ 2 ‾ ) 2 \overset{-2}{s_1} = \sum^{n_1}_{k = 1}(w^TX_{ik} - \overline{\mu_1})^2\\ \overset{-2}{s_2} = \sum^{n_2}_{k = 1}(w^TX_{it} - \overline{\mu_2})^2 s1−2=k=1∑n1(wTXik−μ1)2s2−2=k=1∑n2(wTXit−μ2)2
散列值可以用于形容样本在投影直线上投影点分布的密集程度,其值越大,则分布越稀松,反之则密集。对于线性判别问题,我们的目标是类内距离最小化,令 S ( w ) = s 1 − 2 + s 1 − 2 S(w) = \overset{-2}{s_1}+\overset{-2}{s_1} S(w)=s1−2+s1−2,则我们希望 S ( w ) S(w) S(w)的值尽可能地小。
综上所述,我们将类内距离最小化,类间距离最大化描述为:我们希望 L ( w ) L(w) L(w)的值尽可能大,而 S ( w ) S(w) S(w)值尽可能小。因此可以构造目标函数:
J ( w ) = L ( w ) 2 S ( w ) = ∣ μ 1 − μ 2 ∣ 2 s 1 − 2 + s 1 − 2 J(w) = \frac{L(w)^2}{S(w)} = \frac{|\mu_1 - \mu_2|^2}{\overset{-2}{s_1}+\overset{-2}{s_1}} J(w)=S(w)L(w)2=s1−2+s1−2∣μ1−μ2∣2
学习目标为寻找 J ( w ) J(w) J(w)值最大的参数向量 w w w,并将其作为投影直线 f ( X ) = w T X f(X) = w^TX f(X)=wTX的参数。
首先,考察 J ( w ) J(w) J(w)的分子: ( μ ˉ 1 − μ ˉ 2 ) 2 = [ w T ( X ˉ 1 − X ˉ 2 ) ] 2 = ( w T X 1 − w T X 2 ) 2 = w T ( X ˉ 1 − X ˉ 2 ) ( X ˉ 1 − X ˉ 2 ) T w (\bar \mu_1 - \bar \mu_2)^2 = [w^T(\bar X_1 - \bar X_2)]^2 = (w^TX_1 - w^TX_2)^2 = w^T(\bar X_1 - \bar X_2)(\bar X_1 - \bar X_2)^Tw (μˉ1−μˉ2)2=[wT(Xˉ1−Xˉ2)]2=(wTX1−wTX2)2=wT(Xˉ1−Xˉ2)(Xˉ1−Xˉ2)Tw
其中 S b = ( X ˉ 1 − X ˉ 2 ) ( X ˉ 1 − X ˉ 2 ) T S_b = (\bar X_1 - \bar X_2)(\bar X_1 - \bar X_2)^T Sb=(Xˉ1−Xˉ2)(Xˉ1−Xˉ2)T称为类间散度矩阵。
再考察 J ( w ) J(w) J(w)的分母:
s 1 − 2 = ∑ k = 1 n 1 ( w T X i k − μ 1 ‾ ) 2 = ∑ k = 1 n 1 ( w T X i k − w T X ˉ 1 ) 2 = ∑ k = 1 n 1 w T ( x i k − X ˉ 1 ) ( x i k − X ˉ 1 ) T w = w T S 1 w \overset{-2}{s_1} = \sum^{n_1}_{k = 1}(w^TX_{ik} - \overline{\mu_1})^2 = \sum^{n_1}_{k = 1}(w^TX_{ik} - w^T\bar X_1)^2 = \sum^{n_1}_{k = 1}w^T(x_{ik} - \bar X_1)(x_{ik} - \bar X_1)^Tw = w^TS_1w s1−2=k=1∑n1(wTXik−μ1)2=k=1∑n1(wTXik−wTXˉ1)2=k=1∑n1wT(xik−Xˉ1)(xik−Xˉ1)Tw=wTS1w
(令 S 1 = ( x i k − X ˉ 1 ) ( x i k − X ˉ 1 ) T S_1 = (x_{ik} - \bar X_1)(x_{ik} - \bar X_1)^T S1=(xik−Xˉ1)(xik−Xˉ1)T)
同理,可得 s 1 − 2 = w T S 2 w \overset{-2}{s_1} = w^TS_2w s1−2=wTS2w。我们将 S w = S 1 + S 2 S_w = S_1 + S_2 Sw=S1+S2称为类内散度矩阵。则原目标函数转变为:
J ( w ) = w T S b w w T S w w J(w) = \frac{w^TS_bw}{w^TS_ww} J(w)=wTSwwwTSbw
在对目标函数求最大值前,需要对分母进行归一化处理,即使 ∣ w T S w w ∣ = 1 |w^TS_ww| = 1 ∣wTSww∣=1,则求 J ( w ) J(w) J(w)最大值等价于求解以下条件极值:
min w T S b w ; s . t . w T S w w = 1 \min w^TS_bw; s.t. w^TS_ww = 1 minwTSbw;s.t.wTSww=1
引入拉格朗日乘数项, C ( w ) = w T S b w − λ ( w T S w w − 1 ) C(w) = w^TS_bw - \lambda(w^TS_ww - 1) C(w)=wTSbw−λ(wTSww−1), 并令 C ( w ) C(w) C(w)对 w w w的导数为零,可得
d C d w = 2 S b w − 2 λ S w w = 0 \frac{d C}{d w} = 2S_bw - 2\lambda S_ww = 0 dwdC=2Sbw−2λSww=0
故: S b w = λ S w w S_bw = \lambda S_ww Sbw=λSww。如果 S w S_w Sw可逆,则有 S w − 1 S b w = λ w S_w^{-1}S_bw = \lambda w Sw−1Sbw=λw。
不难看出, w w w是矩阵 S w − 1 S b S_w^{-1}S_b Sw−1Sb的特征向量,代入 S b = ( X ˉ 1 − X ˉ 2 ) ( X ˉ 1 − X ˉ 2 ) T S_b = (\bar X_1 - \bar X_2)(\bar X_1 - \bar X_2)^T Sb=(Xˉ1−Xˉ2)(Xˉ1−Xˉ2)T,令常数 λ w = ( X ˉ 1 − X ˉ 2 ) T w \lambda_w = (\bar X_1 - \bar X_2)^Tw λw=(Xˉ1−Xˉ2)Tw,则:
S b w = ( X ˉ 1 − X ˉ 2 ) λ w S_bw = (\bar X_1 - \bar X_2)\lambda_w Sbw=(Xˉ1−Xˉ2)λw
因此:
S w − 1 S b w = S w − 1 ( X ˉ 1 − X ˉ 2 ) λ w = λ w S_w^{-1}S_bw = S_w^{-1}(\bar X_1 - \bar X_2)\lambda_w = \lambda w Sw−1Sbw=Sw−1(Xˉ1−Xˉ2)λw=λw
由于对 w w w伸缩任何倍数被都不会改变投影方向,因此略去常数 λ , λ w \lambda,\lambda_w λ,λw,可得:
w = S w − 1 ( X ˉ 1 − X ˉ 2 ) w = S_w^{-1}(\bar X_1 - \bar X_2) w=Sw−1(Xˉ1−Xˉ2)
至此,我们只需要求得训练样本的均值和列内散度矩阵,即可获得最佳投影直线。
不难发现,LDA实际上是将高维数据进行降维操作的一种方式,即通过将高维数据映射到低维超平面上,从而实现降维效果。因此线性判别分析还可以应用于数据降维实现的数据特征提取等方面。