CART决策树----基尼指数划分

CART决策树----基尼指数划分

一.决策树算法的构建

一般的，一棵决策树包含一个根节点，若干个内部结点和若干个叶结点；叶结点对应于决策结果，其他每个结点则对应于一个属性测试；每个结点包含的样本集合根据测试属性的结果被划分到子结点中；根节点包含样本全集。从根节点到每个叶节点的路径对应了一个判定测试序列。决策树学习的目的是为了产生一棵泛化能力强，即处理未见例能力强的决策树，其基本流程遵循简单而直观的分而治之策略
————from 西瓜书

决策树算法伪代码：
决策树的生成是一个递归的过程，在决策树生成算法的过程中，有三种情形需要递归返回：

• （1）当前结点包含的样本全部属于同一类别，无需划分，例如当前结点全是正例（好瓜）：设置为叶子结点，返回当前集合的类别
• （2）当前属性集为空，或是所有样本在所有属性上取值相同，无法划分，例如对所有类别属性的划分都已经结束，无法进一步划分，或者比如色泽青绿的瓜其他属性都一样，也不必继续划分。：把当前结点标记为叶子结点，并将其类别设置为该节点所含样本最多的类别。
• （3）当前结点包含的样本集合为空，不能划分：当前结点设置为叶子节点，单将其类别设置为父节点所含样本中最多的类别。

二.划分选择——基尼指数

在决策树的建立过程当中，涉及到很多对当前结点集合的划分操作，而如何选择最优划分属性是决策树算法的关键问题之一。
一般而言，随着划分过程的不断进行，我们希望决策树的分支节点所包含的样本尽可能属于同一类别，即结点的 纯度（purity） 越来越高。

基尼指数：CART决策树使用基尼指数（Gini index）来选择划分属性：
$$Gini(D)=1-\sum _{k=1}^{|y|}{p_k}^2$$
直观来说，Gini（D）反映了从数据集D中随机抽取两个样本，其类别标记不一致的概率，因此Gini（D）越小，则数据集D的纯度越高。
属性a的基尼指数定义为：
$$Gini\_index(D,a)=\sum _{v=1}^V\frac{|D^v|}{|D|}Gini(D^v)$$
于是在候选属性集A中，选择哪个使得划分后基尼指数最小的属性作为最优划分属性，即：
$$a\ast =argminGini\_index(D,a)$$

西瓜数据集如下：

编号	色泽	根蒂	敲声	纹理	脐部	触感	好瓜
0	青绿	蜷缩	浊响	清晰	凹陷	硬滑	是
1	乌黑	蜷缩	沉闷	清晰	凹陷	硬滑	是
2	乌黑	蜷缩	浊响	清晰	凹陷	硬滑	是
3	青绿	蜷缩	沉闷	清晰	凹陷	硬滑	是
4	浅白	蜷缩	浊响	清晰	凹陷	硬滑	是
5	青绿	稍蜷	浊响	清晰	稍凹	软粘	是
6	乌黑	稍蜷	浊响	稍糊	稍凹	软粘	是
7	乌黑	稍蜷	浊响	清晰	稍凹	硬滑	否
8	乌黑	稍蜷	沉闷	稍糊	稍凹	硬滑	否
9	青绿	硬挺	清脆	清晰	平坦	软粘	否
10	浅白	硬挺	清脆	模糊	平坦	硬滑	否
11	浅白	蜷缩	浊响	模糊	平坦	软粘	否
12	青绿	稍蜷	浊响	稍糊	凹陷	硬滑	否
13	浅白	稍蜷	沉闷	稍糊	凹陷	硬滑	否
14	乌黑	稍蜷	浊响	清晰	稍凹	软粘	否
15	浅白	蜷缩	浊响	模糊	平坦	硬滑	否
16	青绿	蜷缩	沉闷	稍糊	稍凹	硬滑	否

我们来模拟一下第一次根据基尼指数选择最后划分属性的过程：
假如我们选择的训练集为以下编号的数据：
[0, 1, 2, 3, 5, 6, 9, 13, 14, 15, 16]
我们以对色泽的基尼指数计算为例：
色泽属性中对应的特征有：青绿，乌黑，浅白
在训练集中：

• 青绿的个数为5个，其中是好瓜的有3个
• 乌黑的个数为4个，其中是好瓜的有4个
• 浅白的个数为2个，其中是好瓜的有0个
  据此，由基尼指数公式，我们可以计算D中的Gini（D，色泽）：
  $$(1-(\frac{3}{5}{)}^2-(\frac{2}{5}{)}^2)\ast \frac{5}{11}+(1-(\frac{3}{4}{)}^2-(\frac{1}{4}{)}^2)\ast \frac{4}{11}=0.35454545...$$
  将训练集的各项属性的基尼指数计算得出后：
  
  最终数值最小的“脐部”作为最优划分属性。

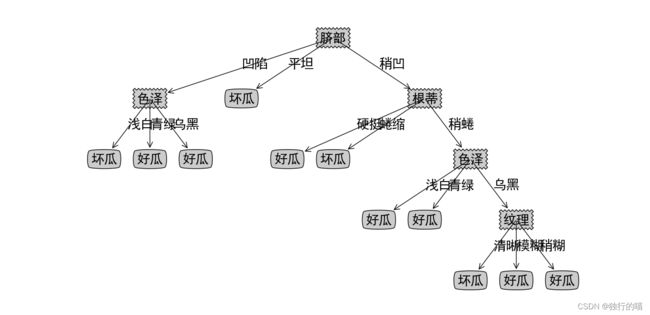
根据“脐部”属性特征的不同，按照脐部为：凹陷，稍凹，平坦，将数据集分为三个子集，也就是构建出决策树的三个子节点。再以每一个子节点为数据集，在排除脐部以外的属性集中，选择出下一个最优划分属性来进行进一步的划分或由递归返回条件变为叶子节点并得出分类标记。依次类推，最终将在递归的划分中创建出整颗决策树。其中将数据集分类再处理再分类的过程体现了分而治之的思想。

三.剪枝处理

剪枝（pruning）是决策树算法对付”过拟合“的主要手段

1.预剪枝

预剪枝是指在决策树生成过程中，对每个结点在划分前先进行估计，若当前结点的划分不能带来决策树泛化性能的提升，则停止划分并将当前结点标记为叶节点，其类型标记为当前结点数据集中总数最多的类别。
预剪枝可以时决策树很多分支不进行展开，降低了过拟合的风险，同时还显著减少了决策树的训练时间开销和测试时间开销。但另一方面，有些分支的当前划分虽然不能提升泛化性能，甚至可能导致泛化性能下降，但在其基础上进行的后续划分却有可能导致泛化性能显著提升。预剪枝基于贪心本质禁止这些分支展开，给预剪枝决策树带来了欠拟合的风险。

2.后剪枝

后剪枝是先从训练集生成一棵完整的决策树，然后自底向上地对非叶节点进行考察，若将该节点对应的子树替换成叶节点能带来决策树泛化性能的提升，则将该子树替换为叶节点。
后剪枝决策树通常比预剪枝决策树保留了更多的分支。一般情形下，后剪枝决策树的欠拟合风险很小，泛化性能往往优于预剪枝决策树。但是后剪枝过程是在生成完全决策树之后进行的，并且自底向上地对树中的所有非叶节点进行逐一考察，因此其训练时间开销比未剪枝决策树和预剪枝决策树都要大得多，也就算法的时间复杂度往往比较大。

四.算法代码

算法代码参考了博文：https://blog.csdn.net/m0_37822685/article/details/100055766

import numpy as np
import matplotlib.pyplot as plt
from pylab import *
import operator

# 特征字典，后面用到了好多次，干脆当全局变量了
featureDic = {
    '色泽': ['浅白', '青绿', '乌黑'],
    '根蒂': ['硬挺', '蜷缩', '稍蜷'],
    '敲声': ['沉闷', '浊响', '清脆'],
    '纹理': ['清晰', '模糊', '稍糊'],
    '脐部': ['凹陷', '平坦', '稍凹'],
    '触感': ['硬滑', '软粘']}

# ***********************画图***********************
# **********************start***********************
# 详情参见机器学习实战决策树那一章

# 定义文本框和箭头格式
decisionNode = dict(boxstyle="sawtooth", fc="0.8")
leafNode = dict(boxstyle="round4", fc="0.8")
arrow_args = dict(arrowstyle="<-")
mpl.rcParams['font.sans-serif'] = ['SimHei']  # 没有这句话汉字都是口口
# mpl.rcParams['axes.unicode_minus'] = False  # 解决保存图像是负号'-'显示为方块的问题


def plotMidText(cntrPt, parentPt, txtString):
    xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0]
    yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1]
    createPlot.ax1.text(xMid, yMid, txtString, fontsize=20)


def plotNode(nodeTxt, centerPt, parentPt, nodeType):  # 绘制带箭头的注解
    createPlot.ax1.annotate(nodeTxt,
                            xy=parentPt,
                            xycoords="axes fraction",
                            xytext=centerPt,
                            textcoords="axes fraction",
                            va="center",
                            ha="center",
                            bbox=nodeType,
                            arrowprops=arrow_args,
                            fontsize=20)


def getNumLeafs(myTree):  # 获取叶节点的数目
    numLeafs = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':
            numLeafs += getNumLeafs(secondDict[key])
        else:
            numLeafs += 1
    return numLeafs


def getTreeDepth(myTree):  # 获取树的层数
    maxDepth = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':
            thisDepth = 1 + getTreeDepth(secondDict[key])
        else:
            thisDepth = 1
        if thisDepth > maxDepth: maxDepth = thisDepth
    return maxDepth


def plotTree(myTree, parentPt, nodeTxt):
    numLeafs = getNumLeafs(myTree)
    getTreeDepth(myTree)
    firstStr = list(myTree.keys())[0]
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW,
              plotTree.yOff)
    plotMidText(cntrPt, parentPt, nodeTxt)
    plotNode(firstStr, cntrPt, parentPt, decisionNode)
    secondDict = myTree[firstStr]
    plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':
            plotTree(secondDict[key], cntrPt, str(key))
        else:
            plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW
            plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff),
                     cntrPt, leafNode)
            plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
    plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD


def createPlot(inTree):
    fig = plt.figure(1, figsize=(600, 30), facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)
    plotTree.totalW = float(getNumLeafs(inTree))
    plotTree.totalD = float(getTreeDepth(inTree))
    plotTree.xOff = -0.5 / plotTree.totalW
    plotTree.yOff = 1.0
    plotTree(inTree, (0.5, 1.0), '')
    plt.show()
# ***********************画图***********************
# ***********************end************************


def getDataSet():
    """
    get watermelon data set 3.0 alpha.
    :return: 训练集合剪枝集以及特征列表。
    """
    # 也可以直接从
    dataSet = [
        ['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],
        ['乌黑', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '好瓜'],
        ['乌黑', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],
        ['青绿', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '好瓜'],
        ['浅白', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],
        ['青绿', '稍蜷', '浊响', '清晰', '稍凹', '软粘', '好瓜'],
        ['乌黑', '稍蜷', '浊响', '稍糊', '稍凹', '软粘', '好瓜'],
        ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '硬滑', '好瓜'],
        ['乌黑', '稍蜷', '沉闷', '稍糊', '稍凹', '硬滑', '坏瓜'],
        ['青绿', '硬挺', '清脆', '清晰', '平坦', '软粘', '坏瓜'],
        ['浅白', '硬挺', '清脆', '模糊', '平坦', '硬滑', '坏瓜'],
        ['浅白', '蜷缩', '浊响', '模糊', '平坦', '软粘', '坏瓜'],
        ['青绿', '稍蜷', '浊响', '稍糊', '凹陷', '硬滑', '坏瓜'],
        ['浅白', '稍蜷', '沉闷', '稍糊', '凹陷', '硬滑', '坏瓜'],
        ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '软粘', '坏瓜'],
        ['浅白', '蜷缩', '浊响', '模糊', '平坦', '硬滑', '坏瓜'],
        ['青绿', '蜷缩', '沉闷', '稍糊', '稍凹', '硬滑', '坏瓜']
    ]

    features = ['色泽', '根蒂', '敲声', '纹理', '脐部', '触感']

    # #得到特征值字典，本来用这个生成的特征字典，还是直接当全局变量方便
    # featureDic = {}
    # for i in range(len(features)):
    #     featureList = [example[i] for example in dataSet]
    #     uniqueFeature = list(set(featureList))
    #     featureDic[features[i]] = uniqueFeature

    # 每种特征的属性个数
    numList = []  # [3, 3, 3, 3, 3, 2]
    for i in range(len(features)):
        numList.append(len(featureDic[features[i]]))
    # # 编码，把文字替换成数字。用1、2、3表示同种特征的不同类型
    # newDataSet = []
    # for dataVec in dataSet:  # 第一每一个数据
    #     dataNum = dataVec[-1]  # 保存数据中类别部分
    #     newData = []
    #     for i in range(len(dataVec) - 1):  # 值为字符的每一列
    #         for j in range(numList[i]):  # 对应列的特征的每一类
    #             if dataVec[i] == featureDic[features[i]][j]:
    #                 newData.append(j + 1)
    #     newData.append(dataNum)  # 编码好的部分和原来的数值部分合并
    #     newDataSet.append(newData)

    newDataSet = np.array(dataSet)
    # 得到训练数据集
    trainIndex = [0, 1, 2, 3, 5, 6, 9, 13, 14, 15, 16]
    trainDataSet = newDataSet[trainIndex]
    # 得到剪枝数据集
    pruneIndex = [4, 7, 8, 10, 11, 12]
    pruneDataSet = newDataSet[pruneIndex]

    return np.array(dataSet), trainDataSet, pruneDataSet, features

# 计算基尼指数
def calGini(dataArr):
    """
    calculate information entropy.
    :param dataArr:
    :param classArr:
    :return: Gini
    """
    numEntries = dataArr.shape[0] #shape [0] 表示行数,即数据集样本总数
    classArr = dataArr[:, -1] #表示是好瓜还是坏瓜
    uniqueClass = list(set(classArr))
    Gini = 1.0
    for c in uniqueClass:
        Gini -= (len(dataArr[dataArr[:, -1] == c]) / float(numEntries)) ** 2
    return Gini


def splitDataSet(dataSet, ax, value):
    """
    按照给点的属性ax和其中一种取值value来划分数据。
    当属性类型为标称数据时，返回一个属性值都为value的数据集。
    input:
        dataSet: 输入数据集，形状为(m,n)表示m个数据，前n-1列个属性，最后一列为类型。
        ax：属性类型
        value: 标称型时为1、2、3等。数值型为形如0.123的数。
    return：
        标称型dataSet返回第ax个属性中值为value组成的集合
    """
    return np.delete(dataSet[dataSet[:, ax] == value], ax, axis=1)


def calSplitGin(dataSet, ax, labels):
    """
    计算给定数据dataSet在属性ax上的基尼指数。
    input：
        dataSet：输入数据集，形状为(m,n)表示m个数据，前n-1列个属性，最后一列为类型。
        labelList：属性列表，如['色泽', '根蒂', '敲声', '纹理', '脐部', '触感']
        ax: 选择用来计算信息增益的属性。0表示第一个属性，1表示第二个属性等。
    return：
        Gini:基尼指数
    """
    newGini = 0.0  # 划分完数据后的基尼指数
    # 对每一种属性
    for j in featureDic[ax]:
        axIndex = labels.index(ax)
        subDataSet = splitDataSet(dataSet, axIndex, j)
        prob = len(subDataSet) / float(len(dataSet))
        if prob != 0:  # prob为0意味着dataSet的ax属性中，没有第j+1种值
            newGini += prob * calGini(subDataSet)
    return newGini


def chooseBestSplit(dataSet, labelList):
    """
    得到基尼指数最小的属性作为最有划分属性。
    input:
        dataSet
        labelList
    return:
        bestFeature: 使得到最大增益划分的属性。
    """
    bestGain = 1
    bestFeature = -1
    n = dataSet.shape[1]
    # 对每一个特征
    for i in range(n - 1):
        newGini = calSplitGin(dataSet, labelList[i], labelList)
        print(f"{labelList[i]}   {newGini}")
        if newGini < bestGain:
            bestFeature = i
            bestGain = newGini

    return bestFeature


def majorityCnt(classList):
    classCount = {}
    for vote in classList:
        if vote not in classCount:
            classCount[vote] = 0
        classCount[vote] += 1
    # classCount.items()将字典的key-value对变成元组对，如{'a':1, 'b':2} -> [('a',1),('b',2)]
    # operator.itemgetter(1)按照第二个元素次序进行排序
    # reverse=True表示从大大到小。[('b',2), ('a',1)]
    sortedClassCount = sorted(classCount.items(),
                              key=operator.itemgetter(1),
                              reverse=True)
    return sortedClassCount[0][0]   # 返回第0个元组的第0个值


def createTree(dataSet, labels):
    """
    通过信息增益递归创造一颗决策树。
    input:
        labels
        dataSet
    return:
        myTree: 返回一个存有树的字典
    """
    classList = dataSet[:, -1]
    # 如果基尼指数为0，即D中样本全属于同一类别，返回
    if calGini(dataSet) == 0:
        return dataSet[0][-1]
    # 属性值为空，只剩下类标签
    if len(dataSet[0]) == 1:
        return majorityCnt(classList)

    # 得到增益最大划分的属性、值
    bestFeatIndex = chooseBestSplit(dataSet, labels)  # bestFeat 是最优划分属性的坐标
    bestFeatLabel = labels[bestFeatIndex] #获得最优属性
    print(f"最优属性为：{bestFeatLabel}")
    myTree = {bestFeatLabel: {}}  # 创建字典，即树的节点。
    # 生成子树的时候要将已遍历的属性删去。数值型不要删除。
    labelsCopy = labels[:]
    del (labelsCopy[bestFeatIndex])
    uniqueVals = featureDic[bestFeatLabel]  # 最好的特征的类别列表
    for value in uniqueVals:  # 标称型的属性值有几种，就要几个子树。
        # Python中列表作为参数类型时，是按照引用传递的，要保证同一节点的子节点能有相同的参数。
        subLabels = labelsCopy[:]    # subLabels = 注意要用[:]，不然还是引用
        subDataSet = splitDataSet(dataSet, bestFeatIndex, value)
        print(subDataSet)
        print("----------")
        if len(subDataSet) != 0:
            myTree[bestFeatLabel][value] = createTree(subDataSet, subLabels)
        else:
            # 计算D中样本最多的类
            myTree[bestFeatLabel][value] = majorityCnt(classList)

    return myTree


def classify(data, featLabels, Tree):
    """
    通过决策树对一条数据分类
    :param featLabels:
    :param data:
    :param Tree:
    :return: 分类
    """
    firstStr = list(Tree.keys())[0]  # 父节点
    secondDict = Tree[firstStr]  # 父节点下的子树，即子字典
    featIndex = featLabels.index(firstStr)  # 当前属性标识的位置
    classLabel = ""
    for key in secondDict.keys():  # 遍历该属性下的不同类
        if data[featIndex] == key:  # 如果数据中找到了匹配的属性类别
            # 如果不是叶子节点，继续向下遍历
            if type(secondDict[key]).__name__ == 'dict':
                classLabel = classify(data, featLabels, secondDict[key])
            # 如果是叶子节点，返回该叶子节点的类型
            else:
                classLabel = secondDict[key]
    return classLabel


def calAccuracy(dataSet, labels, Tree):
    """
    计算已有决策树的精度
    :param dataSet:
    :param labels: ['色泽', '根蒂', '敲声', '纹理', '脐部', '触感']
    :param Tree:
    :return: 决策树精度
    """
    cntCorrect = 0
    size = len(dataSet)
    for i in range(size):
        pre = classify(dataSet[i], labels, Tree)
        if pre == dataSet[i][-1]:
            cntCorrect += 1
    return cntCorrect / float(size)


def cntAccNums(dataSet, pruneSet):
    """
    用于剪枝，用dataSet中多数的类作为节点类，计算pruneSet中有多少类是被分类正确的，然后返回正确
    分类的数目。
    :param dataSet: 训练集
    :param pruneSet: 测试集
    :return: 正确分类的数目
    """
    nodeClass = majorityCnt(dataSet[:, -1])
    rightCnt = 0
    for vect in pruneSet:
        if vect[-1] == nodeClass:
            rightCnt += 1
    return rightCnt


def prePruning(dataSet, pruneSet, labels):
    """
    每到一个节点要划分的时候：
    1. 用这个节点上数据投票得出这个节点的类，即是"好瓜"还是"坏瓜"。
    2. 用这个投票出来的类计算测试集中正确的点数。
    3. 尝试计算一个节点向下划分时测试点的正确数。假如，当前属性为"脐部"，有三种"凹陷",
    "稍凹","平坦"，则可将训练集和测试集按照这三种属性值分为三部分，分别计算分类正确的点数并求和。
    4 若尝试划分得到的正确点数少于不划分时得到的正确点数，则返回不划分时节点的类，否则继续划分。
    :param dataSet: 训练数据集
    :param pruneSet: 预剪枝数据集
    :param labels:  属性标签
    :return:
    """
    classList = dataSet[:, -1]

    if calGini(dataSet) == 0:
        return dataSet[0][-1]

    if len(dataSet[0]) == 1:
        return majorityCnt(classList)

    # 获取最好特征
    bestFeat = chooseBestSplit(dataSet, labels)
    bestFeatLabel = labels[bestFeat]
    # 计算初始正确率
    baseRightNums = cntAccNums(dataSet, pruneSet)
    # 得到最好划分属性取值
    features = featureDic[bestFeatLabel]
    # 计算尝试划分节点时的正确率
    splitRightNums = 0.0
    for value in features:
        # 每个属性取值得到的子集
        subDataSet = splitDataSet(dataSet, bestFeat, value)
        if len(subDataSet) != 0:
            # 把用来剪枝的子集也按照相应属性值划分下去
            subPruneSet = splitDataSet(pruneSet, bestFeat, value)
            splitRightNums += cntAccNums(subDataSet, subPruneSet)
    if baseRightNums < splitRightNums:  # 如果不划分的正确点数少于尝试划分的点数，则继续划分。
        myTree = {bestFeatLabel: {}}
    else:
        return majorityCnt(dataSet[:, -1])  # 否则，返回不划分时投票得到的类

    # 以下代码和不预剪枝的代码大致相同，一点不同在于每次测试集也要参与划分。
    for value in features:
        subLabels = labels[:]
        subDataSet = splitDataSet(dataSet, bestFeat, value)
        subPruneSet = splitDataSet(pruneSet, bestFeat, value)
        if len(subDataSet) != 0:
            myTree[bestFeatLabel][value] = prePruning(subDataSet, subPruneSet, subLabels)
        else:
            # 计算D中样本最多的类
            myTree[bestFeatLabel][value] = majorityCnt(classList)
    return myTree


def postPruning(dataSet, pruneSet, labels):
    """
    后剪枝的思想就是，在决策树每一条分支到达叶子节点时，分别计算剪枝和不剪枝时，位于该节点上的
    测试数据，被正确判定的数量孰大孰小，以此为依据来决定是否剪枝。
    :param dataSet:
    :param pruneSet:
    :param labels:
    :return:
    """
    classList = dataSet[:, -1]
    # 如果基尼指数为0，即D中样本全属于同一类别，返回
    if calGini(dataSet) == 0:
        return dataSet[0][-1]
    # 属性值为空，只剩下类标签
    if len(dataSet[0]) == 1:
        return majorityCnt(classList)

    # 得到增益最大划分的属性、值
    bestFeat = chooseBestSplit(dataSet, labels)
    bestFeatLabel = labels[bestFeat]
    myTree = {bestFeatLabel: {}}  # 创建字典，即树的节点。
    # 生成子树的时候要将已遍历的属性删去。数值型不要删除。
    labelsCopy = labels[:]
    del (labelsCopy[bestFeat])
    uniqueVals = featureDic[bestFeatLabel]  # 最好的特征的类别列表
    for value in uniqueVals:  # 标称型的属性值有几种，就要几个子树。
        # Python中列表作为参数类型时，
        #
        # 是按照引用传递的，要保证同一节点的子节点能有相同的参数。
        subLabels = labelsCopy[:]  # subLabels = 注意要用[:]，不然还是引用
        subPrune = splitDataSet(pruneSet, bestFeat, value)
        subDataSet = splitDataSet(dataSet, bestFeat, value)
        if len(subDataSet) != 0:
            myTree[bestFeatLabel][value] = postPruning(subDataSet, subPrune, subLabels)
        else:
            # 计算D中样本最多的类
            myTree[bestFeatLabel][value] = majorityCnt(classList)

    # 后剪枝，如果到达叶子节点，尝试剪枝。
    # 计算未剪枝时，测试集的正确数
    numNoPrune = 0.0
    for value in uniqueVals:
        subDataSet = splitDataSet(dataSet, bestFeat, value)
        if len(subDataSet) != 0:
            subPrune = splitDataSet(pruneSet, bestFeat, value)
            numNoPrune += cntAccNums(subDataSet, subPrune)
    # 计算剪枝后，测试集正确数
    numPrune = cntAccNums(dataSet, pruneSet)
    # 比较决定是否剪枝, 如果剪枝后该节点上测试集的正确数变多了，则剪枝。
    if numNoPrune < numPrune:
        return majorityCnt(dataSet[:, -1])  # 直接返回节点上训练数据的多数类为节点类。

    return myTree


def main():
    dataSet, trainData, pruneData, labelList = getDataSet()
    # 用训练集训练一颗树并画图
    myTree = createTree(trainData, labelList)
    print(myTree)
    createPlot(myTree)
    # 画预剪枝树
    preTree = prePruning(trainData, pruneData, labelList)
    # createPlot(preTree)
    # 画后剪枝树
    postPTree = postPruning(trainData, pruneData, labelList)
    print(postPTree)
    # createPlot(postPTree)
    # 计算未剪枝的精度
    print(f"full tree's train accuracy = {calAccuracy(trainData, labelList, myTree)},"
          f"test accuracy = {calAccuracy(pruneData, labelList, myTree)}\n")
    # 计算预剪枝精度
    print(f"pre pruning tree's train accuracy = {calAccuracy(trainData, labelList, myTree)},"
          f"test accuracy = {calAccuracy(pruneData, labelList, preTree)}\n")
    # 计算后剪枝精度
    print(f"post pruning tree's train accuracy = {calAccuracy(trainData, labelList, myTree)},"
          f"test accuracy = {calAccuracy(pruneData, labelList, postPTree)}\n")

if __name__ == '__main__':
    main()