西瓜决策树-sklearn实现
西瓜决策树-sklearn实现
- 读取数据
- 数据编码
- ID3算法
- CART算法
-
- 基尼指数
- 参考资料
读取数据
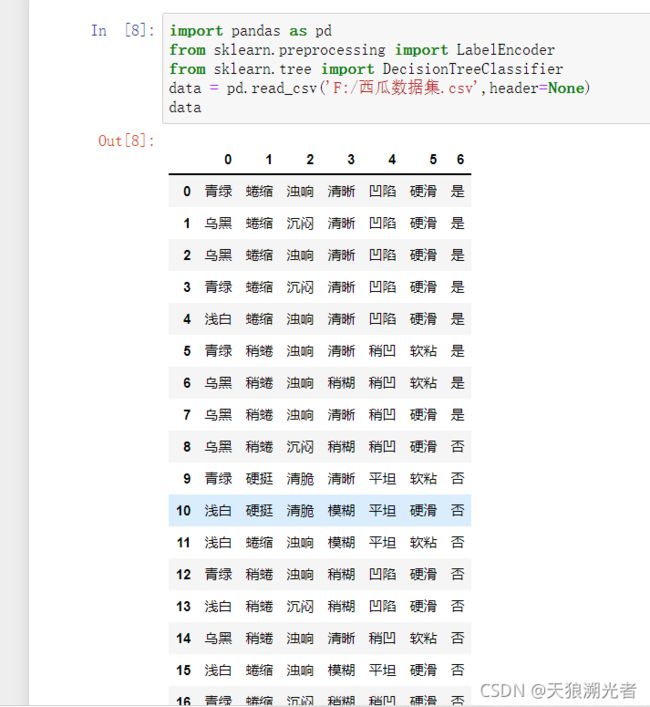
import pandas as pd
from sklearn.preprocessing import LabelEncoder
from sklearn.tree import DecisionTreeClassifier
data = pd.read_csv('F:/西瓜数据集.csv',header=None)
data
数据编码
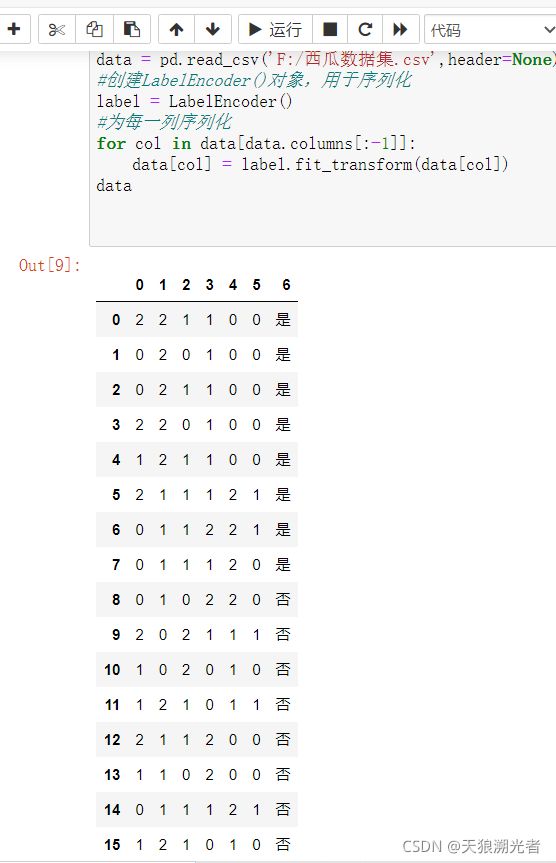
#创建LabelEncoder()对象,用于序列化
label = LabelEncoder()
#为每一列序列化
for col in data[data.columns[:-1]]:
data[col] = label.fit_transform(data[col])
data
ID3算法
熵和信息增益
设S是训练样本集,它包括n个类别的样本,这些方法用Ci表示,那么熵和信息增益用下面公式表示:
信息熵:
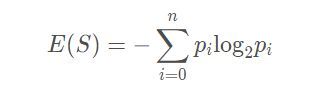
其中pi表示Ci的概率
样本熵:
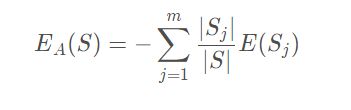
其中Si表示根据属性A划分的S的第i个子集,S和Si表示样本数目
信息增益:
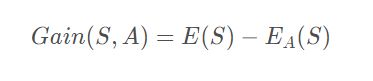
ID3中样本分布越均匀,它的信息熵就越大,所以其原则就是样本熵越小越好,也就是信息增益越大越好。
# 采用ID3拟合
dtc = DecisionTreeClassifier(criterion='entropy')
# 进行拟合
dtc.fit(data.iloc[:,:-1].values.tolist(),data.iloc[:,-1].values)
# 标签对应编码
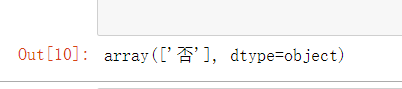
result = dtc.predict([[0,0,0,0,0,0]])
#拟合结果
result
CART算法
CART算法构造的是二叉决策树,决策树构造出来后同样需要剪枝,才能更好的应用于未知数据的分类。CART算法在构造决策树时通过基尼系数来进行特征选择。
基尼指数
基尼指数:若某样本数据分为类,数据属于第k类的概率为,则样本数据的基尼指数定义为:

对于训练样本集,其基尼指数如下:
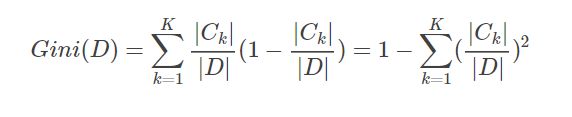
如果样本集合D根据特征Am的取值可以分为两部分D1和D2,那么在特征Am的条件下,D的基尼指数如下:
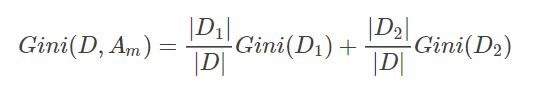
基尼指数Gini(D)表征着数据集D的不确定性,而在特征Am的条件下,D的基尼指数则表征着在特征Am确定的条件下D的不确定性,因此基尼指数之差和信息增益及信息增益比一样,可以表征特征Am对数据集D的分类的能力。
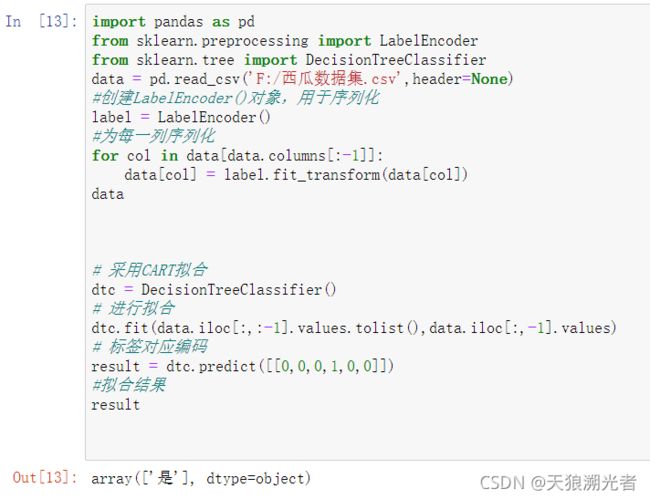
# 采用CART拟合
dtc = DecisionTreeClassifier()
# 进行拟合
dtc.fit(data.iloc[:,:-1].values.tolist(),data.iloc[:,-1].values)
# 标签对应编码
result = dtc.predict([[0,0,0,1,0,0]])
#拟合结果
result
参考资料
-
[1] 决策树ID3,C4.5,CART算法及实现
-
[2] 西瓜决策树-sklearn实现