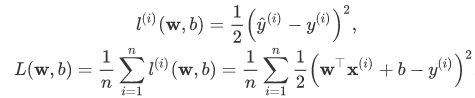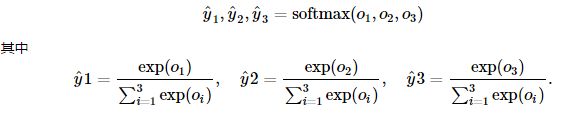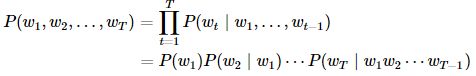线性回归、多层感知机、文本预处理、循环神经网络学习笔记（打卡1）

一、线性回归

1.线性回归的数学假设：假设输入的x和y是线性关系，输入的x和y满足，其中e为误差，满足均值为0，方差为某一确定值的正太分布

2.线性回归的建模：

3.损失函数：简单的损失函数可以选择为平方损失

二、Softmax 

对于神经网络中，直接使用输出层的输出有两个问题：

1. 一方面，由于输出层的输出值的范围不确定，我们难以直观上判断这些值的意义。例如，刚才举的例子中的输出值10表示“很置信”图像类别为猫，因为该输出值是其他两类的输出值的100倍。但如果o1=o3=103o1=o3=103，那么输出值10却又表示图像类别为猫的概率很低。
2. 另一方面，由于真实标签是离散值，这些离散值与不确定范围的输出值之间的误差难以衡量。

因此，softmax将输出值归一化为0到1的概率值：

三、交叉熵

训练目标可以设为预测概率分布尽可能接近真实的. 由于我们其实并不需要预测概率完全等于标签概率，而平方损失则过于严格为了改进这个问题是使用更适合衡量两个概率分布差异的测量函数。其中，交叉熵（cross entropy）是一个常用的衡量方法：

交叉熵只关心对正确类别的预测概率，因为只要其值足够大，就可以确保分类结果正确。当然，遇到一个样本有多个标签时，例如图像里含有不止一个物体时，我们并不能做这一步简化。但即便对于这种情况，交叉熵同样只关心对图像中出现的物体类别的预测概率。

假设训练数据集的样本数为nn，交叉熵损失函数定义为：

其中Θ代表模型参数。

四、多层感知机

多层感知机（MLP，Multilayer Perceptron）也叫人工神经网络（ANN，Artificial Neural Network），除了输入输出层，它中间可以有多个隐层，最简单的MLP只含一个隐层，即三层的结构，如下图：

从上图可以看到，多层感知机层与层之间是全连接的。多层感知机最底层是输入层，中间是隐藏层，最后是输出层。 

隐藏层的神经元：首先它与输入层是全连接的，假设输入层用向量X表示，则隐藏层的输出就是 f (W1X+b1)，W1是权重（也叫连接系数），b1是偏置，函数f 可以是常用的sigmoid函数、tanh函数或者ReLU：

1.Sigmoid函数

函数数学形式：

Sigmoid函数输入一个实值的数，然后将其压缩到0-1的范围内。特别地，大的负数被映射成0，大的正数被映射成1。sigmoid 函数曾经被使用的很多，因为它能够很好的表达“激活”的意思，未激活就是0，激活则是1。而现在sigmoid已经不怎么常用了，主要是因为它有两个缺点：

（1）容易饱和。当输入非常大或者非常小的时候，神经元的梯度就接近于0了（也就是“饱和”的概念）。这就使得我们在反向传播算法中反向传播接近于0的梯度，导致最终权重基本没什么更新，我们就无法递归地完成训练了。另外，还需要注意参数的初始值来尽量避免饱和的情况。如果你的初始值很大的话，大部分神经元可能都会处在饱和的状态，它们的梯度都很接近于0，这会导致网络变的很难学习。

（2）Sigmoid函数的输出不是0均值的。这是我们不希望的，因为这会导致后层的神经元的输入是非0均值的信号，从而对梯度产生影响。（假设后层神经元的输入都为正(e.g. x>0 in f=wTx+b),那么对w求局部梯度则都为正，这样在反向传播的过程中w就会都往正方向更新，导致有一种捆绑的效果，使得收敛缓慢。

 

2.tanh函数（双曲正切函数）

实际上，tanh 是sigmoid的变形：

与sigmoid不同的是，tanh 是0均值的。因此，实际应用中，tanh 会比sigmoid效果更好。

 

3.ReLU函数（线性纠正函数）

函数表达式：

输入信号小于0时，输出为0；大于0时，输出等于输入。

优点：1）收敛速度快。相比于tanh函数，收敛速度可以加快6倍左右。

        （原因：ReLU函数不会饱和。对于大于0的部分其导数值恒为1。应用反向传播算法时能够将梯度很好地传到较前面的网络）

      2）在x>0的区域不会出现“饱和”问题。

3）计算效率高。相比于 sigmoid/tanh需要计算指数，ReLU只需要一个阈值就可以得到激活值，计算复杂度较低。

缺点：1）在训练的时候很“脆弱”，一不小心有可能导致神经元“坏死”。举个例子：由于ReLU在x<0时梯度为0，这样就导致负的梯度在ReLU中会被置零，而且这个神经元有可能再也不会被任何数据激活。如果这个情况发生了，那么这个神经元之后的梯度就永远是0了，这也就意味着这个神经元坏死了，不再对任何数据有所响应。

     2）输出不是0均值的。

缺点的解决方法：

对ReLU函数进行一定的改进。如Leaky-ReLU、Parametric ReLU等。

1）Leaky-ReLU函数。和ReLU不同，当x<0时，它的值不再是0，而是一个有较小斜率(如0.01等)的函数。这样，既修正了数据分布，又保留了一些负轴的值，使得负轴信息不会全部丢失；同时使输出更接近0均值。

2）Parametric ReLU函数。原来 Leaky ReLU 中的负半轴函数的斜率，通常是通过先验知识人工赋值的。 而Parametric ReLU函数将该斜率作为一个参数进行训练。

五、文本预处理

文本是一类序列数据，一篇文章可以看作是字符或单词的序列，文本数据的常见预处理步骤，预处理通常包括四个步骤：

1. 读入文本
2. 分词（一个句子划分成若干个词（token），转换为一个词的序列。）
3. 建立字典，将每个词映射到一个唯一的索引（index）（为了方便模型处理，需要将字符串转换为数字。因此通过构建一个字典（vocabulary），可以将每个词映射到一个唯一的索引编号。）
4. 将文本从词的序列转换为索引的序列，方便输入模型

用现有工具进行分词

有一些现有的工具可以很好地进行分词，在这里简单介绍其中的两个：spaCy和NLTK。

下面是一个简单的例子：

text = "Mr. Chen doesn't agree with my suggestion."

spaCy:
import spacy
nlp = spacy.load('en_core_web_sm')
doc = nlp(text)
print([token.text for token in doc])#['Mr.', 'Chen', 'does', "n't", 'agree', 'with', 'my', 'suggestion', '.']

NLTK:

from nltk.tokenize import word_tokenize
from nltk import data
data.path.append('/home/kesci/input/nltk_data3784/nltk_data')
print(word_tokenize(text))#['Mr.', 'Chen', 'does', "n't", 'agree', 'with', 'my', 'suggestion', '.']

六、语言模型

一段自然语言文本可以看作是一个离散时间序列，给定一个长度为TT的词的序列w1,w2,…,wTw1,w2,…,wT，语言模型的目标就是评估该序列是否合理，即计算该序列的概率：

P(w1,w2,…,wT).P(w1,w2,…,wT

语言模型：

假设序列w1,w2,…,wTw1,w2,…,wT中的每个词是依次生成的，我们有：

 例如，一段含有4个词的文本序列的概率

  P(w1,w2,w3,w4)=P(w1)P(w2∣w1)P(w3∣w1,w2)P(w4∣w1,w2,w3).
  P(w1,w2,w3,w4)=P(w1)P(w2∣w1)P(w3∣w1,w2)P(w4∣w1,w2,w3).

  语言模型的参数就是词的概率以及给定前几个词情况下的条件概率。设训练数据集为一个大型文本语料库，如维基百科的所有条目，词的概率可以通过该词在训练数据集中的相对词频来计算，例如， w1w1 的概率可以计算为：

  P^(w1)=n(w1)n
  P^(w1)=n(w1)n

  其中 n(w1)n(w1) 为语料库中以 w1w1 作为第一个词的文本的数量， nn 为语料库中文本的总数量。

  类似的，给定 w1w1 情况下， w2w2 的条件概率可以计算为：

  P^(w2∣w1)=n(w1,w2)n(w1)
  P^(w2∣w1)=n(w1,w2)n(w1)

  其中 n(w1,w2)n(w1,w2) 为语料库中以 w1w1 作为第一个词， w2w2 作为第二个词的文本的数量。

n元语法
  序列长度增加，计算和存储多个词共同出现的概率的复杂度会呈指数级增加。 nn 元语法通过马尔可夫假设简化模型，马尔科夫假设是指一个词的出现只与前面 nn 个词相关，即 nn 阶马尔可夫链（Markov chain of order nn ），如果 n=1n=1 ，那么有 P(w3∣w1,w2)=P(w3∣w2)P(w3∣w1,w2)=P(w3∣w2) 。基于 n−1n−1 阶马尔可夫链，我们可以将语言模型改写为

  P(w1,w2,…,wT)=∏t=1TP(wt∣wt−(n−1),…,wt−1).
  P(w1,w2,…,wT)=∏t=1TP(wt∣wt−(n−1),…,wt−1).

  以上也叫 nn 元语法（ nn -grams），它是基于 n−1n−1 阶马尔可夫链的概率语言模型。例如，当 n=2n=2 时，含有4个词的文本序列的概率就可以改写为：

P(w1,w2,w3,w4)=P(w1)P(w2∣w1)P(w3∣w1,w2)P(w4∣w1,w2,w3)=P(w1)P(w2∣w1)P(w3∣w2)P(w4∣w3)
P(w1,w2,w3,w4)=P(w1)P(w2∣w1)P(w3∣w1,w2)P(w4∣w1,w2,w3)=P(w1)P(w2∣w1)P(w3∣w2)P(w4∣w3)

当 nn 分别为1、2和3时，我们将其分别称作一元语法（unigram）、二元语法（bigram）和三元语法（trigram）。例如，长度为4的序列 w1,w2,w3,w4w1,w2,w3,w4 在一元语法、二元语法和三元语法中的概率分别为

P(w1,w2,w3,w4)P(w1,w2,w3,w4)P(w1,w2,w3,w4)=P(w1)P(w2)P(w3)P(w4),=P(w1)P(w2∣w1)P(w3∣w2)P(w4∣w3),=P(w1)P(w2∣w1)P(w3∣w1,w2)P(w4∣w2,w3).
P(w1,w2,w3,w4)=P(w1)P(w2)P(w3)P(w4),P(w1,w2,w3,w4)=P(w1)P(w2∣w1)P(w3∣w2)P(w4∣w3),P(w1,w2,w3,w4)=P(w1)P(w2∣w1)P(w3∣w1,w2)P(w4∣w2,w3).

当 nn 较小时， nn 元语法往往并不准确。例如，在一元语法中，由三个词组成的句子“你走先”和“你先走”的概率是一样的。然而，当 nn 较大时， nn 元语法需要计算并存储大量的词频和多词相邻频率。
 

七、循环神经网络

循环神经网络（Recurrent Neural Network, RNN）是一类以序列（sequence）数据为输入，在序列的演进方向进行递归（recursion）且所有节点（循环单元）按链式连接的递归神经网络（recursive neural network） 。
  对循环神经网络的研究始于二十世纪80-90年代，并在二十一世纪初发展为深度学习（deep learning）算法之一 ，其中双向循环神经网络（Bidirectional RNN, Bi-RNN）和长短期记忆网络（Long Short-Term Memory networks，LSTM）是常见的的循环神经网络 。
  循环神经网络具有记忆性、参数共享并且图灵完备（Turing completeness），因此在对序列的非线性特征进行学习时具有一定优势 。循环神经网络在自然语言处理（Natural Language Processing, NLP），例如语音识别、语言建模、机器翻译等领域有应用，也被用于各类时间序列预报。引入了卷积神经网络（Convoutional Neural Network,CNN）构筑的循环神经网络可以处理包含序列输入的计算机视觉问题。
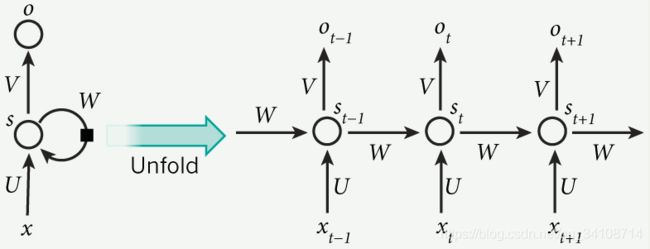
  RNN 的隐藏层的值 s 不仅仅取决于当前这次的输入 x，还取决于上一次隐藏层的值 s：
这个过程画成简图是这个样子：

其中，t 是时刻， x 是输入层， s 是隐藏层， o 是输出层，矩阵 W 就是隐藏层上一次的值作为这一次的输入的权重。