二叉搜索树--进阶篇之平衡二叉搜索树
在二叉查找树的基础上，尽管其查找，插入以及删除操作的平均运行时间为O(logn),但是由于没有对树的形状进行限制，所以最差情况会退化为一个线性结构，最差的运行时间是O(n)。
平衡二叉树（AVL树），它或者是一颗空树，或者是具有如下性质的二叉树：它的左子树和右子树都是平衡二叉树，就可以强行限制树的平衡性，使得左右子树的深度之差绝对值不超过1。定义平衡二叉树的平衡因子Balance Factor 为：改节点的左子树深度减去它的右子树的深度，或者是该子树的右节点的深度减去左子树的深度。对于平衡二叉树，所有节点的平衡因子只可能为-1,0,1。
在上一篇的二叉树的基础上，平衡二叉树的查找和二叉查找树的相同，AVL的插入操作是在二叉查找树的基础上判断当前的场景，按照场景进行平衡操作。AVL的删除操作也一样。区别就在于插入和删除之后要写一个旋转算法去维持平衡，维持平衡需要借助一个节点高度的属性。
一、旋转操作背景
在这之前我们要先了解一下4种导致不平衡的场景：
对于一个平衡的节点，由于任意节点最多有两个儿子，因此高度不平衡时，此节点的两颗子树的高度差2.容易看出，这种不平衡出现在下面四种情况：
1、6节点的左子树3节点高度比右子树7节点大2，左子树3节点的左子树1节点高度大于右子树4节点，这种情况成为左左。
2、6节点的左子树2节点高度比右子树7节点大2，左子树2节点的左子树1节点高度小于右子树4节点，这种情况成为左右。
3、2节点的左子树1节点高度比右子树5节点小2，右子树5节点的左子树3节点高度大于右子树6节点，这种情况成为右左。
4、2节点的左子树1节点高度比右子树4节点小2，右子树4节点的左子树3节点高度小于右子树6节点，这种情况成为右右。
从图2中可以可以看出，1和4两种情况是对称的，这两种情况的旋转算法是一致的，只需要经过一次旋转就可以达到目标，我们称之为单旋转。2和3两种情况也是对称的，这两种情况的旋转算法也是一致的，需要进行两次旋转，我们称之为双旋转。
1.1 单旋转
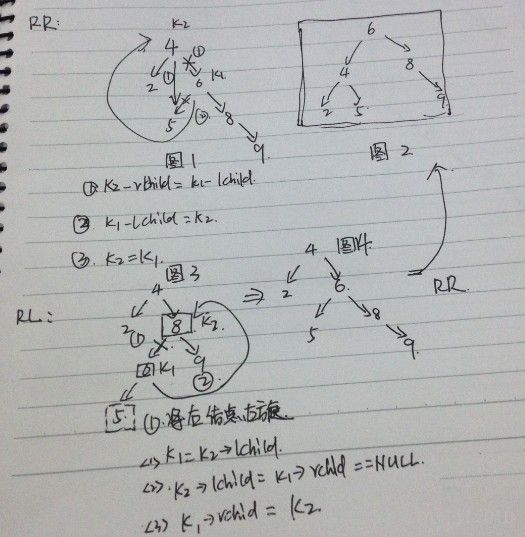
单旋转是针对于左左和右右这两种情况的解决方案，这两种情况是对称的，只要解决了左左这种情况，右右就很好办了。图3是左左情况的解决方案，节点k2不满足平衡特性，因为它的左子树k1比右子树Z深2层，而且k1子树中，更深的一层的是k1的左子树X子树，所以属于左左情况。
为使树恢复平衡，我们把k1变成这棵树的根节点，因为k2大于k1，把k2置于k1的右子树上，而原本在k1右子树的Y大于k1，小于k2，就把Y置于k2的左子树上，这样既满足了二叉查找树的性质，又满足了平衡二叉树的性质。
这样的操作只需要一部分指针改变，结果我们得到另外一颗二叉查找树，它是一棵AVL树，因为X向上一移动了一层，Y还停留在原来的层面上，Z向下移动了一层。整棵树的新高度和之前没有在左子树上插入的高度相同，插入操作使得X高度长高了。因此，由于这颗子树高度没有变化，所以通往根节点的路径就不需要继续旋转了。
代码如下：
//左左情况下的旋转
template
void AVLTree:: SingRotateLeft (TreeNode* &k2)
{
TreeNode* k1;
k1=k2->lson;
k2->lson=k1->rson;
k1->rson=k2;
k2=k1;
k2->hgt=Max(height(k2->lson),height(k2->rson))+1;
k1->hgt=Max(height(k1->lson),k2->hgt)+1;
}
//右右情况下的旋转
template
void AVLTree::SingRotateRight(TreeNode* &k2)
{
TreeNode* k1;
k1=k2->rson;
k2->rson=k1->lson;
k1->lson=k2;
k2 = k1; //由于最后是通过引用传值，需要把k1赋值给k2，带到函数外
k2->hgt=Max(height(k2->lson),height(k2->rson))+1;
k1->hgt=Max(height(k1->rson),k2->hgt)+1;
}
1.2：双旋转
对于左右和右左这两种情况，单旋转不能使它达到一个平衡状态，要经过两次旋转。双旋转是针对于这两种情况的解决方案，同样的，这样两种情况也是对称的，只要解决了左右这种情况，右左就很好办了。图4是左右情况的解决方案，节点k3不满足平衡特性，因为它的左子树k1比右子树Z深2层，而且k1子树中，更深的一层的是k1的右子树k2子树，所以属于左右情况。
为使树恢复平衡，我们需要进行两步，第一步，把k1作为根，进行一次右右旋转，旋转之后就变成了左左情况，所以第二步再进行一次左左旋转，最后得到了一棵以k2为根的平衡二叉树树。
代码如下：
// 左右情况的旋转
template< class T>
void AVLTree::DoubleRotateLR(TreeNode* &k3)
{
SingRotateRight(k3->lson);//将左儿子进行右旋转
SingRotateLeft(k3);//将根节点进行左旋转
}
// 右左情况的旋转
template< class T>
void AVLTree::DoubleRotateRL(TreeNode* &k3)
{
SingRotateLeft(k3->rson);
SingRotateRight(k3);
}
template< class T>
void AVLTree
{
SingRotateRight(k3->lson);//将左儿子进行右旋转
SingRotateLeft(k3);//将根节点进行左旋转
}
// 右左情况的旋转
template< class T>
void AVLTree
{
SingRotateLeft(k3->rson);
SingRotateRight(k3);
}
举个例子说明下：图一插入9，图3插入5,最后图一经过RR旋转变为图2， 图3先经过左左旋转，变为图一，后面的步骤相同：
二、AVL的插入操作
插入的方法和二叉查找树基本一样，区别是，插入完成后需要从插入的节点开始维护一个到根节点的路径，每经过一个节点都要维持树的平衡。维持树的平衡要根据高度差的特点选择不同的旋转算法。
代码如下：
（注：修改了参考代码的错误。如前三种情景没有加node->hgt++;最后一行的根节点的高度没有加1，还有需要返回值，来判断是否应该高度加1，因为出现插入重复数据时，其插入结果是失败的）
//插入
template
int AVLTree::insertpri(TreeNode* &node,T x)
{
int tmp1 =0,tmp2=0;
bool brotate = false;
if(node==NULL)//如果当前节点为空，加入该节点
{
node=new TreeNode();
node->data=x;
node->hgt++;
cout<<"nodea"<data<<"height"<hgt<data>x)//如果x小于节点的值,就继续在节点的左子树中插入x
{
tmp1=insertpri(node->lson,x);
if(tmp1 == 1)
{
node->hgt++;
cout<<"nodeb"<data<<"height"<hgt<lson)-height(node->rson))
{
brotate = true;
if(xlson->data)
{
cout<<"ll"<datarson,x);
if(tmp2 == 1)
{
node->hgt++;
cout<<"nodec"<data<<"height"<hgt<rson)-height(node->lson))
{
if(x>node->rson->data)
{
cout<<"rr"<freq);//如果相等,就把频率加1，但是有个问题沿途遇到的节点加1了，但是其他的就没有，所以会导致有重复数据时候错误和乱套
cout<<"nodee"<data<<"freq"<freq<hgt=Max(height(node->lson),height(node->rson))+1;//更新存在左右子树的根节点的高度
if(tmp1 || tmp2)
{
return 1;
}
return 0;
} 三、AVL的删除操作
删除操作同二叉搜索树相同，不同的是需要在删除后判断是否平衡，然后进行平衡操作。这个问题现在结论出来了，但是其中的代码没有一步一步的验证
注：删除操作也在参考的代码中修改了很多的问题。
//删除
template
int AVLTree::Deletepri(TreeNode* &node,T x)
{
int tmp1=0,tmp2 = 0;
if(node==NULL)
{
return 0 ;//没有找到值是x的节点
}
if(x < node->data)
{
//如果x小于节点的值,就继续在节点的左子树中删除x
tmp1 = Deletepri(node->lson,x);
if(tmp1==1)
{
node->hgt--;
//找到节点node，返回上一层
if(2==height(node->lson)-height(node->rson))//平衡因子定义为右儿子高度减去左儿子的高度
{
//注意 需要考虑节点node->lson->rson==NULL的情况，这个时候求height是会挂掉的
if((node->lson->rson!=NULL&&(height(node->lson->rson)>height(node->lson->lson))) || (node->lson->rson==NULL&&height(node->lson->rson)>0) )
{
cout<<"lr"< node->data)
{
tmp2 = Deletepri(node->rson,x);//如果x大于节点的值,就继续在节点的右子树中删除x
if(tmp2==1)
{
node->hgt--;
if(2==height(node->rson)-height(node->lson))
{
if((node->rson->lson!=NULL&&(height(node->rson->lson)>height(node->rson->rson))) || (node->rson->lson==NULL&&height(node->rson->lson)>0) )
{
cout<<"rl"<lson&&node->rson)//此节点有两个儿子
{
TreeNode* temp=node->rson;//temp指向节点的右儿子
while(temp->lson!=NULL) temp=temp->lson;//找到右子树中值最小的节点
//把右子树中最小节点的值赋值给本节点
node->data=temp->data;
node->freq=temp->freq;
Deletepri(node->rson,temp->data);//删除右子树中最小值的节点
if(2==height(node->lson)-height(node->rson))
{
if(node->lson->rson!=NULL&& (height(node->lson->rson)>height(node->lson->lson) ))
{
cout<<"equal lr"<* temp=node;
TreeNode* nonenullnode=NULL;
if(node->lson==NULL)//有右儿子或者没有儿子
{
node=node->rson;
}
else if(node->rson==NULL)//有左儿子
{
node=node->lson;
}
delete(temp);
temp=NULL;
}
return 1;
}
//if(node==NULL) return 0;
node->hgt=Max(height(node->lson),height(node->rson))+1;
if(tmp1 || tmp2)
{
return 1;
}
else return 0;
} 四、附上全部代码和验证
#include
using namespace std;
//AVL树节点信息
template
class TreeNode
{
public:
TreeNode():lson(NULL),rson(NULL),freq(1),hgt(-1){}
T data;//值
int hgt;//以此节点为根的树的高度
unsigned int freq;//频率
TreeNode* lson;//指向左儿子的地址
TreeNode* rson;//指向右儿子的地址
};
//template
//typedef TreeNode* Tree;
//AV类的属性和方法声明
template
class AVLTree
{
private:
TreeNode* root;//根节点
int insertpri(TreeNode* &node, T x);//插入
TreeNode* findpri(TreeNode* node, T x);//查找
void insubtree(TreeNode* node);//中序遍历
int Deletepri(TreeNode* &node, T x);//删除
int height(TreeNode* node);//求树的高度
void SingRotateLeft(TreeNode* &k2);//左左情况下的旋转
void SingRotateRight(TreeNode* &k2);//右右情况下的旋转
void DoubleRotateLR(TreeNode* &k3);//左右情况下的旋转
void DoubleRotateRL(TreeNode* &k3);//右左情况下的旋转
int Max(int cmpa,int cmpb);//求最大值
void InorderBST(TreeNode* node) ;
public:
AVLTree():root(NULL){}
void insert(T x);//插入接口
TreeNode* find(T x);//查找接口
void Delete(T x);//删除接口
void traversal();//遍历接口
void print();
};
//计算以节点为根的树的高度
template
int AVLTree::height(TreeNode* node)
{
if(node!=NULL)
return node->hgt;
return -1;
}
//求最大值
template
int AVLTree::Max(int cmpa,int cmpb)
{
return cmpa>cmpb?cmpa:cmpb;
}
//左左情况下的旋转
template
void AVLTree:: SingRotateLeft (TreeNode* &k2)
{
TreeNode* k1;
k1=k2->lson;
k2->lson=k1->rson;
k1->rson=k2;
k2=k1;
k2->hgt=Max(height(k2->lson),height(k2->rson))+1;
k1->hgt=Max(height(k1->lson),k2->hgt)+1;
}
//右右情况下的旋转
template
void AVLTree::SingRotateRight(TreeNode* &k2)
{
TreeNode* k1;
k1=k2->rson;
k2->rson=k1->lson;
k1->lson=k2;
k2 = k1; //由于最后是通过引用传值，需要把k1赋值给k2，带到函数外
k2->hgt=Max(height(k2->lson),height(k2->rson))+1;
k1->hgt=Max(height(k1->rson),k2->hgt)+1;
}
//左右情况的旋转
template
void AVLTree::DoubleRotateLR(TreeNode* &k3)
{
SingRotateRight(k3->lson);
SingRotateLeft(k3);
}
//右左情况的旋转
template
void AVLTree::DoubleRotateRL(TreeNode* &k3)
{
SingRotateLeft(k3->rson);
SingRotateRight(k3);
}
//插入
template
int AVLTree::insertpri(TreeNode* &node,T x)
{
int tmp1 =0,tmp2=0;
bool brotate = false;
if(node==NULL)//如果当前节点为空，加入该节点
{
node=new TreeNode();
node->data=x;
node->hgt++;
cout<<"nodea"<data<<"height"<hgt<data>x)//如果x小于节点的值,就继续在节点的左子树中插入x
{
tmp1=insertpri(node->lson,x);
if(tmp1 == 1)
{
node->hgt++;
cout<<"nodeb"<data<<"height"<hgt<lson)-height(node->rson))
{
brotate = true;
if(xlson->data)
{
cout<<"ll"<datarson,x);
if(tmp2 == 1)
{
node->hgt++;
cout<<"nodec"<data<<"height"<hgt<rson)-height(node->lson))
{
if(x>node->rson->data)
{
cout<<"rr"<freq);//如果相等,就把频率加1，但是有个问题沿途遇到的节点加1了，但是其他的就没有，所以会导致有重复数据时候错误和乱套
cout<<"nodee"<data<<"freq"<freq<hgt=Max(height(node->lson),height(node->rson))+1;//更新存在左右子树的根节点的高度
if(tmp1 || tmp2)
{
return 1;
}
return 0;
}
//插入接口
template
void AVLTree::insert(T x)
{
insertpri(root,x);
}
template
void AVLTree::InorderBST(TreeNode* node)
{//以中序方式遍历二叉排序树T，并显示
if(node!=NULL)
{
cout<data;
if(node->lson!=NULL||node->rson!=NULL)
{
cout<<"(";
InorderBST(node->lson);//递归调用中序遍历函数
if(node->rson!=NULL)
cout<<",";
InorderBST(node->rson); //递归调用中序遍历函数
cout<<")";
}
}
}
template
void AVLTree::print()
{
InorderBST(root);
}
//查找
template
TreeNode* AVLTree::findpri(TreeNode* node,T x)
{
if(node==NULL)//如果节点为空说明没找到,返回NULL
{
return NULL;
}
if(node->data>x)//如果x小于节点的值,就继续在节点的左子树中查找x
{
return findpri(node->lson,x);
}
else if(node->datarson,x);
}
else return node;//如果相等,就找到了此节点
}
//查找接口
template
TreeNode* AVLTree::find(T x)
{
return findpri(root,x);
}
//删除
template
int AVLTree::Deletepri(TreeNode* &node,T x)
{
int tmp1=0,tmp2 = 0;
if(node==NULL)
{
return 0 ;//没有找到值是x的节点
}
if(x < node->data)
{
//如果x小于节点的值,就继续在节点的左子树中删除x
tmp1 = Deletepri(node->lson,x);
if(tmp1==1)
{
node->hgt--;
//找到节点node，返回上一层
if(2==height(node->lson)-height(node->rson))//平衡因子定义为右儿子高度减去左儿子的高度
{
//注意 需要考虑节点node->lson->rson==NULL的情况，这个时候求height是会挂掉的
if((node->lson->rson!=NULL&&(height(node->lson->rson)>height(node->lson->lson))) || (node->lson->rson==NULL&&height(node->lson->rson)>0) )
{
cout<<"lr"< node->data)
{
tmp2 = Deletepri(node->rson,x);//如果x大于节点的值,就继续在节点的右子树中删除x
if(tmp2==1)
{
node->hgt--;
if(2==height(node->rson)-height(node->lson))
{
if((node->rson->lson!=NULL&&(height(node->rson->lson)>height(node->rson->rson))) || (node->rson->lson==NULL&&height(node->rson->lson)>0) )
{
cout<<"rl"<lson&&node->rson)//此节点有两个儿子
{
TreeNode* temp=node->rson;//temp指向节点的右儿子
while(temp->lson!=NULL) temp=temp->lson;//找到右子树中值最小的节点
//把右子树中最小节点的值赋值给本节点
node->data=temp->data;
node->freq=temp->freq;
Deletepri(node->rson,temp->data);//删除右子树中最小值的节点
if(2==height(node->lson)-height(node->rson))
{
if(node->lson->rson!=NULL&& (height(node->lson->rson)>height(node->lson->lson) ))
{
cout<<"equal lr"<* temp=node;
TreeNode* nonenullnode=NULL;
if(node->lson==NULL)//有右儿子或者没有儿子
{
node=node->rson;
}
else if(node->rson==NULL)//有左儿子
{
node=node->lson;
}
delete(temp);
temp=NULL;
}
return 1;
}
//if(node==NULL) return 0;
node->hgt=Max(height(node->lson),height(node->rson))+1;
if(tmp1 || tmp2)
{
return 1;
}
else return 0;
}
//删除接口
template
void AVLTree::Delete(T x)
{
Deletepri(root,x);
}
//中序遍历函数
template
void AVLTree::insubtree(TreeNode* node)
{
if(node==NULL) return;
insubtree(node->lson);//先遍历左子树
cout<data<<" ";//输出根节点
insubtree(node->rson);//再遍历右子树
}
//中序遍历接口
template
void AVLTree::traversal()
{
insubtree(root);
}
int main()
{
const int n =5;
int a[n] = {4,2,6,5,8};
AVLTree btree;
for(int i =0; i btree2;
for(int i =0; i btree3;
for(int i =0; i