torch.nn.MaxPool1d各参数分析

一、官方定义和参数解释

官方文档: https://pytorch.org/docs/stable/generated/torch.nn.MaxPool1d.html?highlight=maxpool1d#torch.nn.MaxPool1d.
翻到最下面对于输入和输出维度的解释为：

• Input： $(N,C,L_{in})$ or $(C,L_{in})$

• Output：$(N,C,L_{out})$ or $(C,L_{out})$, where
  $$L_{out}=\lfloor \frac{L_{in}+2\times padding-dilation\times (kernel\_size-1)-1}{stride}+1\rfloor$$

• kernel_size – The size of the sliding window, must be > 0.

• stride – The stride of the sliding window, must be > 0. Default value is kernel_size.

• padding – Implicit negative infinity padding to be added on both sides, must be >= 0 and <= kernel_size / 2.

• dilation – The stride between elements within a sliding window, must be > 0.

• return_indices – If True, will return the argmax along with the max values. Useful for torch.nn.MaxUnpool1d later

• ceil_mode – If True, will use ceil instead of floor to compute the output shape. This ensures that every element in the input tensor is covered by a sliding window.

1.1 初步解释各个参数

• kernel_size – 池化窗口的size（大小），也就是这个窗口包含的元素个数，必须>0

• stride – 滑动的池化窗口的stride（跨步），必须 > 0，默认值等于kernel_size

• padding – 直观翻译就是填充个数，在both sides（双侧）隐式地添加的填充元素（填充值是负无穷，即$-\infty$，这样填充不会让最大池化结果出现新的元素值，因为没有元素值会比负无穷更小），该填充个数必须>= 0 且 <= kernel_size / 2.

• dilation – 在滑动池化窗口内部（注意是within），元素之间的stride（跨步），必须> 0.

• return_indices – 直观翻译是返回索引。如果值为True，会在返回最大池化结果（就是求出的最大值max values）的同时返回对应元素的索引（argmax ）。对于后续调用torch.nn.MaxUnpool1d的时候很有用。

• ceil_mode – 直观翻译就是顶层模式。如果值为True，会在计算输出shape的时候一直触碰到顶层天花板（ceil），而不是保底取底（floor）。这样能够保证输入的tensor中的每个元素都能被滑动窗口cover到。

二、用代码测试各个参数的影响

2.1 kernel_size、stride和ceil_mode画图分析

首先创建池化对象的时候，指定kernel_size、stride并用一个长度为10的数组测试结果，分析这两个参数的作用。
由于官方文档指定了输入的维度必须是$(N,C,L_{in})$或者$(C,L_{in})$，而池化只对最后一个维度$L_{in}$（长度length）进行操作，对$N$（样本个数number）、$C$（通道维度channel）这两个维度不造成影响，因此方便起见只设置一个二维的Tensor，它的shape为$(C=2,L_{in}=10)$，重点关注$L_{in}$=10情况下的池化过程。

# 测试kernel_size和stride
import torch
m = nn.MaxPool1d(3, stride=2)
input = torch.Tensor([[1,2,3,4,5,6,7,8,9,10],[1,2,3,4,5,6,7,8,9,10]])
output = m(input)
# 交互模式下查看输入输出的维度，以及池化结果
In[21]: input.shape
Out[21]: torch.Size([2, 10])
In[22]: output.shape
Out[22]: torch.Size([2, 4])
In[23]: output
Out[23]: 
tensor([[3., 5., 7., 9.],
        [3., 5., 7., 9.]])

对于1维池化，池化维度可看作一行长度为$L_{in}$的躺平的一维数组。
首先，把input的第二维度画出来，就是一个躺平的一维数组，元素值从1到10，由下图所示。

具体池化操作总共计算了4次：

1. 从左到右，构建一个长度为3的窗口，首先cover的三个元素是1、2、3，得到一个最大值为3。
2. 然后向右移动窗口，移动2步，也就是stride=2（从起始位置1移动到3），cover三个元素变成了3、4、5，得到一个最大值为5。
3. 再次移动窗口得到最大值7。
4. 再然后得到最大值9。

此时窗口已经不能再往后移动（再移动的话，从9开始cover的元素不够3个，就超边界了），因此pool结束，返回4个结果值[3, 5, 7, 9]，与程序输出的output相符合。

2.1.1 ceil_mode池化过程推测

注： 从这里看出，元素10就因为是保底模式（floor）而没有被窗口cover到。如果设置ceil模式为True，得到结果是[3, 5, 7, 9, 10]，读者可以自行验证。从这个结果来揣测，可猜出ceil模式的意思是窗口会保证右边界能一直移动到ceil元素（最顶端的那些个元素，天花板一样的存在），在这个例子下就是在窗口cover到元素7、8、9并计算出最大值9以后，探测到还有个顶端元素10没被cover，因此自动往右移动1步，cover住元素8、9、10再计算出一个最大值10。

2.1.2 padding、dilation、ceil_mode的默认值

另外： 在pycharm的console交互模式下能看到m = nn.MaxPool1d(3, stride=2)代码执行后m对象的其他未指定参数的默认值：填充个数padding默认为0，窗口内部跨步长度dilation默认为1，ceil_mode默认是False，如下图所示。

2.1.3 stride的默认值

如果只设置必要的参数，即执行的是m = nn.MaxPool1d(3)，只设置窗口大小kernel_size=3，则跨步长度stride默认值等于窗口大小，也为3，如下图所示。

2.1.4 代入公式计算$L_{out}$理论值

代入公式计算$L_{out}$理论值： 将$L_{in}$=10, kernel_size=3, stride=2, padding=0, dilation=1代入官方文档给出的公式，计算得到池化操作后输出的维度$L_{out}=\lfloor (10+0-2-1)/2+1\rfloor =\lfloor 4.5\rfloor =4$，与程序输出的output.shape$(C=2,L_{out}=4)$一致。

2.1.5 kernel_size、stride、ceil_mode作用总结

结论：

• kernel_size（窗口大小）就是窗口cover的元素个数，创建MaxPool1d对象时必须指定该参数
• stride（窗口滑动跨步长度）是每次窗口往后移动几格，默认值等于kernel_size
• ceil_mode（是否滑到最顶端元素）默认值为False。默认情况下，窗口有可能因为剩余元素不足kernel_size个而不再cover剩余的元素，而如果设置ceil_mode为True则能够保证窗口继续cover剩余未访问到的顶层元素。

2.2 dilation画图分析

# 测试dilation
import torch
m = nn.MaxPool1d(3, stride=2, dilation=2)
input = torch.Tensor([[1,2,3,4,5,6,7,8,9,10],[1,2,3,4,5,6,7,8,9,10]])
output = m(input)
# 交互模式下查看输入输出的维度，以及池化结果
In[21]: input.shape
Out[21]: torch.Size([2, 10])
In[22]: output.shape
Out[22]: torch.Size([2, 3])
In[23]: output
Out[23]: 
tensor([[5., 7., 9.],
        [5., 7., 9.]])

这次在原来基础上，设置dilation=2。从返回结果[5, 7, 9]进行揣测，第一次池化窗口肯定覆盖且最多覆盖到了元素5，才会先计算出5是最大值。

那怎么在窗口大小kernel_size=3（窗口只包含3个元素）情况下第一次（从最左端的元素1开始）就cover到元素5（窗口的右边界一定到元素5为止）那个位置？

那只能推测出一个事实：这个窗口是不连续的，跳着cover了三个元素，如下图所示。

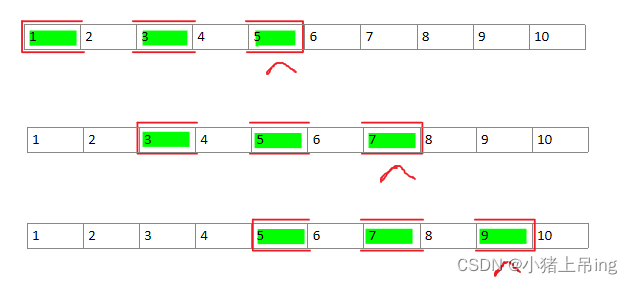
具体池化操作总共计算了3次：

1. 从左到右，构建一个长度为3的不连续 窗口，窗口内部的前一个元素和下一个元素之间跨步dilation=2（例如元素1的下一个是元素3）。首先cover的三个元素是1、3、5，得到一个最大值为5。
2. 然后向右移动窗口，移动2步，也就是stride=2（从起始位置1移动到3），cover三个元素变成了3、5、7，得到一个最大值为7。
3. 再次移动窗口到元素5，cover元素5、7、9，得到最大值9。

2.2.1 代入公式计算$L_{out}$理论值

代入公式计算$L_{out}$理论值： 将$L_{in}$=10, kernel_size=3, stride=2, padding=0, dilation=2代入官方文档给出的公式，计算得到池化操作后输出的维度$L_{out}=\lfloor (10+0-2\times 2-1)/2+1\rfloor =\lfloor 3.5\rfloor =3$，与程序输出的output.shape$(C=2,L_{out}=3)$一致。

2.2.2 dilation作用总结

结论：

• dilation（窗口内元素间跨步长度）就是窗口内部前后元素的跨步，默认值为1，此时窗口内的元素是连续的、相连紧挨着的。如果>1的话窗口就是不连续的，cover的元素是跳着的（间隔着的）。

2.3 padding画图分析

# 测试padding
import torch
m = nn.MaxPool1d(3,stride=2,padding=1,dilation=2)
input = torch.Tensor([[1,2,3,4,5,6,7,8,9,10],[1,2,3,4,5,6,7,8,9,10]])
output = m(input)
# 交互模式下查看输入输出的维度，以及池化结果
In[21]: input.shape
Out[21]: torch.Size([2, 10])
In[22]: output.shape
Out[22]: torch.Size([2, 4])
In[23]: output
Out[23]: 
tensor([[ 4.,  6.,  8., 10.],
        [ 4.,  6.,  8., 10.]])

这次在原来基础上，设置padding=1（填充1个负无穷元素）。从返回结果[4, 6, 8, 10]进行揣测，第一次池化窗口肯定覆盖且最多覆盖到了元素4，才会先计算出4是最大值。

而且由于dilation=2，元素是隔一个cover的，从最右端元素4往前推，推够3个元素为止，可揣测出第一次窗口cover的元素是？、2、4。而？只可能是填充的那个负无穷元素，如下图所示。

具体池化操作总共计算了4次：

1. 在左边填充一个$-\infty$元素。首先cover的三个元素是$-\infty$、2、4，得到一个最大值为4。
2. 然后向右移动窗口，移动2步，也就是stride=2（从起始位置1移动到3），cover三个元素变成了2、4、6，得到一个最大值为6。
3. 再次移动窗口得到最大值8。
4. 再然后得到最大值10。

2.3.1 代入公式计算$L_{out}$理论值

代入公式计算$L_{out}$理论值： 将$L_{in}$=10, kernel_size=3, stride=2, padding=1, dilation=2代入官方文档给出的公式，计算得到池化操作后输出的维度$L_{out}=\lfloor (10+2\times 1-2\times 2-1)/2+1\rfloor =\lfloor 4.5\rfloor =4$，与程序输出的output.shape$(C=2,L_{out}=4)$一致。

2.3.2 padding作用总结

结论：

• padding（填充元素个数）。默认值为0（不填充）且值不能超过kernel_size/2（向下取值）。padding=1的时候是在窗口左端填充一个$-\infty$元素。如果设置为2，在本例子中会报错提示 “RuntimeError: max_pool1d() padding should be at most half of kernel size, but got padding=2 and kernel_size=3” ，padding的值不能超过3/2=1（1.5向下取值为1），所以padding只能取1了。读者可以自行尝试m = nn.MaxPool1d(4,padding=2)的情况下，填充的两个元素是均在左侧添加还是一左一右。

到这里，一维池化的5个参数的默认值、对池化过程的影响分析完毕。二维甚至更高维的池化参数的理解应该可以类推。

torch.nn.MaxPool1d和torch.max的区别

torch.max是直接在某一维度上取这一行元素的最大值。
torch.nn.MaxPool1d是在某一维度上用滑动窗口以某种跳步取最大池化，确实窗口长度=列表长度、其他参数默认的情况下池化计算的结果与torch.max相同，但是未免太大材小用，杀鸡牛刀。
举例观察：

import torch
test = torch.Tensor([[1,3,5,4,2,8,7,6],[1,3,5,4,2,8,7,6]]).view(2,2,4)
# tensor([[[1., 3., 5., 4.],
#          [2., 8., 7., 6.]],
# 
#         [[1., 3., 5., 4.],
#          [2., 8., 7., 6.]]])
# torch.Size([2, 2, 4])

#----用torch.nn.MaxPool1d求最大值
m = torch.nn.MaxPool1d(test.size()[2])
output = m(test)
In[21]: output
Out[21]:
tensor([[[5.],
         [8.]],
        [[5.],
         [8.]]])
In[22]: output.size()
Out[22]:
torch.Size([2, 2, 1])

#----用torch.max求最大值
output2 = torch.max(test,2,keepdim=True)[0]
In[23]: output2
Out[23]:
tensor([[[5.],
         [8.]],
        [[5.],
         [8.]]])
In[24]: output2.size()
Out[24]:
torch.Size([2, 2, 1])
In[25]: torch.equal(output,output2)
Out[25]:True