机器学习基础知识总结
机器学习
-
- 一、回归
-
- 1、普通线性回归
- 2、回归评估指标
- 3、岭回归
- 4、LASSO回归
- 5、弹性网络
- 6、逻辑斯蒂回归
- 7、贝叶斯岭回归
- 8、核岭回归
- 9、SVR
- 二、分类
-
- 1、k近邻
- 2、分类指标
- 3、SVM
- 三、数据预处理
- 四、决策树与回归树
-
- 1、决策树
- 2、回归树
- 3、集成学习
- 五、聚类
-
- 1、Kmeans
- 2、Kmeans++
- 3、MeanShift(均值迁移)
- 4、层次聚类
- 5、密度聚类
- 6、混合高斯
- 7、聚类衡量指标
- 8、聚类代码实现
- 六、降维
-
- 1、主成分分析(PCA)
- 2、线性判别分析(LDA)
一、回归
1、普通线性回归
只能处理线性问题,对异常数据敏感,不稳定,当w过大时,x有微小变化时,会引起y产生较大的变化,因此需要对w进行控制
y ^ ( w , x ) = w 0 + w 1 x 1 + . . . + w p x p \hat{y}(w,x)=w_{0} +w_{1}x_{1}+...+w_{p}x_{p} y^(w,x)=w0+w1x1+...+wpxp
损失函数: min w ∥ X w − y ∥ 2 2 \underset{w}{\min}\|Xw-y\|_{2}^{2} wmin∥Xw−y∥22
2、回归评估指标
(1)平均绝对误差 MAE
(2)平均方差 MSE
(3)可解释方差 EVS
(4)r2_score:越接近于1越好
3、岭回归
参数w过大时,会出现过拟合,因此在线性回归的基础上加入L2正则化
L2正则化的函数图像是一个圆,等值线与L2图像相交时使得w1或w2等于0的机率小了许多,L2正则化能使不重要的权重变小,主要用于防止模型过拟合。
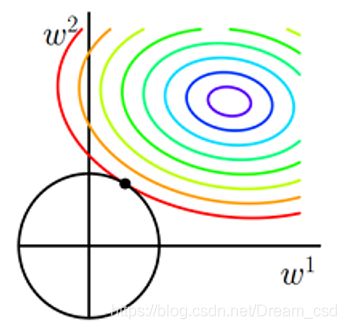
min w ∥ X w − y ∥ 2 2 + α ∥ w ∥ 2 2 \underset{w}{\min}\|Xw-y\|_{2}^{2}+\alpha \|w\|_{2}^{2} wmin∥Xw−y∥22+α∥w∥22
4、LASSO回归
加入L1正则化
黑色菱形就是L1正则化函数,当等值线与正则化函数图像首次相交的地方就是最优解,因为L1损失函数在多维情况下会有更多的角,因此等值线与这些角相交的几率更大,所以L1正则化会使不重要的权重直接变为0,L1正则化可以产生更稀疏的权值矩阵,可以用于特征选择,同时一定程度上防止过拟合;系数α可以控制正则化函数,当α越小时,函数图像越大,反之,函数图像越小。
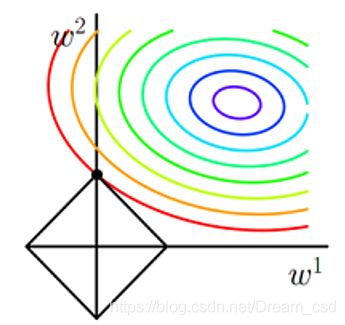
min w 1 2 n ∥ X w − y ∥ 2 2 + α ∥ w ∥ 1 \underset{w}{\min}\frac{1}{2n}\|Xw-y\|_{2}^{2}+\alpha \|w\|_{1} wmin2n1∥Xw−y∥22+α∥w∥1
5、弹性网络
将岭回归和LASSO回归进行结合,同时加入L1和L2正则化
min w 1 2 n ∥ X w − y ∥ 2 2 + α ρ ∥ w ∥ 1 + α ( 1 − ρ ) 2 ∥ w ∥ 2 2 \underset{w}{\min}\frac{1}{2n}\|Xw-y\|_{2}^{2}+\alpha \rho \|w\|_{1}+\frac{\alpha(1-\rho)}{2} \|w\|_{2}^{2} wmin2n1∥Xw−y∥22+αρ∥w∥1+2α(1−ρ)∥w∥22
6、逻辑斯蒂回归
用来做分类,对输出进行sigmoid激活,同时加入了L1和L2正则化
7、贝叶斯岭回归
L2正则化是由假设w服从标准正态分布由贝叶斯方程推断而来,L1正则化是由假设w服从拉普拉斯分布由贝叶斯方程推断而来。
以上各种回归的python代码
from sklearn import linear_model
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error,mean_squared_error,r2_score,explained_variance_score
np.random.RandomState(0)
x,y = datasets.make_regression(n_samples=100,n_features=1,n_targets=1,noise=10)
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.3)
reg = linear_model.LinearRegression()#普通线性回归
# reg = linear_model.Ridge(0.5)#岭回归
# reg = linear_model.Lasso(0.1)#LASSO回归
# reg = linear_model.ElasticNet(0.5,0.5)#弹性网络
# reg = linear_model.LogisticRegression()#逻辑斯蒂回归,用于二分类
# reg = linear_model.BayesianRidge()#贝叶斯岭回归
reg.fit(x_train,y_train)
# print(reg.coef_,reg.intercept_)#模型的参数,coef相当于斜率,intercept相当于截距b
y_predict = reg.predict(x_test)
#平均绝对误差
print(mean_absolute_error(y_test,y_predict))
#均方误差
print(mean_squared_error(y_test,y_predict))
#R2分数
print(r2_score(y_test,y_predict))
#可解释方差
print(explained_variance_score(y_test,y_predict))
_x = np.array([-2.5,2.5])
_y = reg.predict(_x[:,None])
plt.scatter(x_test,y_test)
plt.plot(_x,_y,linewidth = 3,color = 'red')
plt.show()
8、核岭回归
核函数:线性核linear;多项式核;径向基rbf;sigmoid核
from sklearn.kernel_ridge import KernelRidge
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import GridSearchCV
rng = np.random.RandomState(0)
x = 5*rng.rand(100,1)
y = np.sin(x).ravel()#ravel():将多维数组转换为一维数组
#添加噪音
y[::5] += 3*(0.5-rng.rand(x.shape[0]//5))
# kr = KernelRidge(kernel = 'sigmoid',gamma=0.4)
#polynomial多项式,logspace(a,b,n)把10的a次方到10的b次方分为n份
#调参利器
kr = GridSearchCV(KernelRidge(),
param_grid={'kernel':['rbf','laplacian','polynomial','sigmoid'],
'alpha':[1e0,0.1,0.01,1e-3],
'gamma':np.logspace(-2,2,5)})
kr.fit(x,y)
print(kr.best_score_,kr.best_params_)
x_plot = np.linspace(0,5,100)
y_kr = kr.predict(x_plot[:,None])
plt.scatter(x,y)
plt.plot(x_plot,y_kr)
plt.show()
9、SVR
求得一个超平面,使得两个支持向量机之间的宽度最小,也就是集合中的所有数据到该平面的距离最近。
传统回归需要预测值与实际值相等时为预测正确,而SVR要求预测值于实际值之差在 ε \varepsilon ε之内即为预测正确。
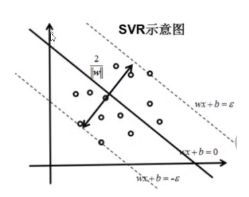
损失函数: m a x 1 2 ∥ w ∥ 2 + λ ( ∣ y i − ( w x i + b ) ∣ − ε ) max\frac{1}{2}\|w\|^{2}+\lambda (|y_{i}-(wx_{i}+b)|-\varepsilon ) max21∥w∥2+λ(∣yi−(wxi+b)∣−ε)
二、分类
1、k近邻
原理:对数据进行分类,以该数据为中心画圈,圈中包含的数据哪个分类数量占比多,该数据就属于哪个类别。
KD-TREE:kd树是二叉树的变种,
当它的左子树不为空时,左子树上所有节点的值均小于它根结点的值;
当它的右子树不为空时,右子树上所有节点的值均大于它根结点的值;
它的左、右子树也分别为二叉树
建立kd树:对于二维数据,计算两个方向上的方差,按照方差最大的维度对数据进行排序,选取中值对数据进行划分,划分后的两部分数据再计算方差,重复上述操作,直到数据划分完为止。
数据查找:根据建立的kd树,按照划分数据时的方差,找到临近的叶子节点,然后以该数据为中心,以该数据到叶子节点数据的距离为半径画圆,如果该圆内不含有其它节点,则该数据离此叶子节点最近;如果该圆内包含其它叶子节点,此节点需要回溯叶子节点的父节点和该父节点的另外一个子节点,计算它们之间的距离,找到距离最近的点,然后在以最近的点为半径画圆,如果该圆内无其它点,则判断该数据与此节点距离最近,否则需要继续回溯。
2、分类指标
(1)混淆矩阵:
| 预测情况P or N | 实际label为1,预测对了为T | 实际label为0,预测对了为T |
|---|---|---|
| 预测为正例1,P | TP(预测为1,实际为1) | FP(预测为1,实际为0) |
| 预测为负例0,N | FN(预测为0,实际为1) | TN(预测为0,实际也为0) |
(2)查准率(Precision)、查全率(Recall)和F1-score:
查准率(Precision)=TP/(TP+FP);预测出的阳性样本中正确的有多少
查全率(Recall)=TP/(TP+FN);正确预测为阳性的数量占总样本中阳性数量的比例
F 1 = 2 ∗ P ∗ R P + R = 2 T P 2 T P + F N + F P F_{1}=2\ast \frac{P\ast R}{P+R}=\frac{2TP}{2TP+FN+FP} F1=2∗P+RP∗R=2TP+FN+FP2TP
(3)P-R曲线
将样本按照按照预测为正例的概率值从大到小进行排序,从第一个开始,逐个将当前样本点的预测值设置为阈值,有了阈值之后,即可得出混淆矩阵各项的数值,然后计算出P和R,以R为横坐标,P为纵坐标,绘制于图中,即可得出P-R曲线
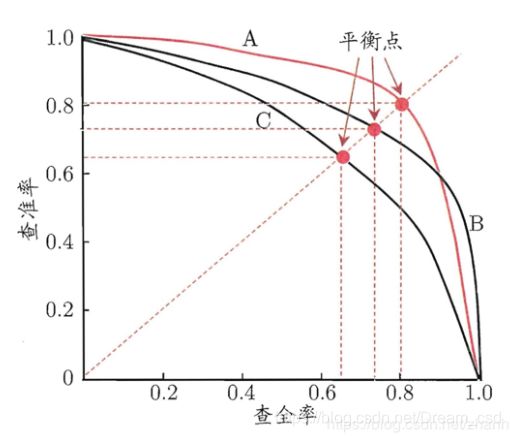
曲线下方的面积表示AP值,对所有类别AP值求平均后就是mAP值
(4)虚警率(False Positive Rate)和真正率(True Positive Rate):
T P R = T P T P + F N , F P R = F P F P + T N TPR = \frac{TP}{TP+FN} ,FPR = \frac{FP}{FP+TN} TPR=TP+FNTP,FPR=FP+TNFP
(5)ROC曲线:
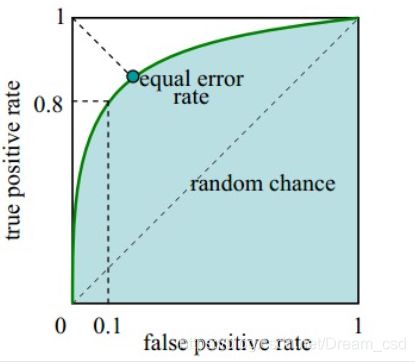
ROC曲线越接近左上角,该分类器的性能越好,ROC曲线所覆盖的面积称为AUC,AUC越大性能越好。
3、SVM
寻找区分两个类别并且使两个支撑向量之间距离最大的超平面
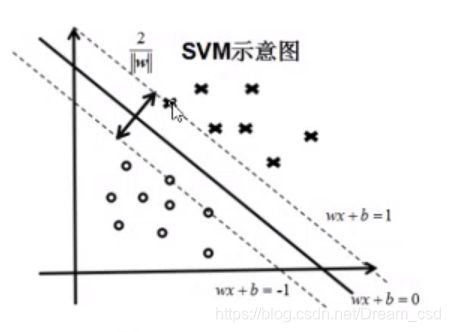
损失函数: m i n 1 2 ∥ w ∥ 2 + λ ( 1 − ∣ y i − ( w x i + b ) ∣ ) min\frac{1}{2}\|w\|^{2}+\lambda (1-|y_{i}-(wx_{i}+b)| ) min21∥w∥2+λ(1−∣yi−(wxi+b)∣)
SVM学习问题可以表示为凸优化问题,因此可以利用已知的有效算法发现目标函数的全局最小值
三、数据预处理
(1)标准化:去均值、方差规模化
将特征数据的分布调整为标准正态分布
scaler = preprocessing.StandardScaler()
x_scale = scaler.fit_transform(x)
print(x_scale)
print(x_scale.mean(axis=0),x_scale.std(0))
(2)MinMaxScaler
x = x − x . m i n ( a x i s = 0 ) x . m a x ( a x i s = 0 ) − x . m i n ( a x i s = 0 ) x=\frac{x-x.min(axis=0)}{x.max(axis=0)-x.min(axis=0)} x=x.max(axis=0)−x.min(axis=0)x−x.min(axis=0)
scaler = preprocessing.MinMaxScaler()
x_scale = scaler.fit_transform(x)
print(x_scale)
print(x_scale.mean(axis=0),x_scale.std(0))
(3)MaxAbsScaler
适用于稀疏矩阵,矩阵中0较多
x = x ∣ x ∣ . m a x ( a x i s = 0 ) x=\frac{x}{|x|.max(axis=0)} x=∣x∣.max(axis=0)x
scaler = preprocessing.MaxAbsScaler()
x_scale = scaler.fit_transform(x)
print(x_scale)
print(x_scale.mean(0),x_scale.std(0))
(4)RobustScaler
x=(x-mean)/std,其中mean和std为x所在列的均值和标准差,不适用稀疏矩阵,适用于数据异常值较多的情况
scaler = preprocessing.RobustScaler()
x_scale = scaler.fit_transform(x)
print(x_scale)
print(x_scale.mean(0),x_scale.std(0))
(5)Normalization(正则化)
scaler = preprocessing.Normalizer(norm='l2')
x_scale = scaler.fit_transform(x)
print(x_scale)
(6)二值化
将数值型的特征数据转化为布尔型的值
scaler = preprocessing.Binarizer(threshold=0)#小于阈值归为0,否则归为1
x_scale = scaler.fit_transform(x)
print(x_scale)
(7)OneHotEncoder独热编码
对于离散型数据分类的标签应该用onehot
enc = preprocessing.OneHotEncoder(n_values=3,sparse=False)
ans = enc.fit_transform([[0],[1],[2],[1]])
compile(ans)
(8)弥补缺失数据
弥补缺失数据可以使用均值
中位数、众数等
imp = preprocessing.Imputer(missing_values='NaN', strategy='mean', axis=0)
#直接补值,np.nan代表缺失数据
y_imp = imp.fit_transform([[np.nan, 2], [6, np.nan], [7, 6]])
print(y_imp)
#通过学习补值
imp.fit([[1, 2], [np.nan, 3], [7, 6]])
y_imp = imp.transform([[np.nan, 2], [6, np.nan], [7, 6]])
print(y_imp)
四、决策树与回归树
1、决策树
决策树是一种分而治之的决策过程。一棵决策树的生成过程主要分为下3个部分:
1、特征选择:从训练数据中众多的特征中选择一个特征作为当前节点的分裂标准,如何选择特征有着很多不同量化评估标准,从而衍生出不同的决策树算法。
2、决策树生成:根据选择的特征评估标准,从上至下递归地生成子节点,直到数据集不可分则决策树停止生长。树结构来说,递归结构是最容易理解的方式。
3、剪枝:决策树容易过拟合,一般来需要剪枝,缩小树结构规模、缓解过拟合。剪枝技术有预剪枝和后剪枝两种。
(1)熵:随机变量不确定性的度量
定义:假设随机变量X的可能取值有 x 1 , x 2 , . . . , x n x_{1},x_{2},...,x_{n} x1,x2,...,xn,对于每一个可能的取值 x i x_{i} xi,其概率为 P ( X = x i ) = p i , i = 1 , 2... , n P(X=x_{i})=p_{i},i=1,2...,n P(X=xi)=pi,i=1,2...,n。随机变量的熵为:
H ( X ) = − ∑ i = 1 n p i l o g 2 p i H(X)=-\sum_{i=1}^{n}p_{i}log_{2}p_{i} H(X)=−i=1∑npilog2pi
(2)条件熵:
设有随机变量(X,Y),条件熵H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性。
H ( Y ∣ X ) = ∑ i = 1 n p i H ( Y ∣ X = x i ) H(Y|X)=\sum _{i=1}^{n}p_{i}H(Y|X=x_{i}) H(Y∣X)=∑i=1npiH(Y∣X=xi)
p i = P ( X = x i ) , i = 1 , 2 , . . . , n p_{i}=P(X=x_{i}), i=1,2,...,n pi=P(X=xi),i=1,2,...,n
(3)信息增益:
信息增益表示得知特征X的信息而使得Y的信息不确定性减少的程度。 假设划分前样本集合D的熵为H(D)。使用某个特征A划分数据集D,计算划分后的数据子集的熵为H(D|A), 则信息增益为:
g ( D , A ) = H ( D ) − H ( D ∣ A ) g(D,A)=H(D)-H(D|A) g(D,A)=H(D)−H(D∣A)
对于样本集合,假设样本有k个类别,每个类别的概率为 ∣ C k ∣ ∣ D ∣ \frac{|C_{k}|}{|D|} ∣D∣∣Ck∣,其中 ∣ C k ∣ ∣ D ∣ {|C_{k}|}{|D|} ∣Ck∣∣D∣为类别为k的样本个数, ∣ D ∣ |D| ∣D∣为样本总数。样本集合D的熵为:
H ( D ) = − ∑ k = 1 k ∣ C k ∣ ∣ D ∣ l o g 2 ∣ C k ∣ ∣ D ∣ H(D)=-\sum_{k=1}^{k}\frac{|C_{k}|}{|D|}log_{2}\frac{|C_{k}|}{|D|} H(D)=−k=1∑k∣D∣∣Ck∣log2∣D∣∣Ck∣
条件熵: H ( D ∣ A ) = − ∑ i = 1 n ∣ D i ∣ ∣ D ∣ ∑ k = 1 k ∣ D i k ∣ ∣ D i ∣ l o g 2 ∣ D i k ∣ ∣ D i ∣ H(D|A)=-\sum_{i=1}^{n}\frac{|D_{i}|}{|D|}\sum_{k=1}^{k}\frac{|D_{ik}|}{|D_{i}|}log_{2}\frac{|D_{ik}|}{|D_{i}|} H(D∣A)=−i=1∑n∣D∣∣Di∣k=1∑k∣Di∣∣Dik∣log2∣Di∣∣Dik∣
注:在决策树构建的过程中我们总是希望集合往最快到达纯度更高的子集合方向发展,因此我们总是选择使得信息增益最大的特征来划分当前数据集D。
(4)信息增益率:
特征A对训练集D的信息增益率 g R ( D , A ) g_{R}(D,A) gR(D,A)定义为其信息增益与训练集D关于特征值A的熵 H A ( D ) H_{A}(D) HA(D)之比:
g R ( D , A ) = g ( D , A ) H A ( D ) g_{R}(D,A)=\frac{g(D,A)}{H_{A}(D)} gR(D,A)=HA(D)g(D,A)
注:信息增益率偏向于取值较少的特征,特征较少时 1 H A ( D ) \frac{1}{H_{A}(D)} HA(D)1较大,信息增益率较大;相反信息增益会偏向于取值较多的特征。
(5)基尼指数:
基尼指数Gini(D)表示集合D的不确定性,基尼指数取值[0,1]之间,值越小样本不确定性越小,被分错的概率越小,纯度越高。
G i n i ( p ) = 1 − ∑ k = 1 k p k 2 Gini(p)=1-\sum_{k=1}^{k}p_{k}^{2} Gini(p)=1−k=1∑kpk2
(6)决策树生成:
| 生成算法 | 划分标准 |
|---|---|
| ID3 | 信息增益 |
| C4.5 | 信息增益率 |
| CART(二叉树) | 基尼指数 |
(7)剪枝:
max_depth:限制树的最大深度,超过设定深度的树枝全部剪掉
min_samples_leaf:一个节点在分枝后每个子节点必须包含至少min_samples_leaf个训练样本,否则分支不会发生
min_samples_split:一个节点必须要包含至少min_samples_split个训练样本,才允许被分支
max_features:限制分枝时考虑的特征个数,超过限制的特征个数会被舍弃
min_impurity_decrease:限制信息增益的大小
(8)python代码:
from sklearn import datasets,preprocessing,tree
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
import graphviz
wine = datasets.load_wine()
x,y = wine.data,wine.target
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.3)
scaler = preprocessing.StandardScaler().fit(x_train)
x_train = scaler.transform(x_train)
x_test = scaler.transform(x_test)
model = tree.DecisionTreeClassifier()
model.fit(x_train,y_train)
y_pred = model.predict(x_test)
#查看特征权重
print(wine.feature_names)
print(model.feature_importances_)
#评估
print(accuracy_score(y_test,y_pred))
# dtModel:决策树模型
# out_file:图形数据的输出路径
# class_names:目标属性的名称,
# feature_names:特征属性的名称
# filled= True :是否使用颜色填充
# rounded=True:边框是否采用圆角边框
# special_characters: 是否有特殊字符
dot_data = tree.export_graphviz(model,feature_names=iris.feature_names,
class_names=iris.target_names,
filled=True,rounded=True,
special_characters=True)
graph = graphviz.Source(dot_data)
graph.render('iris')
2、回归树
原理:对于一组数据,将数据进行切分成两份,分别计算平均值,再根据均值算出两组数据的方差,按照方差最小的对数据进行划分,以此类推直到数据分完为止。
代码:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
from sklearn import linear_model
x = np.array(list(range(1,11))).reshape(-1,1)
y = np.array([5.56, 5.70, 5.91, 6.40, 6.80, 7.05, 8.90, 8.70, 9.00, 9.05]).ravel()
#创建并训练模型
model1 = DecisionTreeRegressor(max_depth=1)
model2 = DecisionTreeRegressor(max_depth=3)
model3 = linear_model.LinearRegression()
model1.fit(x,y)
model2.fit(x,y)
model3.fit(x,y)
#预测
x_test = np.arange(0.0,10.0,0.01)[:,np.newaxis]#np.newaxis:增加一个新维度
y_1 = model1.predict(x_test)
y_2 = model2.predict(x_test)
y_3 = model3.predict(x_test)
#打印结果
plt.scatter(x,y,s = 20,c = "darkorange",label = 'data')
plt.plot(x_test,y_1,color = "cornflowerblue",label = 'max_depth = 1',linewidth = 2)
plt.plot(x_test,y_2,color = "yellowgreen",label = 'max_depth = 3',linewidth = 2)
plt.plot(x_test,y_3,color = "red",label = 'liner regression',linewidth = 2)
plt.xlabel('data')
plt.ylabel('target')
plt.title('Decision Tree Regression')
plt.legend()#显示图中的标签label
plt.show()
3、集成学习
(1)Bagging:
创建多个小分类器,同时学习,最终的分类器是平均这些单独分类器的输出,在分类算法中这种技术称为投票。
#max_samples随机选取50%的样本训练
model = ensemble.BaggingClassifier(base_estimator=neighbors.KNeighborsClassifier(),
n_estimators=50,max_samples=0.5,max_features=0.5)
(2)随机森林:
随机森林是非常具有代表性的Bagging集成算法,它的所有基评估器都是决策树
model = ensemble.RandomForestClassifier(n_estimators=25,max_depth=3)
(3)Adaboost:
Adaboost算法是一种提升方法,将多个弱分类器组合成强分类器,每个弱分类器都占有权重,分类误差大的弱分类器权重较小。
model = ensemble.AdaBoostClassifier(n_estimators=100)
(4)GBRT:
主要思想:每一次建立模型都是在之前建立模型损失函数的梯度下降方向,每一次都是在上一次残差的基础上计算,减少上一次的残差。
from sklearn import ensemble
import numpy as np
import matplotlib.pyplot as plt
x = np.array(list(range(1,11))).reshape(-1,1)
y = np.array([5.56, 5.70, 5.91, 6.40, 6.80, 7.05, 8.90, 8.70, 9.00, 9.05])
model = ensemble.GradientBoostingRegressor(max_depth=2,n_estimators=20)
model.fit(x,y)
x_test = np.arange(0.0,10.0,0.01)[:,None]
y_1 = model.predict(x_test)
plt.scatter(x,y,s=20,edgecolors='black',c="darkorange", label="data")
plt.plot(x_test,y_1,color = 'red',label = 'max_depth=2',linewidth=2)
plt.xlabel('data')
plt.ylabel('target')
plt.title('Decision Tree Regression')
plt.legend()
plt.show()
五、聚类
1、Kmeans
原理:已知要分为几类,假如分为两类,随机选取两个中心点,每个样本点都与这两个点计算距离,离那个点近,就把样本点归为哪一类,计算完一轮之后重新计算两堆点的平均值,随机选取的中心点被更新为两堆点的平均值,然后再次计算距离更新中心点,不断迭代,直至聚类中心不再发生变化。
2、Kmeans++
对选取初始中心点进行了改进,聚类过程和Kmeans一致。首先从样本点中选取一个聚类中心;然后计算所有样本点与中心的距离,所有非聚类中心样本点被选取作为下一中心点的概率与距离大小有关,距离越大,被选为下一中心点的概率越大;重复计算距离和选取中心点,直至选取的中心点个数与设定分为几类相同时使用Kmeans算法。
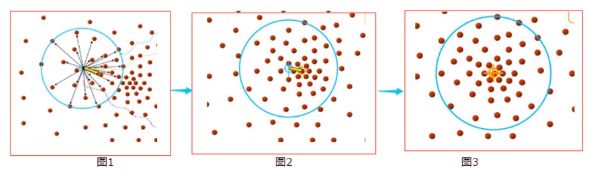
3、MeanShift(均值迁移)
基本思想:在数据集中选取一个点,然后以这个点为圆心,以R为半径画圆(二维是圆),求出这个点与圆内所有点的向量平均值,而圆心与向量平均值的和作为新的圆心,然后迭代此过程直到满足某一条件。
4、层次聚类
层次聚类根据层次分解的顺序可以分为自下向上和自上向下。
自下向上就是一开始所有的样本点都是一个类别,每个类别都与其它类别计算距离,计算距离的方法有:最短距离法、最长距离法、中间距离法、类平均法等,如果按最短距离法进行划分,距离最近的两个点归为一类 ,然后不断计算类与类之间的距离,直至合并成一个类。
自上而下就是反过来,一开始所有的个体都属于一个类,然后根据距离排除异己,最后每个个体都成为一个类。
优点:距离和规则的相似度容易定义,限制少;不需要预先设定聚类数;可以发现类的层次关系;可以聚类成其它形状。
缺点:计算复杂度太高,计算量大;奇异值也能产生很大的影响;算法很可能聚类成链状。
5、密度聚类
邻域:对于任意给定的样本x和距离 ε \varepsilon ε ,x的 ε \varepsilon ε邻域是指到x距离不超过 ε \varepsilon ε的样本的集合;
核心对象:若样本x的 ε \varepsilon ε邻域内至少包含minPts个样本,则x是一个核心对象;
密度直达:若样本b在x的邻域 ε \varepsilon ε内,则a是核心对象,则成样本b由样本x密度直达;
密度可达:对于样本a、b,如果存在p1,p2,…,pn,其中p1=a,p2=b,且序列中每一个样本都与它的前一个样本密度直达,则称样本a与b密度可达;
密度相连:对于样本a和b,若存在样本k使得a与k密度可达,且k与b密度可达,则a与b密度相连。
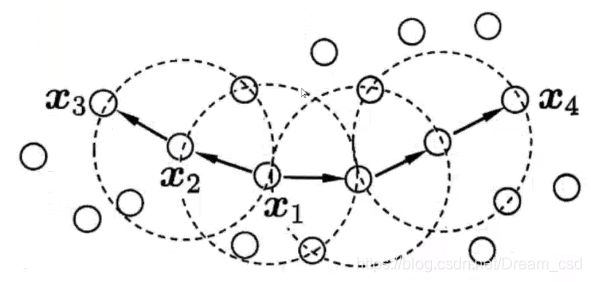
当minPts=3时,虚线圈表示邻域,x1是核心对象;x2
由x1密度直达;x3由x1密度可达;x3与x4密度相连。
6、混合高斯
EM算法:
基本思想:最大期望算法是一种通过迭代进行极大似然估计的优化算法,用于对包含隐变量或缺失数据的概率模型进行参数估计。
第一步:计算期望(M),固定参数θ,求隐变量z的概率分布;
第二部:最大化(E),最大化在E步上求得的概率分布来计算参数θ的值。
M步上找到的参数估计值被用于下一个E步计算中,不断迭代直至参数收敛。
算法流程:
输入:观察数据 x = ( x ( 1 ) , x ( 2 ) , . . . x ( m ) ) x=(x_{(1)},x_{(2)},...x_{(m)}) x=(x(1),x(2),...x(m)),联合分布 p ( x , z ; θ ) p(x,z ;\theta) p(x,z;θ),条件分布 p ( z ∣ x ; θ ) p(z|x; \theta) p(z∣x;θ),最大迭代次数 J J J
1)随机初始化模型参数 θ \theta θ的初值 θ 0 \theta_0 θ0。
2) f o r j f r o m 1 t o j for \ j \ from \ 1 \ to \ j for j from 1 to j:
a) E步。计算联合分布的条件概率期望:
Q i ( z ( i ) ) = P ( z ( i ) ∣ x ( i ) , θ j ) Q_i(z_{(i)}) = P( z_{(i)}|x_{(i)}, \theta_{j}) Qi(z(i))=P(z(i)∣x(i),θj)
L ( θ , θ j ) = ∑ i = 1 m ∑ z ( i ) P ( z ( i ) ∣ x ( i ) , θ j ) l o g P ( x ( i ) , z ( i ) ; θ ) L(\theta, \theta_{j}) = \sum\limits_{i=1}^m\sum\limits_{z_{(i)}}P( z_{(i)}|x_{(i)}, \theta_{j})log{P(x_{(i)}, z_{(i)};\theta)} L(θ,θj)=i=1∑mz(i)∑P(z(i)∣x(i),θj)logP(x(i),z(i);θ)
b) M步。极大化 L ( θ , θ j ) L(\theta, \theta_{j}) L(θ,θj),得到 θ j + 1 \theta_{j+1} θj+1:
θ j + 1 = arg max θ L ( θ , θ j ) \theta_{j+1} = \mathop{\arg\max}_\theta L(\theta, \theta_{j}) θj+1=argmaxθL(θ,θj)
c) 如果 θ j + 1 \theta_{j+1} θj+1收敛,则算法结束。否则继续回到步骤a)进行E步迭代。
输出:模型参数 θ \theta θ。
EM算法是否收敛:
EM算法一定会收敛到一个稳定点,但是不能保证收敛到全局极大值点,因此它是局部最优算法。
EM算法实例:
EM算法是在数据不完全的情况下的参数估计。我们用一个投硬币的例子来解释EM算法流程。假设我们有A,B两枚硬币,其中正面朝上的概率分别为 θ A , θ B \theta_{A},\theta_{B} θA,θB,这两个参数即为需要估计的参数。我们设计5组实验,每次实验投掷5次硬币,但是每次实验都不知道用哪一枚硬币进行的本次实验。投掷结束后,会得到一个数组 x = ( x 1 , x 2 , . . . x 5 ) x=(x_{1},x_{2},...x_{5}) x=(x1,x2,...x5) ,表示每组实验有几次硬币正面朝上,因此 0 ≤ x i ≥ 5 0\leq x_{i} \geq 5 0≤xi≥5。
如果我们知道每一组实验中 x i x_{i} xi 是A硬币投掷的结果还是B硬币投掷的结果,我们可以很容易的估算出 θ A , θ B \theta_{A},\theta_{B} θA,θB ,只需要统计所有的实验中两个硬币分别正面朝上的次数,然后除以它们各自投掷的总次数。但是,数据不完全的意思在于,我们并不知道每一个数据是由哪一枚硬币产生的。EM算法可以解决类似这样的问题。
虽然我们不知道每组实验用的是哪一枚硬币,但如果我们用某种方法猜测每组实验是哪个硬币投掷的,我们就可以将数据缺失的估计问题转化成一个最大似然问题和完整参数估计问题。
假设5次试验的结果如下:
| 硬币 | 结果 | 统计 |
|---|---|---|
| 未知 | 正正反正反 | 3正-2反 |
| 未知 | 反反正正反 | 2正-3反 |
| 未知 | 正反反反反 | 1正-4反 |
| 未知 | 正反反正正 | 3正-2反 |
| 未知 | 反正正反反 | 2正-3反 |
首先,随机选取 θ A , θ B \theta_{A},\theta_{B} θA,θB 的初始值,比如 θ A = 0.2 , θ B = 0.7 \theta_{A}=0.2,\theta_{B}=0.7 θA=0.2,θB=0.7 。EM算法的E步骤,是计算在当前的预估参数下,隐含变量(是A硬币还是B硬币)的每个值出现的概率。也就是给定 θ A , θ B \theta_{A},\theta_{B} θA,θB和观测数据,计算这组数据出自A硬币的概率和这组数据出自B硬币的概率。对于第一组实验,3正面2反面。
如果是A硬币得到这个结果的概率为: 0. 2 2 × 0. 8 2 = 0.00515 0.2^2\times0.8^2=0.00515 0.22×0.82=0.00515
如果是B硬币得到这个结果的概率为: 0. 7 2 × 0. 3 2 = 0.03087 0.7^2\times0.3^2=0.03087 0.72×0.32=0.03087
因此,第一组实验结果是A硬币得到的概率为:0.00512 / (0.00512 + 0.03087)=0.14,第一组实验结果是B硬币得到的概率为:0.03087/ (0.00512 + 0.03087)=0.86。整个5组实验的A,B投掷概率如下:
| 轮数 | A硬币 | B硬币 |
|---|---|---|
| 1 | 0.14 | 0.86 |
| 2 | 0.61 | 0.39 |
| 3 | 0.94 | 0.06 |
| 4 | 0.14 | 0.86 |
| 5 | 0.61 | 0.39 |
根据隐含变量的概率,可以计算出两组训练值的期望。依然以第一组实验来举例子:3正2反中,如果是A硬币投掷的结果:0.143=0.42个正面和0.142=0.28个反面;如果是B硬币投掷的结果:0.863=2.58个正面和0.862=1.72个反面。
5组实验的期望如下表:
| 轮数 | 正面 反面(A硬币) | 正面 反面(B硬币) |
|---|---|---|
| 1 | 0.42 0.28 | 2.58 1.72 |
| 2 | 1.22 1.83 | 0.78 1.17 |
| 3 | 0.64 3.76 | 0.06 0.24 |
| 4 | 0.42 0.28 | 2.58 1.72 |
| 5 | 1.22 1.83 | 0.78 1.17 |
| 总计 | 4.22 7.89 | 6.78 6.02 |
通过计算期望,我们把一个有隐含变量的问题变化成了一个没有隐含变量的问题,由上表的数据,估计 θ A , θ B \theta_{A},\theta_{B} θA,θB变得非常简单。
θ A \theta_{A} θA =4.22/(4.22+7.98)=0.35
θ B \theta_{B} θB =6.78/(6.78+6.02)=0.5296875
这一步中,我们根据E步中求出的A硬币、B硬币概率分布,依据最大似然概率法则去估计 θ A , θ B \theta_{A},\theta_{B} θA,θB,被称作M步。
最后,一直循环迭代E步M步,直到 θ A , θ B \theta_{A},\theta_{B} θA,θB不更新为止。
7、聚类衡量指标
轮廓系数:
取值范围[-1,1],值越大表示分类效果越好,对于非凸集评价效果不好
CH分数:
取值范围大于0,值越大越好,同样对于非凸集评价效果不好
戴维森堡丁指数(DBI):
值越小越好,越小意味着类内间距越小,类间间距越大。缺点:因使用欧氏距离所以对于环状分布聚类评测很差。
8、聚类代码实现
import matplotlib.pyplot as plt
from sklearn.mixture import GaussianMixture
from sklearn.datasets import samples_generator
from sklearn import metrics, cluster
# X, _ = samples_generator.make_blobs(n_samples=200, centers=2, cluster_std=0.60, random_state=0)
X, y_true = samples_generator.make_moons(200, noise=.05, random_state=0)
# X, y_true = samples_generator.make_circles(200, noise=0.05, random_state=0,factor=0.4)
# gmm = GaussianMixture(n_components=2)#混合高斯
# gmm = cluster.MeanShift()
# gmm = cluster.KMeans(4)
# gmm = cluster.AgglomerativeClustering(2)#层次聚类
# gmm = cluster.AffinityPropagation()#吸引子传播算法
gmm = cluster.SpectralClustering(2,affinity="nearest_neighbors")#谱聚类
# gmm = cluster.DBSCAN()#密度聚类
labels = gmm.fit_predict(X)
print(metrics.silhouette_score(X, labels))
print(metrics.calinski_harabasz_score(X, labels))
print(metrics.davies_bouldin_score(X, labels))
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis');
plt.show()
六、降维
1、主成分分析(PCA)
(1)核心思想:
(1)PCA可以解决训练数据中存在数据特征过多或特征累赘的问题,就是将高维的数据通过线性变换投影到低维空间
(2)投影思想:找出能够代表原始数据的投影方法,被PCA降掉的那些数据只能是噪音和冗余的数据
(3)去冗余:去除可以被其它向量代表的线性相关向量,这些信息是多余的
(4)去噪音:去除特征值较小的特征向量,特征值越大表示变换后在特征向量的方向上的元素差异较大,该特征越重要,需要保留
(5)完成PCA的关键就是找到协方差矩阵,cov矩阵能够同时表现不同维度间的相关性以及各个维度上的方差,得到cov矩阵后进行相似对角化,寻找极大线性无关组,保留较大的特征值,去除较小的特征值,组成一个投影矩阵,对原始样本进行投影,得到降维后的新样本
(2)算法优缺点:
| 优缺点 | 简要说明 |
|---|---|
| 优点 | 1. 仅仅需要以方差衡量信息量,不受数据集以外的因素影响。 2.各主成分之间正交,可消除原始数据成分间的相互影响的因素。3. 计算方法简单,主要运算是特征值分解,易于实现。 |
| 缺点 | 1.主成分各个特征维度的含义具有一定的模糊性,不如原始样本特征的解释性强。2. 方差小的非主成分也可能含有对样本差异的重要信息,因降维丢弃可能对后续数据处理有影响。 |
(3)代码实现:
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
# 载入样本
iris = load_iris()
X, y = iris.data, iris.target
# 降维、设置参数
pca3 = PCA(n_components=3) # 降到3d
X3 = pca3.fit_transform(X)
print(pca3.explained_variance_ratio_)
pca2 = PCA(n_components=2) # 降到2d
X2 = pca2.fit_transform(X)
print(pca2.explained_variance_ratio_)
# 绘图
ax = mplot3d.Axes3D(plt.figure(figsize=(4, 3)))
ax.scatter(X3[:, 0], X3[:, 1], X3[:, 2], s=88, c=y, alpha=0.5)
plt.show()
plt.scatter(X2[:, 0], X2[:, 1], s=88, c=y, alpha=0.5)
plt.show()
2、线性判别分析(LDA)
(1)核心思想:
线性判别分析(Linear Discriminant Analysis,LDA)是一种经典的降维方法。和主成分分析PCA不考虑样本类别输出的无监督降维技术不同,LDA是一种监督学习的降维技术,数据集的每个样本有类别输出。
LDA分类思想简单总结如下:
- 多维空间中,数据处理分类问题较为复杂,LDA算法将多维空间中的数据投影到一条直线上,将d维数据转化成1维数据进行处理。
- 对于训练数据,设法将多维数据投影到一条直线上,同类数据的投影点尽可能接近,异类数据点尽可能远离。
- 对数据进行分类时,将其投影到同样的这条直线上,再根据投影点的位置来确定样本的类别。
如果用一句话概括LDA思想,即“投影后类内方差最小,类间方差最大”。
(2)LDA和PCA区别:
| 异同点 | LDA | PCA |
|---|---|---|
| 相同点 | 1. 两者均可以对数据进行降维; 2. 两者在降维时均使用了矩阵特征分解的思想; 3. 两者都假设数据符合高斯分布; |
|
| 不同点 | 有监督的降维方法; | 无监督的降维方法; |
| 降维最多降到k-1维; | 降维多少没有限制; | |
| 可以用于降维,还可以用于分类; | 只用于降维; | |
| 选择分类性能最好的投影方向; | 选择样本点投影具有最大方差的方向; | |
| 更明确,更能反映样本间差异; | 目的较为模糊; |
(3)优缺点:
| 优缺点 | 简要说明 |
|---|---|
| 优点 | 1. 可以使用类别的先验知识; 2. 以标签、类别衡量差异性的有监督降维方式,相对于PCA的模糊性,其目的更明确,更能反映样本间的差异; |
| 缺点 | 1. LDA不适合对非高斯分布样本进行降维; 2. LDA降维最多降到分类数k-1维; 3. LDA在样本分类信息依赖方差而不是均值时,降维效果不好; 4. LDA可能过度拟合数据。 |
(4)代码实现:
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
# 载入样本
iris = load_iris()
X, y = iris.data, iris.target
# 降维、设置参数
lda3 = LinearDiscriminantAnalysis(n_components=3)
lda3.fit(X, y)
X3 = lda3.transform(X)
print(lda3.explained_variance_ratio_)
# 绘图
plt.scatter(X3[:, 0], X3[:, 1], s=88, c=y, alpha=0.5)
plt.show()