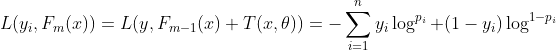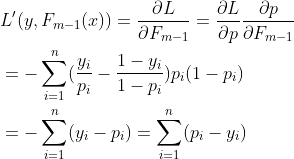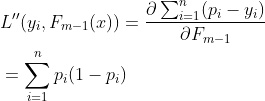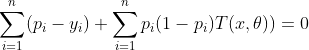GBDT-梯度提升决策树
前面介绍了决策树和集成算法的相关知识,本章介绍的GBDT(Gradient Boosting Decision Tree)是这两个知识点的融合,GBDT所采用的树模型是CART回归树,将回归树改造后,GBDT不仅用于回归也可用于分类,GBDT与SVM支持向量机被认为是泛化能力较强的模型。名称中的提升(Boosting)说明该算法是一种集成算法,与AdaBoosting不同的是:GBDT集成的对象必须是CART树,而AdaBoosting集成目标是弱分类器;两者迭代的方式也有区别,AdaBoosting利用上一轮错误率来更新下一轮分类器的权重、从而实现最终识别能力的提升,而GBDT使用梯度来实现模型的提升,算法中利用残差来拟合梯度,通过不断减小残差实现梯度的下降。
一、GBDT实现回归
1.1 残差的概念
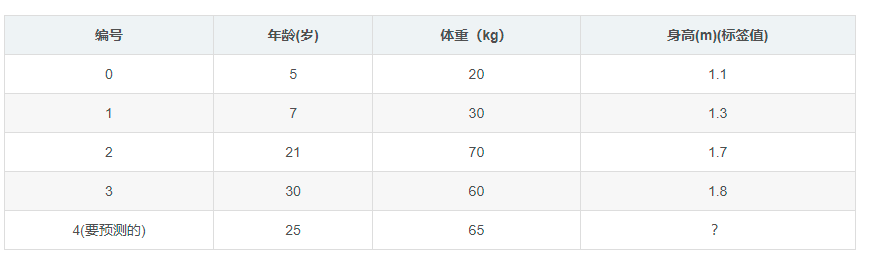
首先来了解残差概念,假设有一组数据分别是:5、6、7,取平均数6为每个数据的预测值,则三个数据残差分别为5-6、6-6、7-6:-1,0,1,残差可以定义为真实值与预测值之间的差值。GBDT实现回归功能时,通常取平均值作为初始值或称之为第0轮预测值,利用0轮预测值可得到每个数据的残差,将残差作为目标值训练CART决策树,根据设置CART树层数阈值、分裂数目等规则,新生成CART树叶节点中可能为一个含有初始残差的集合,也有可能只有一个残差元素;得到CART树后将得到一组新的残差值,将新的一组残差值输入下一轮再生成CART树,依次类推,最后残差值会越来越小,代表着GBDT模型逐步拟合真实的数据从而实现回归。下面通过一个示例来说明GBDT实现回归的过程,样本有年龄、体重两个属性,需要通过这两个属性预测目标值身高:
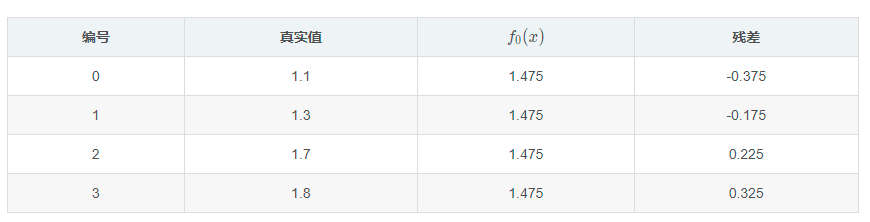
初始时取身高平均值1.475作为预测值,并得到初始残差数据:
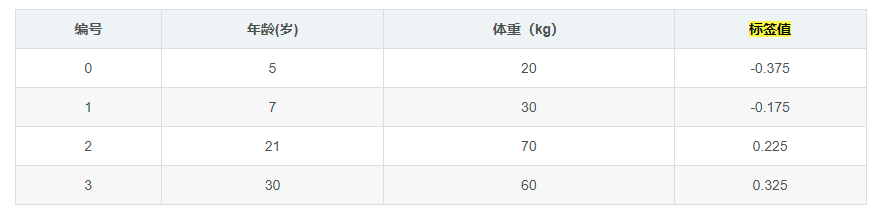
将残差作为目标数据训练CART回归树:
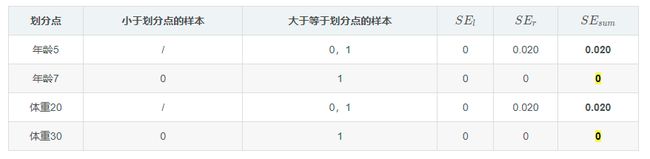
CART树实现回归原理在CART树分类、回归、剪枝实现一章中已经介绍过,假设以年龄小于7岁作为分裂点,小于7岁数据只有年龄为5岁的样本,其平方误差为(-0.375-(-0.375))^2=0,将其定义为左结点误差SEl,即SEl=0;而大于等于7岁的样本残差平均值为(-0.175+0.225+ 0.325)/3 =0.125,可得到右结点误差SEr:
SEr=(-0.175-0.125)^2+(0.225-0.125)^2+( 0.325-0.125)^2=0.140
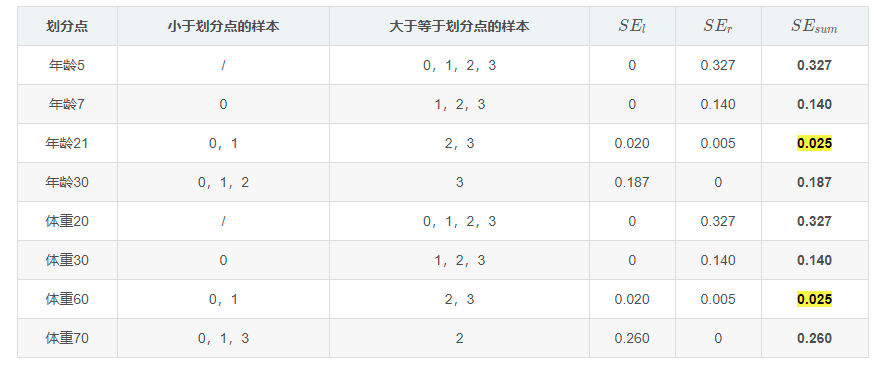
依次计算,取SEr+SEl值最小的点作为属性分裂结点,得到下面的表:
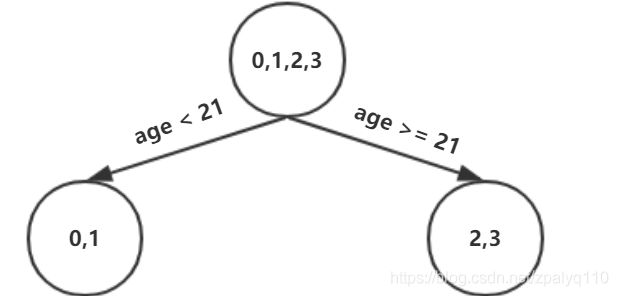
可以看出选择年龄为21或体重为60作为属性分裂点,其平方误差最小,不妨选择年龄为21作为分裂点,这样就得到第一棵CART树:
可以看出这颗CART树叶结点含有多个残差元素,以左结点为例含有编号为0,1两个数据,如果不继续分裂,那么通常取残差的平均值作为该叶结点的'得分':
scoreleft=(-0.375-0.175)/2=-0.275
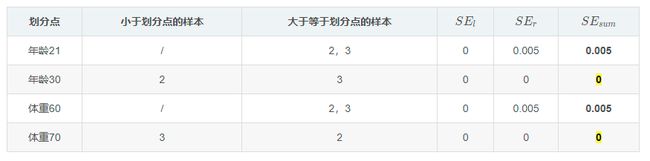
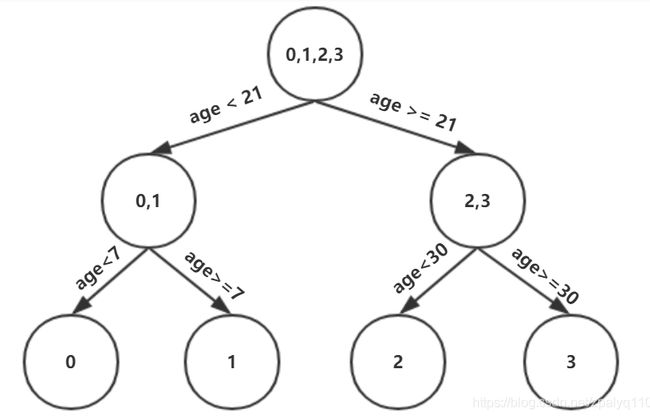
这时编号0的新的残差为:1.1-(1.475-0.275)=-0.100,式中的1.475-0.275是截止到目前的预测值,可以看出:-0.100比起先前的残差-0.375误差缩小了很多(比较绝对值),同样编号为1数据残差为0.1,比起初始残差-0.175误差也缩小了。这颗CART树深度是2,如果设置CART树的深度为3,那么可以对上面的树继续展开,以左结点0,1为例,继续计算各个属性区间的平方误差可得到下表:
同样得到右结点平方误差表:
选择平方误差最小属性值作为分裂结点,可得到三层结构的CART树:
利用CART树得到一组新的残差,接下来将新的残差值作为目标值训练第二棵CART树,具体要迭代到第几棵树终止计算,可以通过设置树的数量,而最终的预测值是把初始预测值与所有树叶节点的残差相加。需要强调的是,当CART树叶结点包含多个元素时,需要对叶节点打分,就回归问题而言,取平均值就可以了,GBDT实现分类甚至跟高阶的xgboost模型都有打分这个环节,根据问题的不同打分的方式也有区别。
1.2 公式推导
上面的例子中利用了残差,到目前为止并未出现梯度的概念,之前说过了,GBDT利用残差来代替梯度,接下来通过推导来了解回归问题中残差、梯度、CART树三者的关系,GBDT回归函数可用下面的公式表示:
![]() ⑴
⑴
公式中m代表迭代轮数,m>=1,![]() 代表前m-1轮回归函数,而
代表前m-1轮回归函数,而![]() 代表m轮需要求解的CART回归树,特殊的,当m=1时,就回归问题而言,F0(x)是目标值的平均数,在代码实现中称之为初始值。
代表m轮需要求解的CART回归树,特殊的,当m=1时,就回归问题而言,F0(x)是目标值的平均数,在代码实现中称之为初始值。![]() 、
、![]() 、
、![]() 其实都是分段函数,一个编号为i的样本数据,①式可写成:
其实都是分段函数,一个编号为i的样本数据,①式可写成:
![]() (1.1)
(1.1)
解决回归问题常用平方差函数作为损失函数,假设已经得到m-1轮回归函数![]() ,则有损失函数:
,则有损失函数:
将![]() 视为一个变量,对
视为一个变量,对![]() 求导可得(1.2)的梯度:
求导可得(1.2)的梯度:
上式中![]() 即为之前介绍的残差,m-1轮、第i个数据的残差可用
即为之前介绍的残差,m-1轮、第i个数据的残差可用![]() 表示,另外要使得(1.2)式损失函数值变小,需要沿当前
表示,另外要使得(1.2)式损失函数值变小,需要沿当前![]() 梯度的负方向前进,这样就可以得到
梯度的负方向前进,这样就可以得到![]() 的表达式:
的表达式:
上式中λ称为步长系数,在代码实现中也称为学习率,(1.4)进一步可写成:
![]() (1.5)
(1.5)
由(1.1)和(1.5)式可知,每轮求解的CART树![]() 与损失函数梯度、残差,三者间有着对应关系:
与损失函数梯度、残差,三者间有着对应关系:
当损失函数(1.2)的梯度为0时即到达了极值点,也就是损失函数获得了最小值,梯度等于0时残差也必然接近0,在GBDT算法中没有梯度的计算,原因是梯度与残差是协同、等效的,通过降低残差可以实现降低梯度,而残差的降低又是通过CART树实现的,所以说,迭代生成CART树的过程本质是梯度减小的过程,是一个二次函数优化的过程。
1.3 GBDT的python实现
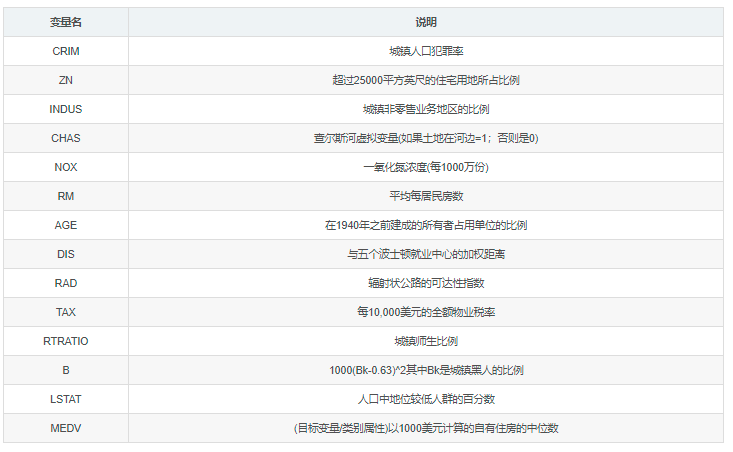
接下来用sklearn自带的GBDT算法GradientBoostingRegressor分析波士顿房价数据集,该数据集有十几个属性,目标值是房价,属性定义分别为:
实现代码如下:
from sklearn import datasets
import numpy as np
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.utils import shuffle
from sklearn.metrics import mean_squared_error
def loaddata(splitset=0.9):
boston = datasets.load_boston()
X, y = shuffle(boston.data, boston.target, random_state=13)
X = X.astype(np.float32)
offset = int(X.shape[0] * splitset)
X_train, y_train = X[:offset], y[:offset]
X_test, y_test = X[offset:], y[offset:]
return X_train,y_train,X_test,y_test
def sklearnGBDT():
X_train, y_train, X_test, y_test=loaddata()
gbdt = GradientBoostingRegressor(
loss='ls'
, learning_rate=0.01
, n_estimators=500
, subsample=1
, min_samples_split=2
, min_samples_leaf=1
, max_depth=10
, init=None
, random_state=None
, max_features='log2'
, alpha=0.9
, verbose=0
, max_leaf_nodes=None
, warm_start=False
)
gbdt.fit(X_train, y_train)
pred = gbdt.predict(X_test)
total_err = 0
for i in range(pred.shape[0]):
y = y_test[i]
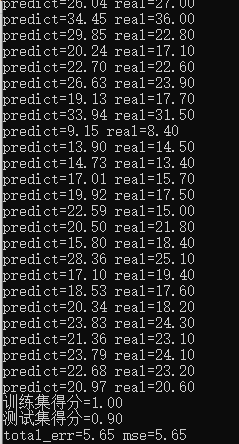
print('predict=%0.2f real=%0.2f' % (pred[i], y))
total_err+=(pred[i]-y)**2
score1 = gbdt.score(X_train, y_train)
score2 = gbdt.score(X_test, y_test)
print('训练集得分=%0.2f' % (score1))
print('测试集得分=%0.2f' % (score2))
mse = mean_squared_error(y_test, pred )
print('total_err=%0.2f mse=%0.2f' % (total_err/pred.shape[0],mse))
if __name__ == "__main__":
sklearnGBDT()
得到模型结果如下:
GradientBoostingRegressor构造函数中有几个参数说明一下:
learning_rate:为学习率,对应公式(1.6)中的参数λ,在优化算法中也成为步长系数。
n_estimators:代表一共需要迭代生成CART树的数量,数量越多拟合能力越强,但训练的时间也会相应的增加。
min_samples_split:是结点分裂阈值,当大于min_samples_split时CART树继续分裂结点,本例中min_samples_split=2说明最后CART树叶结点中都只有一个元素。
max_depth:是每棵树的深度,当深度小于max_depth时继续分裂结点。
max_features:主要是当属性较多时,训练耗时较长,max_features含义是如何选择部分属性生成决策树。
根据上述推导,下面是一个实现的GBDT的python代码,利用的仍然是波士顿房价数据集。
=regression_tree.py= CART回归树代码:
# -*- coding: utf-8 -*-
from copy import copy
import numpy as np
from numpy import ndarray
class Node:
"""Node class to build tree leaves.
Attributes:
avg {float} -- prediction of label. (default: {None})
left {Node} -- Left child node.
right {Node} -- Right child node.
feature {int} -- Column index.
split {int} -- Split point.
mse {float} -- Mean square error.
"""
attr_names = ("avg", "left", "right", "feature", "split", "mse")
def __init__(self, avg=None, left=None, right=None, feature=None, split=None, mse=None):
self.avg = avg
self.left = left
self.right = right
self.feature = feature
self.split = split
self.mse = mse
def __str__(self):
ret = []
for attr_name in self.attr_names:
attr = getattr(self, attr_name)
# Describe the attribute of Node.
if attr is None:
continue
if isinstance(attr, Node):
des = "%s: Node object." % attr_name
else:
des = "%s: %s" % (attr_name, attr)
ret.append(des)
return "\n".join(ret) + "\n"
def copy(self, node):
"""Copy the attributes of another Node.
Arguments:
node {Node}
"""
for attr_name in self.attr_names:
attr = getattr(node, attr_name)
setattr(self, attr_name, attr)
class RegressionTree:
"""RegressionTree class.
Attributes:
root {Node} -- Root node of RegressionTree.
depth {int} -- Depth of RegressionTree.
_rules {list} -- Rules of all the tree nodes.
"""
def __init__(self):
self.root = Node()
self.depth = 1
self._rules = None
def __str__(self):
ret = []
for i, rule in enumerate(self._rules):
literals, avg = rule
ret.append("Rule %d: " % i + ' | '.join(
literals) + ' => y_hat %.4f' % avg)
return "\n".join(ret)
@staticmethod
def _expr2literal(expr: list) -> str:
"""Auxiliary function of get_rules.
Arguments:
expr {list} -- 1D list like [Feature, op, split].
Returns:
str
"""
feature, operation, split = expr
operation = ">=" if operation == 1 else "<"
return "Feature%d %s %.4f" % (feature, operation, split)
def get_rules(self):
"""Get the rules of all the tree nodes.
Expr: 1D list like [Feature, op, split].
Rule: 2D list like [[Feature, op, split], label].
Op: -1 means less than, 1 means equal or more than.
"""
# Breadth-First Search.
que = [[self.root, []]]
self._rules = []
while que:
node, exprs = que.pop(0)
# Generate a rule when the current node is leaf node.
if not(node.left or node.right):
# Convert expression to text.
literals = list(map(self._expr2literal, exprs))
self._rules.append([literals, node.avg])
# Expand when the current node has left child.
if node.left:
rule_left = copy(exprs)
rule_left.append([node.feature, -1, node.split])
que.append([node.left, rule_left])
# Expand when the current node has right child.
if node.right:
rule_right = copy(exprs)
rule_right.append([node.feature, 1, node.split])
que.append([node.right, rule_right])
@staticmethod
def _get_split_mse(col: ndarray, label: ndarray, split: float) -> Node:
"""Calculate the mse of label when col is splitted into two pieces.
MSE as Loss fuction:
y_hat = Sum(y_i) / n, i <- [1, n]
Loss(y_hat, y) = Sum((y_hat - y_i) ^ 2), i <- [1, n]
--------------------------------------------------------------------
Arguments:
col {ndarray} -- A feature of training data.
label {ndarray} -- Target values.
split {float} -- Split point of column.
Returns:
Node -- MSE of label and average of splitted x
"""
# Split label.
label_left = label[col < split]
label_right = label[col >= split]
# Calculate the means of label.
avg_left = label_left.mean()
avg_right = label_right.mean()
# Calculate the mse of label.
mse = (((label_left - avg_left) ** 2).sum() +
((label_right - avg_right) ** 2).sum()) / len(label)
# Create nodes to store result.
node = Node(split=split, mse=mse)
node.left = Node(avg_left)
node.right = Node(avg_right)
return node
def _choose_split(self, col: ndarray, label: ndarray) -> Node:
"""Iterate each xi and split x, y into two pieces,
and the best split point is the xi when we get minimum mse.
Arguments:
col {ndarray} -- A feature of training data.
label {ndarray} -- Target values.
Returns:
Node -- The best choice of mse, split point and average.
"""
# Feature cannot be splitted if there's only one unique element.
node = Node()
unique = set(col)
if len(unique) == 1:
return node
# In case of empty split.
unique.remove(min(unique))
# Get split point which has min mse.
ite = map(lambda x: self._get_split_mse(col, label, x), unique)
node = min(ite, key=lambda x: x.mse)
return node
def _choose_feature(self, data: ndarray, label: ndarray) -> Node:
"""Choose the feature which has minimum mse.
Arguments:
data {ndarray} -- Training data.
label {ndarray} -- Target values.
Returns:
Node -- feature number, split point, average.
"""
# Compare the mse of each feature and choose best one.
_ite = map(lambda x: (self._choose_split(data[:, x], label), x),
range(data.shape[1]))
ite = filter(lambda x: x[0].split is not None, _ite)
# Return None if no feature can be splitted.
node, feature = min(
ite, key=lambda x: x[0].mse, default=(Node(), None))
node.feature = feature
return node
def fit(self, data: ndarray, label: ndarray, max_depth=5, min_samples_split=2):
"""Build a regression decision tree.
Note:
At least there's one column in data has more than 2 unique elements,
and label cannot be all the same value.
Arguments:
data {ndarray} -- Training data.
label {ndarray} -- Target values.
Keyword Arguments:
max_depth {int} -- The maximum depth of the tree. (default: {5})
min_samples_split {int} -- The minimum number of samples required
to split an internal node. (default: {2})
"""
# Initialize with depth, node, indexes.
self.root.avg = label.mean()
que = [(self.depth + 1, self.root, data, label)]
# Breadth-First Search.
while que:
depth, node, _data, _label = que.pop(0)
# Terminate loop if tree depth is more than max_depth.
if depth > max_depth:
depth -= 1
break
# Stop split when number of node samples is less than
# min_samples_split or Node is 100% pure.
if len(_label) < min_samples_split or all(_label == label[0]):
continue
# Stop split if no feature has more than 2 unique elements.
_node = self._choose_feature(_data, _label)
if _node.split is None:
continue
# Copy the attributes of _node to node.
node.copy(_node)
# Put children of current node in que.
idx_left = (_data[:, node.feature] < node.split)
idx_right = (_data[:, node.feature] >= node.split)
que.append(
(depth + 1, node.left, _data[idx_left], _label[idx_left]))
que.append(
(depth + 1, node.right, _data[idx_right], _label[idx_right]))
# Update tree depth and rules.
self.depth = depth
self.get_rules()
def predict_one(self, row: ndarray) -> float:
"""Auxiliary function of predict.
Arguments:
row {ndarray} -- A sample of testing data.
Returns:
float -- Prediction of label.
"""
node = self.root
while node.left and node.right:
if row[node.feature] < node.split:
node = node.left
else:
node = node.right
return node.avg
def predict(self, data: ndarray) -> ndarray:
"""Get the prediction of label.
Arguments:
data {ndarray} -- Testing data.
Returns:
ndarray -- Prediction of label.
"""
return np.apply_along_axis(self.predict_one, 1, data)
=gbdt_base.py=gbdt基类:
# -*- coding: utf-8 -*-
from typing import Dict, List
import numpy as np
from numpy import ndarray
from numpy.random import choice
from regression_tree import Node, RegressionTree
class GradientBoostingBase:
"""GBDT base class.
http://statweb.stanford.edu/~jhf/ftp/stobst.pdf
Attributes:
trees {list}: A list of RegressionTree objects.
lr {float}: Learning rate.
init_val {float}: Initial value to predict.
"""
def __init__(self):
self.trees = None
self.learning_rate = None
self.init_val = None
def _get_init_val(self, label: ndarray):
"""Calculate the initial prediction of y.
Arguments:
label {ndarray} -- Target values.
Raises:
NotImplementedError
"""
raise NotImplementedError
@staticmethod
def _match_node(row: ndarray, tree: RegressionTree) -> Node:
"""Find the leaf node that the sample belongs to.
Arguments:
row {ndarray} -- Sample of training data.
tree {RegressionTree}
Returns:
Node
"""
node = tree.root
while node.left and node.right:
if row[node.feature] < node.split:
node = node.left
else:
node = node.right
return node
@staticmethod
def _get_leaves(tree: RegressionTree) -> List[Node]:
"""Gets all leaf nodes of a regression tree.
Arguments:
tree {RegressionTree}
Returns:
List[Node] -- A list of RegressionTree objects.
"""
nodes = []
que = [tree.root]
while que:
node = que.pop(0)
if node.left is None or node.right is None:
nodes.append(node)
continue
que.append(node.left)
que.append(node.right)
return nodes
def _divide_regions(self, tree: RegressionTree, nodes: List[Node],
data: ndarray) -> Dict[Node, List[int]]:
"""Divide indexes of the samples into corresponding leaf nodes
of the regression tree.
Arguments:
tree {RegressionTree}
nodes {List[Node]} -- A list of Node objects.
data {ndarray} -- Training data.
Returns:
Dict[Node, List[int]]-- e.g. {node1: [1, 3, 5], node2: [2, 4, 6]...}
"""
regions = {node: [] for node in nodes} # type: Dict[Node, List[int]]
for i, row in enumerate(data):
node = self._match_node(row, tree)
regions[node].append(i)
return regions
@staticmethod
def _get_residuals(label: ndarray, prediction: ndarray) -> ndarray:
"""Update residuals for each iteration.
Arguments:
label {ndarray} -- Target values.
prediction {ndarray} -- Prediction of label.
Returns:
ndarray -- residuals
"""
return label - prediction
def _update_score(self, tree: RegressionTree, data: ndarray, prediction: ndarray,
residuals: ndarray):
"""update the score of regression tree leaf node.
Arguments:
tree {RegressionTree}
data {ndarray} -- Training data.
prediction {ndarray} -- Prediction of label.
residuals {ndarray}
Raises:
NotImplementedError
"""
raise NotImplementedError
def fit(self, data: ndarray, label: ndarray, n_estimators: int, learning_rate: float,
max_depth: int, min_samples_split: int, subsample=None):
"""Build a gradient boost decision tree.
Arguments:
data {ndarray} -- Training data.
label {ndarray} -- Target values.
n_estimators {int} -- number of trees.
learning_rate {float} -- Learning rate.
max_depth {int} -- The maximum depth of the tree.
min_samples_split {int} -- The minimum number of samples required
to split an internal node.
Keyword Arguments:
subsample {float} -- Subsample rate without replacement.
(default: {None})
"""
# Calculate the initial prediction of y.
self.init_val = self._get_init_val(label)
# Initialize prediction.
n_rows = len(label)
prediction = np.full(label.shape, self.init_val)
# Initialize the residuals.
residuals = self._get_residuals(label, prediction)
# Train Regression Trees
self.trees = []
self.learning_rate = learning_rate
idx = range(n_rows)
data_sub = data[idx]
for _ in range(n_estimators):
residuals_sub = residuals[idx]
prediction_sub = prediction[idx]
# Train a Regression Tree by sub-sample of X, residuals
tree = RegressionTree()
tree.fit(data_sub, residuals_sub, max_depth, min_samples_split)
# Update scores of tree leaf nodes
#self._update_score(tree, data_sub, prediction_sub, residuals_sub)
# Update prediction
prediction = prediction + learning_rate * tree.predict(data)
# Update residuals
residuals = self._get_residuals(label, prediction)
self.trees.append(tree)
def predict_one(self, row: ndarray) -> float:
"""Auxiliary function of predict.
Arguments:
row {ndarray} -- A sample of training data.
Returns:
float -- Prediction of label.
"""
# Sum prediction with residuals of each tree.
residual = np.sum([self.learning_rate * tree.predict_one(row)
for tree in self.trees])
return self.init_val + residual
pass
=gbdt_regressor.py= gbdt实现代码:
# -*- coding: utf-8 -*-
import numpy as np
from numpy import ndarray
from gbdt_base import GradientBoostingBase
class EXGradientBoostingRegressor(GradientBoostingBase):
"""Gradient Boosting Regressor"""
def _get_init_val(self, label: ndarray):
"""Calculate the initial prediction of y
Set MSE as loss function, yi <- y, and c is a constant:
L = MSE(y, c) = Sum((yi-c) ^ 2) / n
Get derivative of c:
dL / dc = Sum(-2 * (yi-c)) / n
dL / dc = -2 * (Sum(yi) / n - Sum(c) / n)
dL / dc = -2 * (Mean(yi) - c)
Let derivative equals to zero, then we get initial constant value
to minimize MSE:
-2 * (Mean(yi) - c) = 0
c = Mean(yi)
----------------------------------------------------------------------------------------
Arguments:
label {ndarray} -- Target values.
Returns:
float
"""
return label.mean()
def _update_score(self, tree, data: ndarray, prediction: ndarray, residuals: ndarray):
"""update the score of regression tree leaf node
Fm(xi) = Fm-1(xi) + fm(xi)
Loss Function:
Loss(yi, Fm(xi)) = Sum((yi - Fm(xi)) ^ 2) / n
Taylor 1st:
f(x + x_delta) = f(x) + f'(x) * x_delta
f(x) = g'(x)
g'(x + x_delta) = g'(x) + g"(x) * x_delta
1st derivative:
Loss'(yi, Fm(xi)) = -2 * Sum(yi - Fm(xi)) / n
2nd derivative:
Loss"(yi, Fm(xi)) = 2
So,
Loss'(yi, Fm(xi)) = Loss'(yi, Fm-1(xi) + fm(xi))
= Loss'(yi, Fm-1(xi)) + Loss"(yi, Fm-1(xi)) * fm(xi) = 0
fm(xi) = - Loss'(yi, Fm-1(xi)) / Loss"(yi, Fm-1(xi))
fm(xi) = 2 * Sum(yi - Fm-1(xi) / n / 2
fm(xi) = Sum(yi - Fm-1(xi)) / n
fm(xi) = Mean(yi - Fm-1(xi))
----------------------------------------------------------------------------------------
Arguments:
tree {RegressionTree}
data {ndarray} -- Training data.
prediction {ndarray} -- Prediction of label.
residuals {ndarray}
"""
pass
def predict(self, data: ndarray) -> ndarray:
"""Get the prediction of label.
Arguments:
data {ndarray} -- Training data.
Returns:
ndarray -- Prediction of label.
"""
return np.apply_along_axis(self.predict_one, axis=1, arr=data)
=run.py= 测试代码:
from sklearn import datasets
import numpy as np
from sklearn.utils import shuffle
from gbdt_regressor import EXGradientBoostingRegressor
def loaddata(splitset=0.9):
boston = datasets.load_boston()
X, y = shuffle(boston.data, boston.target, random_state=13)
X = X.astype(np.float32)
offset = int(X.shape[0] * splitset)
X_train, y_train = X[:offset], y[:offset]
X_test, y_test = X[offset:], y[offset:]
return X_train,y_train,X_test,y_test
def mygbdt():
X_train, y_train, X_test, y_test = loaddata()
gbdt=EXGradientBoostingRegressor()
gbdt.fit(data=X_train, label=y_train, n_estimators=500,
learning_rate=0.01, max_depth=5, min_samples_split=2 )
y_ = gbdt.predict(X_test)
total_err = 0
for i in range(y_.shape[0]):
print('predict=%0.2f real=%0.2f'%(y_[i],y_test[i]))
total_err += (y_[i] - y_test[i]) ** 2
print('total_err=%0.2f ' % (total_err / y_test.shape[0] ))
if __name__ == "__main__":
mygbdt()
print('-'*100)
二、GBDT实现分类
2.1 GBDT实现二分类原理
从GBDT实现回归可以看出,CART树的叶子节点值(得分)是一个实数,GBDT实现回归时,得分值取平均值即可,而分类问题常用交叉熵作为损失函数,这就需要把实数变换为概率,逻辑回归一章中曾介绍过,利用Sigmod函数可把实数变为概率形式:
Sigmod函数的导数为:
![]()
与实现回归时一样,设第m轮CART分类树![]() :
:
![]()
编号i的数据概率为:
对于二分类问题,编号i的实际概率yi等于0或1,设有n个数据,以交叉熵作为损失函数有:
对于一个有二阶导数函数,可先展开为一阶泰勒级数形式:
![]()
两边求导的得:
![]()
将(2.1)式中的Fm-1(x)看成上式中的x,T(x,θ)看成上式中的△x,则损失函数一阶导数可表示为:
接下来通过求导法则求出![]() :
:
与回归问题一样,(2.2.1)中出现分类问题的残差:yi-pi,残差与一阶导数即梯度也存在着协同、对应的关系,接下来求二阶导数:
当(2.2)式等于0时,损失函数取得最小值,将(2.2.1)和(2.2.2)带入(2.2)有:
这样就得到CART分类树的表达形式,在代码实现中用下面的公式对叶节点打分:
(2.3)式的分子可以写成残差形式:
通过以上推导再来梳理一下GBDT分类算法中残差、梯度、决策树三者之间的关系,由(2.2.1)式可以看出残差与梯度是等效的,降低残差即可实现降低梯度,反之亦然;而通过求导损失函数并取0时得到的分类树的函数形式,当每轮的CART树满足该形式时可有效的降低梯度以及残差,GBDT实现分类或回归都是利用三者之间的等效协同性,归纳一下:GBDT本质与其他优化问题一样,依然是降低梯度,而梯度的表现形式是残差,通过迭代CART树不断缩小残差范围,间接的降低梯度直至到极值点。
利用公式(2.2.1)可以得到分类树的初始值:F0(x),回归问题中初始值取目标值的平均数作为初始值,在分类算法中,目标值是0或1且使用交叉熵函数作为损失函数,这里需要稍微处理下:与回归问题一样,分类时初始值希望用一个值来作为预测值,不妨设用一个待求参数概率p表示,p带入(2.2.1)有:
余下文章请转至链接: GBDT详解