异常检测：从异常检测到PCA再到特征向量

20201001 -

0. 引言

最近的精力比较杂，当时仅仅是想学习《异常点检测》中的某个章节，但是因为遗忘的知识太多，导致又得学习更多的东西，比如线性代数的东西。很多概念在本科的时候都学过，所以捡起来也不是那么难，但是想马上得心应手的用起来，肯定是要花点功夫的。

在最近看的几个主体中，我就发现了一个非常重要的概念，那就是特征向量。其实这个东西，本身没什么难点嘛，大一学习的线性代数，不就是几个公式，然后求一求就出来了。当时的应试场景下，这样肯定是没什么问题的，但是当真正需要利用这个东西的实际意义的时候，而不是说仅仅是利用这个东西作为一个方程的解的时候，那就需要对这部分内容有深入的理解才行。

所以，本部分内容就将记录我这几天看这些东西学到的东西，从基础的异常点检测，再到特征向量，当然我现在也不能说就非常理解了，但是基本上已经算是明白怎么回事了，后续就是需要利用这部分东西慢慢的消化。

一开始想着这篇文章就从基础开始讲起，然后最后再到主题，但是仔细想了想，还是不要这样了，因为我本身产生这些内容的过程就是在学习某个主题，然后才延伸到了基础的内容，所以这里我也打算使用这样的方法。

这是这个系列的第一篇文章，第二篇文章是《线性代数 - 矩阵形式下的最小二乘法》。

1. 异常检测

本篇文章的内容都是在阅读书《Outlier analysis》二三章节的过程中产生的。我没有阅读过其他的书，但是我觉得这本书还是很值得看的。本小节主要介绍在学习到的异常检测的内容。
（针对这本书，后续会专门开设一个专栏来记录每个章节的内容 20201001）
本次阅读过程中，主要学习了这本书的第二和第三章节，分别是：

• Ch2 - Probabilistic and Statistical Models for Outlier Detection
• Ch3 - Linear Models for Outlier Detection

1.1 异常检测算法

在这两个章节中，主要学习一下三部分内容（章节， 模型/方法，具体的重点知识）

• Ch2 基于概率分布的距离测量方法：马哈拉诺比斯距离
• Ch3 线性回归模型：最小二乘法
• Ch3 主成分分析：PCA算法

在学习这些内容的时候，我也感觉到了自己线性代数部分内容的遗忘，直接找了一本同济的那本线性代数的书来看，大致上的概念都能弄懂，但是毕竟也不是完整的学习，肯定是有所缺陷的。

1.2 线性代数的知识

关于线性代数的知识，要讲起来，那就没完了。我捡几个重点，在这部分的学习中，觉得这个东西是最重要的。逆矩阵，特征向量，线性变换。其中线性变换是这个概念一定理解，要知道一个矩阵和向量相乘，在进行线性变换，例如最简单的，[1 0 0 1]，乘以任何一个向量是没有任何变换的。而如果是[1 0 0 0.5]，这个就会把某个向量在y轴上缩小为0.5倍。而且要注意肯定是线性变换。
更深入的，线性变换就是实现了一个变量的旋转和伸缩，而每部分又跟特征向量有关。

注：从后面的章节开始，我就开始讲述针对每个内容的具体，内容较多的话，就会写到另外一篇文章中。而且，在这部分的学习过程中，其实外网上有很多非常有效的文章，我本次学习过程也是主要通过google来实现的。既然有这么多优秀的文章，所以本文将主要记录大致原理，然后记录自己的理解，就不自己推导了，有兴趣的可以直接看原文，当然推荐直接看原文。

2. 马哈拉诺比斯距离

在《Outlier Analysis》的第二小节中，简单介绍了基于统计或者基于概率的方法如何发现异常点。在多元变量分析中，存在四种方法，最后一种就是利用马哈拉诺比斯距离来解决。其他三种方法分别是：基于深度的方法、基于偏差的方法、基于角度的方法，这些方法这里不进行展开。

2.1 具体公式

在单变量的异常检测过程中，使用的方法就是测量某个数值其与均值的距离，然后利用概率分布的方式来测量出来一个异常分数，通常可以假设数据是基于正态分布的。而且有一个点比较重要，就是不管什么类型的方法在进行异常检测，在最后一步，都可以是对每个点或者每个部分设置的异常分数进行划分，此时可以通过基于概率的方法实现最终的检测。而对于多维变量也一样，通过马哈拉诺比斯距离作为整个异常分数。

利用马哈拉诺比斯距离是将数据视为多个混合的高斯分布，概率分布公式为：

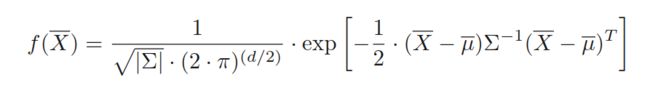
其中$d$为维度，$\Sigma$是相应数据的协方差矩阵。而马哈拉诺比斯距离的具体定义如下：

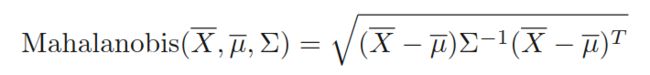
其实，马哈拉诺比斯距离也是基于欧式距离来算的，但是是建立在某种线性代数的转换之上的，这个具体内容后面展开。那么有了上面的公式，利用这个距离方法来测量距离实现异常检测就好了。这里来探讨探讨其深层次的含义。

2.2 马哈拉诺比距离的好处

关于这个距离公式的好处呢，我是将其与欧式距离进行比较，肯定他也有自己的缺陷，但是这里的假设就是，为什么在测量距离的时候，使用这个公式更好呢？其实前面的公式完全是可以通过多变量的正态分布来进行实现的，在测量距离的时候，测量的也是到均值的距离。（我这里的说法有些不贴切，其实利用别的方法来说明更好，例如在使用k近邻的时候，当然这里不再具体展开）我主要说明，马哈拉诺比斯距离解决了欧式距离的什么缺点。以我现在的理解（可能有误），马哈拉诺比斯距离跟欧式距离还是有一定区别的，马哈拉诺比斯距离可能更侧重于在点和分布的距离上，例如前面的公式中，而欧氏距离是更普适的向量空间的距离。

2.2.1 欧式距离的缺点

欧式距离的计算方式很简单，对于两个点$(x_1,y_1),(x_2,y_2)$，他们的欧式距离计算公式如下：
$$distance=\sqrt{(x_1-x_2{)}^2+(y_1-y_2{)}^2}$$
公式简洁明了，在二位平面上就是两个点的直线距离。但是这个公式存在着两个非常大的缺陷。

• 量纲问题
• 变量相关性问题

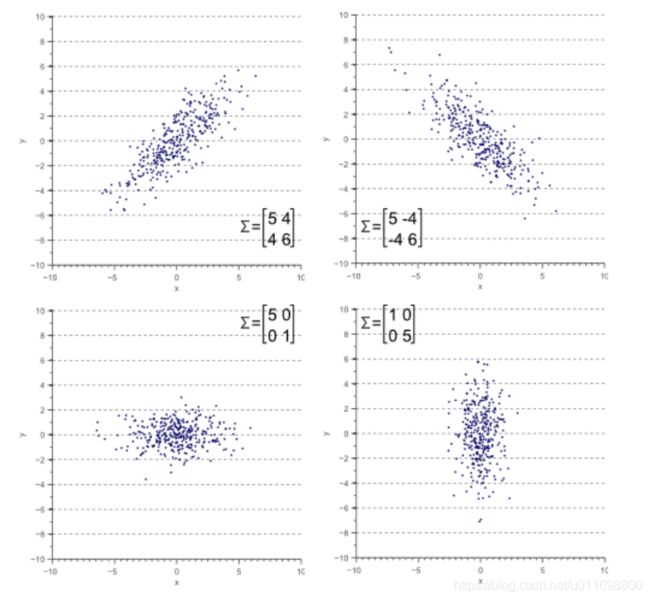
量纲的问题比较明显，当两个数据表中的内容相同，仅仅是量纲不同的时候，可能会发现距离是不同的，但是这个问题比较容易解决，通过最大最小归一化，或者直接正态化都可以，都能从数量上解决距离的问题；但是如果是相关性的话，就不容易解决了。这里先列举一个例子来说明如果是变量之间存在相关会出现什么情况或者说影响。

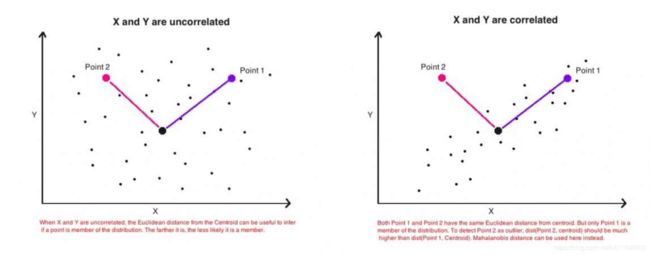
上述图片来源于文章[1]，文章[1]是对马哈拉诺比斯距离的详细介绍，后面还会具体展开。这里先说明相关性的问题。上述图中的两个分布都是二维高斯分布，但是左边式非相关的，右边是相关的。如果是使用欧式距离的话：

• 在不相关的情况下，两个点与高斯分布中心（假设已经进行归一化了）的距离相同时，他们大致的位置应该都是一样的，可以以高斯分布中心画圆。
• 但是在相关的情况下呢，就不对了，假设你要进行异常点检测，上述图中的右图中，点1和点2与中心的距离相同，但是明显点2才是异常点

也就是说，在存在相关的情况下， 欧式距离是不能用来测量这种和中心的距离的，问题就是同样的距离却又不一样的位置，在异常检测中非常受影响。

2.2.2 马哈拉诺比斯距离的好处

在我现在的理解来看，马哈拉诺比斯距离可以解决前面欧式距离在相关性的场景下的问题，他采用的方法是通过对数据进行变换，得到一个某个坐标轴上没有这种相关性。也就是能够再次使用欧式距离的坐标系。通过下面这个图更能说明清楚。

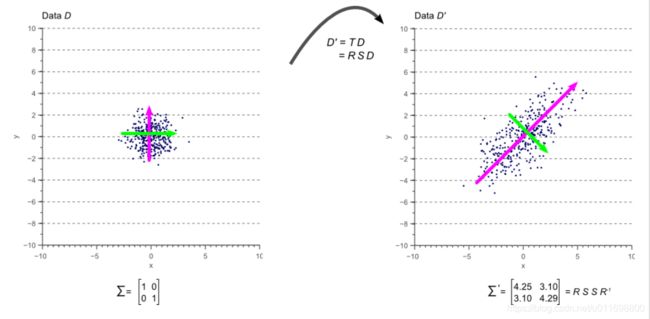
上面这个图片来自于文章[4]，本质上文章[4]是来解释这个协方差矩阵的，但是这里是一致的。也就是说，马哈拉诺诺比斯求解的距离是新的坐标系下面的距离。（注意，实际上马哈拉诺比斯距离是上图的逆过程）。

2.3 马哈拉诺比斯距离的原理解释

2.3.1 具体公式

$$mahalanobisdistance=\sqrt{(X-\mu )C^{-1}(X-\mu {)}^T}$$
其中$X$是数据向量，$\mu$是每列的均值，$C$是协方差矩阵。
上述公式中，两边的东西都无所谓，本质上就是要给加减法的问题，那么重点就来到了这个中间的协方差矩阵的地方。

2.3.2 协方差矩阵

说到协方差，那么首先应该说的是方差，从公式上来看$Var(x)=E((x-E(x){)}^2)$，方差是测量一个随机变量以均值为中心变化的范围。而协方差，所关注的是两个随机变量的关系，一般按照正负分为正相关和负相关，具体公式如下：
$$Var(x,y)=E[(x-E(x))(y-E(y))]$$
协方差矩阵正好是一个对称的矩阵，对角线上是每个变量的方差，而其他的地方是他们两两之间的协方差。用一句简单的话来说，就是衡量一个变量在变化时，另一个变量跟着变化的大小，从而来统计他们的相关性。这里将从矩阵变换的角度来解释协方差矩阵，从而来理解马哈拉诺比斯距离。

上图非常细致了说明了这个协方差矩阵及其在图像上的关系。从图中可以看出，在协方差不等于0的时候，整个点时有一定的相关性的，而且呈现去同时递增或者相反的趋势。上图来自于文章[4]，后续关于协方差矩阵部分的解释，都是来自于原文[4]，阅读原文[4]会更好。
前面已经说到了，欧式距离应用的局限性就是因为由于相关性的问题存在。那么我是不是能找到一个坐标系，在这个坐标系上，他们没有相关性，而原有的方差还存在呢？！其实说到这里，可以想象，直接利用以y为因变量的曲线即可，这是我们从图像上看出来的。那么这个方向应该怎么计算呢？那就又涉及到了特征向量和特征值的问题。也就是说，要对协方差矩阵进行特征向量的分解。
但是在文章[4]中提到，想找到的是方差最大的方向。但是这里我也不是很理解，方差最大的是什么方向，就假如说上方中的第一个图，我们如果是进行数值分解或者什么的，那么肯定应该是拟合出来的直线方向是最大的。但是如果仅仅从协方差矩阵上来看，好像y轴上方差最大，协方差才等于4。但是第二种理解方式肯定是不对的。估计原因就是，通过这种方式得出的结论，还是以x和y为基的空间下的方差。（这是我的理解，暂时不清楚对不对）
而且为什么要找方差最大的？这个也没有具体解释。可能就是因为方差最大的能够变成无关的？！
总之，不管怎么样，我都是要找到一个方向，这个方向上方差最大，那么可以找到一个向量，其方向正好是最大的，而大小是该方向的方差。这里他说的是希望能够找到代表协方差的向量，但是为什么呢？看后面的协方差矩阵的分解部分。

2.3.3 协方差矩阵的特征分解

（这部分内容，我在仔细学习文章[4]的时候，感觉虽然他的结论是对的，但是他这个说理的过程好像是不完备的，具体在什么地方不对，我暂时说不清楚，而且有时候他并没有深入进行解释，另外是有些公式也不是很对的样子。这里先按照他这里的思路往下走吧。）
我们要找到一个向量，这个向量在这个方向上方差最大，可以使用投影的方式。假设这个向量是$v$，然后我的数据是$D$，那么其投影应该是$v^{T}D$，而投影后的数据的方差应该是$v^t\Sigma v$，我们要寻找的这个向量就是能够将上述的方差的数值进行最大化的向量。（前面的公式中，需要严格的推导和定义，他这种形式就跟我在书上见到的不太一样，但大致能理解）
但是对于这个结果的求导，文章[4]并没有给出具体的答案，只是说使用了一个瑞丽商数的东西，直接就能得到这个向量应该是协方差矩阵的特征向量的结果。
（这部分内容后面在PCA中可能还会遇到，这里先简单记下）。

简单总结一下：从前面的说法中可以知道，我要寻找的是一个能够让数据投影之后，方差最大的方向。而通过一定的定理，这个方向正是特征向量的方向。

具体来说，协方差矩阵中方差最大的方向就是特征向量的方向，而且特征值就是方差的大小。~~前面说到了协方差矩阵是对角矩阵的时候，当不是对角矩阵的时候怎么办？此时上面的结论依然存在，只不过他不再是原始的坐标系而已。~~下面来从矩阵变化的形式，来说明以下协方差矩阵的分解。

2.3.4 矩阵变换的实质

在线性代数中，矩阵乘以向量是对向量的线性变换（这部分在线性代数中，多次强调）。而从几何平面上来理解这部分内容，就是对某个向量进行转换，包括旋转和伸缩。关于这部分内容，这里不再进行具体的阐述，可以查看系列视频[3]，一定要看完之后好好思考。
（这里关于具体的线性变换我还是不是非常理解，但是从几何的角度，我基本上能自己想象出来）
同时，再配合上类似空间的基和特征变量这些内容，然后加上几何学的东西，就能大致明白到底是什么意思了。关于这部分，还是需要更多的积累才能明白。知道了这些东西，那么我们可以把协方差矩阵就看作是一种矩阵变换的方式。

先来看一个最简单的例子，如果协方差矩阵是对角矩阵，也就是协方差部分都是0，那么将他应用于不相关的二维单位高斯分布的话。他会发生什么样的变化？

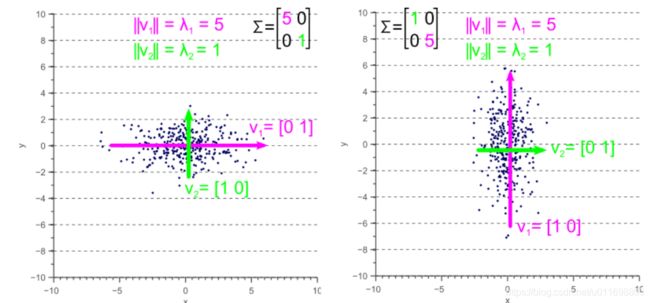
这个图给出的结论比较简单，他属于一种最简单的扩展把，就是在某个方向上进行扩展。那么如果不是对角矩阵呢？如果直接按照视频中[3]的解释，反正就是一种变换嘛，也无所谓。这里细化一下，将这个变换变为两部分（其实这个两部分在视频[3]中也有所体现，就是矩阵乘法的部分）。这两部分分别是旋转和伸缩（两部分肯定是有次序的）。假设我要进行的转换的矩阵是$T$，那么可以将$T$分解为两部分：旋转矩阵$R$和伸缩矩阵$S$，具体公式如下：
$$T=RS$$
其中两个矩阵，又可以分别定义为：
$$R=\left[\begin{array}{cc}cos(\theta )& sin(\theta )\\ sin(\theta )& cos(\theta )\end{array}\right]S=\left[\begin{array}{cc}{s}_x& 0\\ 0& s_y\end{array}\right]$$
其中$\theta$是旋转的角度。

后面将继续分析对协方差矩阵进行分解的内容。前面提到了求解协方差矩阵的特征向量内容，其中$\Sigma v=\lambda v$，那么假设将所有的特征向量都放在一起。
$$\Sigma V=VL$$
其中，$V$每一列都是协方差矩阵$\Sigma$的特征向量，而$L$是对角矩阵，每个值都是特征向量。
那么如此说来的话，可以有以下的结论：
$$\Sigma =VL{V}^{-1}$$
这个方程实际上就是线性代数中的对称矩阵部分的内容。那么既然得到了这样的结论，又跟前面的转换有什么关系呢？其中$V$代表了旋转矩阵，而$\sqrt{L}$是伸缩矩阵。此时就可以看出来，这个东西代表了什么？
$$\Sigma =RSS{R}^{-1}$$
而因为$S$是一个对角矩阵，所以$S=S^T$，而且$R$是一个正交矩阵，那么$R^{-1}=R^T$，因此有以下结论：
$$T=RS，T^T=(RS{)}^T=S^T{R}^T=S{R}^{-1}，\Sigma =RSS{R}^{-1}=T{T}^T$$
那么从上述的内容中可以看出，如果你对某部分数据进行了转换$T=RS$，那么他生成了协方差矩阵就是上面这种形式。再引用一下前面的那张图[4]。

其中方差最大的方向，就是特征值最大的特征向量的方向，剩下的特征向量都和这个最大的特征向量正交。
其实前面的内容实从一种逆向的角度来进行分析，也就是说，我想得到一个协方差矩阵，本质上就是通过这种变换来得到了，分别是旋转和伸缩。而且，最为关键的是，其中旋转的过程中，特征向量就是旋转的方向，而特征值是相应的伸缩范围。而其实特征向量的线性变换，就是利用特征向量和特征值来解释的。前面的分解内容虽然是说针对协方差矩阵来得到，但是实际上如果是普通的矩阵满足要求，也是能够推导出来的。

正如前面所说，这里是一种逆过程，但我们实际上得到的是右边部分的数据，我想要正常的，可以看到前面的马哈拉诺比斯距离的公式，正好带有了协方差矩阵的逆。也就是说，这里就是通过协方差矩阵来获取到了相应的方向，然后得到了距离，正好还是方差最大的方向的距离。

3. 小节

本文主要讲解了在特征变换，或者说在矩阵变换的角度上描述的马哈拉诺比斯距离。但实际上只是从逆过程进行了分析，并没有从正向来理解。

本来是想把所有的内容都写到这一篇文章中，但是发现文章太长了，就分开写。但是本文章已经介绍了非常多的基础的线性代数的内容了，后面更多是运用这些内容的地方。

在马哈拉诺比斯距离的应用过程中，当然不仅仅是这里提到异常检测能用到，肯定还有一些其他的内容能用到，比如说最近邻的分类中，利用马哈拉诺比斯距离来代替欧式距离。

4. 补充

问答[5]通过图像的方式解释了前面大概的意思，本质上你计算的依然是一个欧式距离，只不过是换了一个坐标系统；不顾我这里要说明的问题就是在马哈拉诺比斯距离的推导过程，这部分内容就是来自问答[5]中的一个回答。

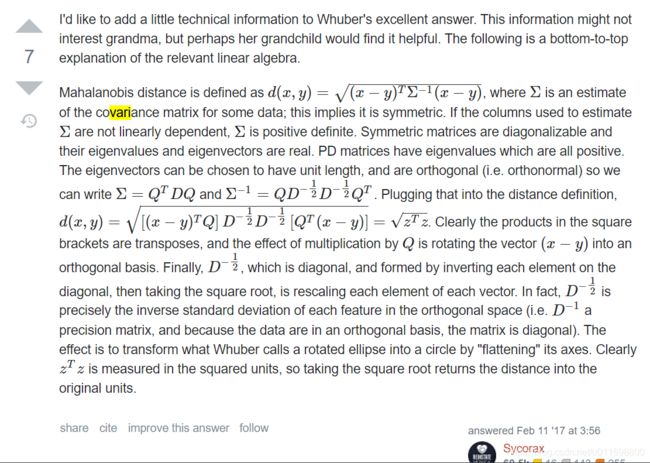
那么具体来说，本来已经知道了$\Sigma =Q^{T}DQ$，当然这个公式是保证的确存在才行，而且和前面的公式有些不一样，但具体含义是一致的。而${\Sigma }^{-1}=Q{D}^{-1/2}{D}^{-1/2}{Q}^T$，将这部分公式代入到马哈拉诺比斯距离公式中（从这里可以看出，他的确是跟前文说的一样，就是一种距离公式）
$$d(x,y)=\sqrt{(x-y{)}^T{\Sigma }^{-1}(x-y)}$$
带入后公式：
$$d(x,y)=\sqrt{[(x-y{)}^{T}Q]D^{-1/2}{D}^{-1/2}[Q^T(x-y)]}=\sqrt{z^{T}z}$$
前面那些操作正好就是之前说的那些旋转和伸缩，这就是的反过程。注意看是${\Sigma }^{-1}$

参考

[1]Mahalonobis Distance – Understanding the math with examples (python)
[2]Baidu（站空用）
[3]【官方双语】线性代数的本质
[4]A geometric interpretation of the covariance matrix
[5]Bottom to top explanation of the Mahalanobis distance?