机器学习基础:模型评估(下)
目录
1. 引言
2. 进一步评估
3. 机器学习中的偏差和方差种类
3.1 过拟合
3.2 欠拟合
3.3 训练曲线观察泛化性
3.4 模型偏差和方差(bias and variance)
3.4.1 偏差 Bias
3.4.2 方差 Variance
3.4.3 方差偏差总结
4. 模型的泛化性(Generalization)
4.1 导致泛化性错误的原因
4.2 诊断高偏差/方差问题
4.2.1 高偏差诊断
4.2.2 高方差诊断
5. 针对偏差和方差的补救措施
6. 评估偏差和方差(Evaluation bias / Variance)
6.1 如何解决Evaluation偏差和方差
1. 引言
在博文《机器学习基础:模型评估(上)》里,我们谈论了模型评估的第一阶段:交叉验证,混淆矩阵,精确度和错误率。
本篇博文进一步的谈论模型评估:
- 如何衡量一个模型是否足够好?
- 什么时候应该停止模型的训练?
- 如何进行超参数的调整?
- 哪几种类型的原因导致模型的表现变差?
- 找出导致模型性能差的原因并进行修正?
2. 进一步评估
除了上面说的那些评估的方法和指标,我们必须还关注模型的:
泛化性:
用来衡量分类器从训练实例中归纳出预测目标函数的能力;如果一个模型的泛化性够好,就代表举一反三的能力强,对于没有见过的样本也能够给出较好的预测。甚至对于相似的数据集也能够给出较好的表现。
一致性:
模型是否可以完美地预测所有训练样本的类别。
3. 机器学习中的偏差和方差种类
偏差种类(偏差 bias 可以代指很多事情):
模型偏差(model bias) 模型能够系统地做出错误预测的倾向 评估偏差(evaluation bias) 评估策略倾向于高估或低估模型有效性的趋势 抽样偏差(sampling bias) 如果训练或评估数据集不能代表总体,就打破了归纳学习假设
方差种类:
- 模型方差(model variance)
- 评估方差(evaluation variance)
泛化性问题,泛化性不好主要体现在两个方面:
- 模型过拟合
- 模型欠拟合
3.1 过拟合
模型太复杂,甚至连数据中的噪声也捕捉了。
过拟合的原因:
- 决策边界很容易被噪声影响;
- 训练集中没有足够多的训练样本支持模型学到整个数据集的分布。
- 另外一种情况就是训练集合测试集在划分的时候没有按照相同的分布(也就是划分数据集的时候采样的随机性不足),在这种情况下,即使训练集样本很多也不能够学到整个数据集的分布,照样会造成过拟合的问题。
决策边界很容易被噪声影响:
如果对于一个简单的模型,遇到图中的![]() 可能没有那么强的能力去拟合,但是如果模型过于复杂,他就有强大的能力连噪声也拟合了,反而导致模型的泛化性不如简单模型。
可能没有那么强的能力去拟合,但是如果模型过于复杂,他就有强大的能力连噪声也拟合了,反而导致模型的泛化性不如简单模型。
训练集中没有足够多的训练样本支持模型学到整个数据集的分布:
如果训练集只有这么几个简单的样本,那么如果在测试集中如果出现了下面的情况:
测试样本中的分布与训练样本中的差距很大,也就是说:模型没有通过训练集学到整个样本集的分布情况;这样也会导致过拟合和模型精度不高的情况。
3.2 欠拟合
模型表达能力不够,无法捕获数据中的潜在的模式。
适当的拟合模型捕捉数据中的基本模式。
3.3 训练曲线观察泛化性
- 通过模型的训练曲线,可以观察模型是否发生了过拟合或者欠拟合的现象。
- 曲线的纵轴(
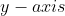 )可以反映模型的精度、错误率或者其他的评估指标
)可以反映模型的精度、错误率或者其他的评估指标 - 曲线的横轴(
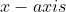 )可以反映例如:训练集大小,模型复杂度,迭代次数
)可以反映例如:训练集大小,模型复杂度,迭代次数
下图展示了一个贝叶斯模型随着训练样本的增加,其训练集精度和验证集精度的变化情况:
最开始的![]() 个样本之前,由于训练集很小,所以在训练集上得到的训练精度很高,而测试集的样本很多,所以验证集的精度比较低,但是随着训练样本的不断增多、测试样本的不断减少,模型训练的越来越充分,因此在测试集上的精度表现越来越好。最后达到模型的收敛状态,训练就可以停止了
个样本之前,由于训练集很小,所以在训练集上得到的训练精度很高,而测试集的样本很多,所以验证集的精度比较低,但是随着训练样本的不断增多、测试样本的不断减少,模型训练的越来越充分,因此在测试集上的精度表现越来越好。最后达到模型的收敛状态,训练就可以停止了
训练集和测试集的比例按照多少划分才比较合适呢?
如果训练的数据太多,就会导致测试集的数据太少从而不能够反映出模型真实的泛化能力;而如果测试集太大导致训练集太小又会导致模型的训练不充分。
为了选择更好的比例对训练集和测试集进行切分,我们可以通过下面的例子来探讨:
Example 1
在下面的例子中,如果让你选择训练集和测试集的切分比例,到底是选
还是
呢:
在这个例子中,其实应该选择![]() 的样本训练,因为
的样本训练,因为![]() 样本用来训练就足以表现的很好了,这种情况下保留更多的测试样本会更加充分地衡量模型的泛化能力。
样本用来训练就足以表现的很好了,这种情况下保留更多的测试样本会更加充分地衡量模型的泛化能力。
Example 2
在线性回归中,我们会使用关于![]() 的多项式来增加线性回归的灵活性,使得模型的拟合能力更加强大,这是因为多项式的引入使得模型的复杂度更高,可以找出更加复杂的内部关系。
的多项式来增加线性回归的灵活性,使得模型的拟合能力更加强大,这是因为多项式的引入使得模型的复杂度更高,可以找出更加复杂的内部关系。
但是从这个图上来看,模型的错误率在多项式的最高次项![]() 之后不降反增,说明了模型的表现其实是在下降。所以模型并不是越复杂越好。
之后不降反增,说明了模型的表现其实是在下降。所以模型并不是越复杂越好。
模型复杂度的问题几乎在所有的模型中都会有超参数进行调整,例如:
- 在深度学习中,神经网络的层数
- 决策树中,决策树的最大深度
3.4 模型偏差和方差(bias and variance)
公式定义:
3.4.1 偏差 Bias
其中![]() 是期望;
是期望;
模型对于某个样本![]() 真实值
真实值![]() 和预测值
和预测值![]() 之间的偏差是
之间的偏差是![]()
数据集中所有![]() 个样本的偏差总和的均值就是 期望偏差
个样本的偏差总和的均值就是 期望偏差![]()
![]() 也可以写成下面这种形式:
也可以写成下面这种形式:
回归任务的![]()
在回归任务中,均方误差可以被用来衡量模型的偏差:
- 对于每个求值实例,都可以计算
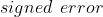 。
。 - 假设每个实例都是独立的,偏差就是这些有符号误差的平均值。
一个模型是有偏差的:如果预测比真实值系统地高,或者预测比真实值系统地低。
一个模型是无偏的:如果预测是系统正确的,或者有些预测太高,有些预测太低。
分类任务![]()
在分类任务的场景中:
- 标签预测不能过高或过低。
- 偏向于多数类意味着我们的模型预测了太多标签为多数类的实例。
通常比较类的分布:
- 无偏差分类器产生的标签具有与实际分布相同的分布
- 有偏差分类器产生的标签分布与实际分布不同
3.4.2 方差 Variance
方差:模型方差是指不同训练集对同一类型的学习者产生不同模型或预测的倾向。
![]() 也是期望;只不过它是对方差的期望。
也是期望;只不过它是对方差的期望。
每个样本的预测值![]() ;所有样本在这个模型下的预测值的期望(均值) 是:
;所有样本在这个模型下的预测值的期望(均值) 是:
由此我们可以得到整个模型的期望方差![]() 是:
是:
一共有![]() 个数据集(标签的类别数一样),在不同数据集上训练的模型表示为
个数据集(标签的类别数一样),在不同数据集上训练的模型表示为![]() 。
。
- 如果一个不同的随机抽样训练集导致评估集上非常不同的预测,那么这个模型就有很大的方差。
- 如果不同的随机抽样训练集导致相似的预测(与预测是否正确无关),则模型的方差较低。
不管预测的对不对,只要在具有相同分布的数据集上,训练出的模型的预测结果是一致的,例如对于![]() 类数据,哪怕全判错成
类数据,哪怕全判错成![]() 类,哪怕都错了,但只要预测的方向一致,模型的方差就低。
类,哪怕都错了,但只要预测的方向一致,模型的方差就低。
3.4.3 方差偏差总结
偏置误差是来自学习算法中错误的假设的误差。高偏差会导致算法错过特征和目标输出之间的相关关系(欠拟合)。
方差是对训练集的小波动的敏感性所产生的误差。高方差可能来自于对训练数据中的随机噪声进行建模的算法(过拟合)。
偏差指的是模型的假设过于简单和真实情况之间的差距,比如一个非线性的数据集,我们使用一个线性的假设,那么这样的假设必然会导致偏差,所以高偏差的数据肯定是欠拟合的。
方差刻画了数据扰动对模型产生的影响,比如相同类型的两个数据集![]() ,他们都包含
,他们都包含![]() 个类别的数据
个类别的数据![]() ,模型
,模型![]() 分别在两个数据集上进行训练,然后用相同的测试集测试,发现模型
分别在两个数据集上进行训练,然后用相同的测试集测试,发现模型![]() 对于样本的判断情况差距很大。例如同样对一个标签为
对于样本的判断情况差距很大。例如同样对一个标签为![]() 的样本,在
的样本,在![]() 上训练的
上训练的![]() 判断成
判断成![]() 而在
而在![]() 上训练的
上训练的![]() 判断成
判断成![]() ,但是在 理想情况下,只要是数据样本类别相同的数据集,无论包含的图片数量多少,使用他们训练出来的模型在同一个测试集上表现应该是一样的。但现在在不同数据集上训练的结果竟然有较大的差距。
,但是在 理想情况下,只要是数据样本类别相同的数据集,无论包含的图片数量多少,使用他们训练出来的模型在同一个测试集上表现应该是一样的。但现在在不同数据集上训练的结果竟然有较大的差距。
但是方差大的模型并不代表就一定过拟合了,因为如果方差和偏差同时高,那就代表这个模型更多地拟合了数据中的噪声。只有方差大偏差小的模型才是过拟合的。
4. 模型的泛化性(Generalization)
一个泛化性好的模型应该对于没见过的样本能够给出很好的预测结果
如何评估一个模型的泛化性能?
给定一个数据集![]() ,假设这个数据集是通过一个函数
,假设这个数据集是通过一个函数![]() 混入一些随机噪声
混入一些随机噪声![]() ,这个随机噪声是一个不可测的误差,可能来自于标注错误等,我们用下列式子表示这个数据集的情况:
,这个随机噪声是一个不可测的误差,可能来自于标注错误等,我们用下列式子表示这个数据集的情况:
![]()
在这种情况下我们对数据集![]() 中的数据进行多次随机采样,得到多个随机采样的子数据集,然后在这些子数据集上训练不同的模型,将他们在验证集上进行验证得到预测结果
中的数据进行多次随机采样,得到多个随机采样的子数据集,然后在这些子数据集上训练不同的模型,将他们在验证集上进行验证得到预测结果![]() ,真实的情况用红线和
,真实的情况用红线和![]() 表示,多个子训练集预测的情况及对应模型用黄线和
表示,多个子训练集预测的情况及对应模型用黄线和![]() 来表示:
来表示:
对于一个模型的误差问题,在之前的部分讲到了![]() 和
和![]() ,还有一个很重要的部分就是随机误差:
,还有一个很重要的部分就是随机误差:
模型的泛化误差有![]() ,
,![]() 和
和![]() 误差三部分构成。
误差三部分构成。
方差:如果你在不同的训练集上训练,你的模型会有多大变化。你的分类器对某一特定训练集的过度专业化程度如何?
偏差:即使有无限的训练数据,你从你的模型中得到的固有误差是多少?这是由于你的模型偏向于某种特定的解决方案。换句话说,偏见是你的模型所固有的。
噪声:这种误差衡量的是由于你的数据分布和特征表示而产生的模糊性。你永远无法战胜它;它是数据的一个方面。
衡量了在不同数据集上训练的模型对于同一个测试集的表现差异
反映了模型的假设在多大程度上和数据的真实情况是相符的,即有没有在构建模型的时候对数据进行较为准确的假设。
是一种不可避免的由数据分布和特征等很多方面的综合表示而造成的误差
4.1 导致泛化性错误的原因
高偏差和高方差都可以导致模型的泛化性很差:
 模型的方差为
模型的方差为 ,但是偏差很高。
,但是偏差很高。- 一个很复杂的模型可能偏差很低但是方差很高。
拥有低偏差和低方差的模型被认为是泛化性能好的模型。
4.2 诊断高偏差/方差问题
从根本上说,处理偏差和方差其实就是处理过拟合和欠拟合。偏差减少,方差增加与模型的复杂性有关。
下面展示的是方差和偏差随着模型复杂度的变化:
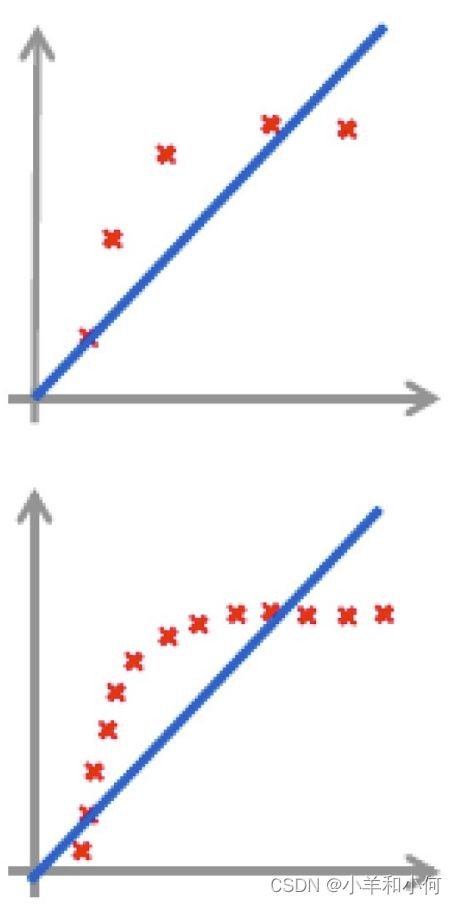
下图展示的是训练样本数量与![]() 的变化关系:这三个图分别表示了欠拟合(高偏差),过拟合(高方差低偏差),以及一个泛化性较好的模型。
的变化关系:这三个图分别表示了欠拟合(高偏差),过拟合(高方差低偏差),以及一个泛化性较好的模型。
4.2.1 高偏差诊断
增加训练集的规模对于![]() 小的模型并不会有什么帮助,下图红色点是训练集的样本,蓝色线是拟合出的高
小的模型并不会有什么帮助,下图红色点是训练集的样本,蓝色线是拟合出的高![]() 模型。
模型。
高![]() 的学习曲线特点是训练误差和测试误差都大。
的学习曲线特点是训练误差和测试误差都大。
4.2.2 高方差诊断
使用更多的样本进行训练可以缓解高方差的问题,因为训练样本越大,分布就越接近理想分布,方差就能够有效减小。
高方差的学习曲线特征是![]() 和
和![]() 之间存在差距。
之间存在差距。
5. 针对偏差和方差的补救措施
高偏差补救措施
- 采用更复杂的模型(例如非线性模型)。
- 增加训练模型所使用的特征数量。
- 使用
集成方法不断地对模型的残差进行迭代学习。
集成:
- 训练数据:不同的权重(要选择的概率)
- 使用多个弱模型
一个更强的模型;减少偏差(提高性能)
- 使用多个弱分类器。
- 按照顺序,前一个弱分类器学习产生的误差由后一个弱分类器来学习,即每个弱分类器都只学习前一个弱分类器的误差。
- 最后按照权重将这些顺序的弱分类器进行整合得到一个强分类器。
- 这样的方式相当于不断地增加模型的复杂度,提高对数据的拟合能力,从而减小偏差。
高偏差补救措施
- 增加更多的训练数据
- 减少构建模型时使用的特征数量
- 减小模型训练的复杂度
- 采用正则化方法(
)
的方式进行模型集成
![]()
例如在 SVM 模型中,调整正则化参数 C 来控制对落在决策边界中的样本的严苛程度。
![]() 集成
集成
- 从原始数据集中构建新数据集: 随机有放回地选取训练数据,构造多个新数据集。
- 结合多个不同的模型常用投票法来集成,可以减少模型的方差。
6. 评估偏差和方差(Evaluation bias / Variance)
偏差和方差的定义:
- 评估的质量与模型无关,只与评估的方法有关
- 如果有无限大的测试集,那么在这个测试集上表现出的测试精度才能完全反映当前模型的训练情况。
评估结果可能存在的问题:
- 对于某些特定的
,模型有很好的精度,但是对于其他不可见的
,模型的精度很差。
- 评估函数(
)也有可能对验证数据(
)过拟合。
我们想要知道一个分类器的“真实”错误率,但是我们只对错误率进行了估计,这取决于一些特定的评估样本集(因为没办法获得无穷大的测试样本集)。
评估偏差(evaluation bias):我们对于模型的评估是偏颇的; 我们对模型有效性的估计系统地过高/过低。
评估方差(evaluation variance):当我们改变 测试集 中的样本时(采用不同的测试样本集),我们对模型有效性的估计会改变很多。
6.1 如何解决Evaluation偏差和方差
合理的划分训练测试集:训练集越大测试集越小——训练方差会更小,测试方差会更大。
重复随机采样(repeated random subsampling)和交叉验证(cross-evaluation)可以得到更小的模型方差和评估方差。
分层采样(stratification) / 垂直采样(vertical sampling):有效降低模型和评估的偏差。
留一法交叉验证(leave-one-out Cross validation):消除了采样偏差(sampling bias),通常也有最低的偏差/方差。











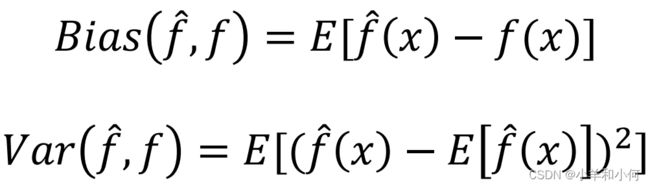


![E[\hat{f}(x)]=\frac{1}{n}\sum_{i=1}^n\hat{f}(x_i)](http://img.e-com-net.com/image/info8/d819dce46303471ab166e5392b4efa1c.gif)
![Var(\hat{f},f)=E[(\hat{f}(x_i)-E[\hat{f}(x_i)])^2]=\frac{1}{m}\sum_{j=1}^m(\hat{f_j}(x_i)-\frac{1}{n}\sum_{i=1}^n\hat{f_j}(x_i))^2](http://img.e-com-net.com/image/info8/d784a55f85ec43ef93bcad3f84756bed.gif)