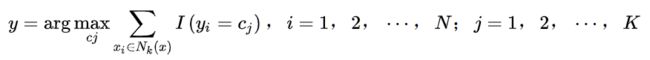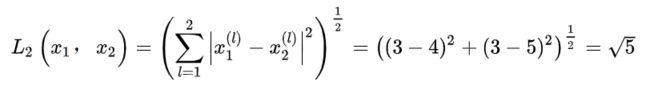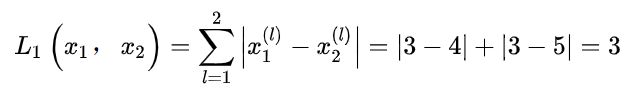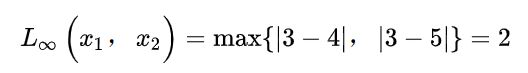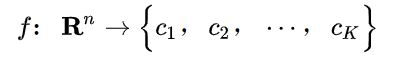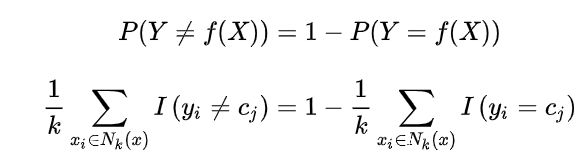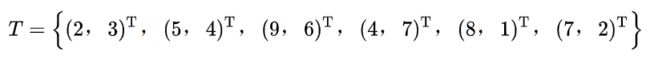k近邻(KNN)模型详细解读 | 统计学习方法学习笔记 | 数据分析 | 机器学习
目录
1.走近k近邻 - 你周围的人决定了你是怎样的人:
2.重要概念:
3.k近邻算法的数学形式:
4.k近邻模型的直观认识:
5.如何计算距离:
6.k值的选择:
7.k近邻算法的损失函数:
8. kd树数据结构:
9.搜索kd树:
KNN模型Python复现,使用了线性扫描;权值优化两种算法:
舟晓南:k近邻(KNN)模型python复现 - 线性扫描;带权值的近邻点优化方法![]() https://zhuanlan.zhihu.com/p/258076346
https://zhuanlan.zhihu.com/p/258076346
1.走近k近邻 - 你周围的人决定了你是怎样的人:
人是群居动物,这不仅是因为整个社会运转需要各种各样的人才进行劳动分工和资源交换,还因为人本性上需要认同感,不仅是身份认同,还希望对他的行事风格的,性格的,爱好的,外表的等等方面的认同。
基于这点,大部分的人类个体都会在生活中逐渐与一群于自己相似的人类个体组成一个个圈子,我们可以将这个圈子认为是一个类。
而在这个圈子里,不说全部,至少绝大部分的人类个体都会有共同点,这些共同点,就可以用来判断一个新来的人最有可能被哪一个圈子所接受,或者他最有可能长久地加入哪个圈子,这就是分类。
人是群居动物
这其实就是近朱者赤,近墨者黑的思想,但在k近邻算法中,我们并不关心到底是因为他本来就是赤的所以近朱,还是因为他近墨而变黑,我们也不关心他的变化过程,我们只关心当前状态下,可以将他分类为赤者,还是黑者。
在明白k近邻算法的大致思路后,我们需要了解它的数学形式。
2.重要概念:
在正式介绍k近邻模型之前,需要先对一些基本概念有所了解,如果明白这些概念可以直接跳过。
泛化能力:指通过机器学习获得模型后,该模型对新输入的实例进行正确预测的能力。如果在学习模型中,仅使用了相同的验证集来验证模型,那么在对模型不断的改进中的参照物实际上就是一个不变的验证集,因此训练出来的模型可能仅对这个特定的验证集的预测能力较高,但对新的数据集的预测能力较差,这就是所谓的泛化能力低。
近似误差:更关注于训练集。当新输入的实例更依赖于训练集进行预测,则近似误差较小,也就是对训练集的预测较好,但该预测仅仅是依据训练集而言,其泛化能力可能比较差。
估计误差:更关注于模型的泛化能力。模型泛化能力越强,其估计误差越低,但是往往这样的模型的近似误差较高。
噪声:被错误标记的实例,或者数据的波动。噪声对过于依赖训练集的模型影响非常大,因为这样训练出来的模型将训练集中的噪声也考虑了进去,而在新的需要进行预测的数据集中的噪声与训练集中的噪声并不一样,所以这样的模型泛化能力较弱。换一种给说法就是这种算法或模型对噪声敏感。
过拟合:训练集中难免会产生噪声,如果一个模型将训练集中的噪声也进行了学习,该模型对新数据的预测的表现会很差,这个情况称为过拟合。
欠拟合:欠拟合是指模型对训练集的预测和对新的数据的预测都表现不好的情况。
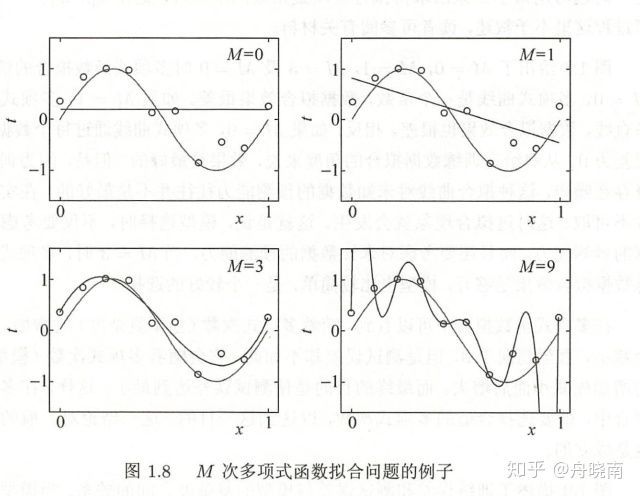
下图中,M代表拟合多项式的次数,当M=0和1时都产生了欠拟合,当M=9时产生了过拟合,当M=3时,其拟合程度较好。
交叉验证:一种常用的模型选择方法。在训练集数据充足的情况下,将训练集随机地切分成三个部分,分别为新的训练集、验证集和测试集。训练集用来训练模型,验证集用于模型的选择,而测试集用于最终对模型的评估。对多个模型而言,可以选择对验证集有最小预测误差的模型。
如果数据量并不充足,可以采用交叉验证方法。交叉验证的基本想法是重复地使用数据,比如将数据随机切分成A,B,C,D,E五组,使用其中的四组进行模型的训练,用剩下的一组对模型进行验证。验证完成后,再用不同的四组组合成新的训练集,用剩下的另一组验证模型。这一过程重复进行5次,即A,B,C,D,E轮流作为验证集使用。
当然,我们也可以将数据集切分成不同数量的组,这种交叉验证的方法被称作S折交叉验证,S代表数据集被切分后的组数,比如上面提到的为5折交叉验证。
多数表决:一种分类依据,比如对新输入实例有三个表决认为应该归为A类,五个表决认为应该归为B类,则将该实例归为B类。
经验风险:模型关于训练集的平均损失。
3.k近邻算法的数学形式:
给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的k个实例,这k个实例的多数属于某个类,就把该输入实例分为这个类。
过程:
(1) 根据给定的距离度量,在训练集T中找出与最邻近的k个点,涵盖这k个点的x的邻域记作Nk(x)。
(2) 在Nk(x)中根据分类决策规则(如多数表决)决定x的类别y。
数学表达如下:
I为指示函数,即当yi=cj时I为1,否则为0。N是x的邻域中实例的数量,Cj是某一种类别,K是实例种类的数量。
上式用文字描述为,在邻域内遍历每个样本点,并得到分到每个类别的样本点的个数,个数最多的类别认为是新输入实例y的类别。
需要指出的是,对于领域的定义根据对距离的定义不同而改变,距离定义比较常见的有欧式距离和曼哈顿距离等,接下来会在如何计算距离这一节中谈到这一点。
4.k近邻模型的直观认识:
k近邻法中,当训练集、距离度量(如欧氏距离)、k值(近邻点的数量)及分类决策规则(如多数表决)确定后,对于任何一个新的输入实例,它所属的类可以被确定并且为唯一的类。
特征空间中,对每个训练实例点x,距离该点比其他点更近的所有点(这里指特征空间中的所有点,而非单指实例点)组成一个区域,叫作单元。每个训练实例点拥有一个单元,所有训练实例点的单元构成对特征空间的一个划分。
在该实例点对应的单元中的每个点都被归为该实例点的类中。如果有一个新的实例点落入某一单元内,则该点被划分为这个单元所对应的类中。
接下来讲解如何确定训练集实例与新输入实例之间的距离。
5.如何计算距离:
k近邻模型的特征空间一般是n维实数向量空间Rn。使用的距离是欧氏距离,但也可以是其他距离,如更一般的L距离或Minkowski距离。
对于两点xi,xj之间的距离的一般公式可以用Lp定义:
其中p为距离公式的参数,xi和xj都是n维特征空间中的向量:
举例来说,对于在二维特征空间中的两个实例x1(3,3),x2(4,5):
当p=2时,称为欧氏距离。
当p=1时,称为曼哈顿距离。
当p=∞时,它是各个坐标距离的最大值。
下图代表在二维空间中p取不同值时,与原点的L距离为1的点围成的图形
在k近邻算法中,我们通常采用欧氏距离。我们有了距离之后,还需要决定到底要考虑多少个点来决定新输入实例的类,也就是k值到底选多大比较合适。
6.k值的选择:
k代表与新的输入实例距离最近的实例的数量。
如果选择较小的k值,就相当于用较小的邻域中的训练实例进行预测,“学习”的近似误差会减小,只有与输入实例较近的训练实例才会对预测结果起作用。但缺点是“学习”的估计误差会增大。预测结果会对近邻的实例点非常敏感,而远处的实例点则对此没有影响,如果邻近的实例点恰巧是噪声,预测就会出错。
k值的减小就意味着整体模型变得复杂,容易发生过拟合。
如果选择较大的k值,就相当于用较大邻域中的训练实例进行预测。其优点是可以减少学习的估计误差,但缺点是学习的近似误差会增大。这时与输入实例较远的训练实例也会对预测起作用,使预测发生错误。k值的增大就意味着整体的模型变得简单,容易发生欠拟合。
在应用中,k值一般取一个比较小的数值。通常采用交叉验证法来选取最优的k值。
在了解了如何选择k值的方法后,我们需要一个具体的数值来代表不同的k对应的模型的好坏,也就是损失函数。接下来讲解k近邻算法的损失函数。
7.k近邻算法的损失函数:
k近邻法中的分类决策规则往往是多数表决,即由输入实例的k个邻近的训练实例中的多数类决定输入实例的类。
多数表决有如下解释:如果分类的损失函数为0-1损失函数(即分类错误则为1,分类正确则为0,要极小化该损失函数,让分类错误的数量下降),分类函数为:
即共有K个类。
那么,误分类的概率 =(1 - 正确分类的概率):
其中I是指示函数。
要使误分类率最小即经验风险最小,就要使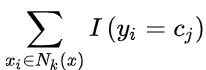 最大,所以多数表决规则等价于经验风险最小化,因为多数表决使得正确分类的个数最大化,而经验风险最小化是使被误分类的个数最小化,两者等价。
最大,所以多数表决规则等价于经验风险最小化,因为多数表决使得正确分类的个数最大化,而经验风险最小化是使被误分类的个数最小化,两者等价。
就像上一节所说,可以通过交叉验证法选择最合适的k值,具体就是对多个k值训练多个模型,然后通过交叉验证法找到经验风险最小的k值,就是最优k值。
现在有了选择k值的具体方法,但是在实际应用中,如果实例数量很多,计算每个新输入实例与每个训练实例的距离,再选择其中与各个输入实例较近的k个训练实例(这种暴力的方法叫做线性扫描),将消耗大量算力和时间。那么有没有提高计算效率的方法呢?答案就是采用kd树数据结构对数据进行存储(并非唯一的方法,这里仅参照《统计学习方法》讲解该法)。
8. kd树数据结构:
具体的kd树方面的知识需要专门学习数据结构,在《统计学习方法》这本书中仅是简单地介绍了以下kd树的构造和搜索方法和原理。
构造kd树的方法如下:
(1) 构造根结点:在特征空间中选择一个维度,选择所有实例在该维度上的中位数作为切分点,将特征空间分割为两个部分。
(2) 生成子结点:在分割出来的两个子空间中选择在当前维度小于切分点的子空间,并选择另一个维度,按照1的方法确定切分点,将该子区域再次分割为两个部分,并将该切分点对应的实例特征存储在左子结点。如果选择当前维度大于切分点的子空间,则把新的切分点对应实例特征存储在右子结点。
(3) 重复步骤2,直到特征空间中的子空间中不存在实例点。
注意:
(1) 通常,依次选择坐标轴对空间切分。
(2) 如果样本点数量为偶数,数学上中位数应当是中间两个数的平均值,但在kd树中一个结点不能为空,因此可以选择中间两个数中的一个作为切分点。
(3) 按照上述方法得到的kd树是平衡的,但平衡的kd树搜索时的效率未必是最优的。所谓平衡树,是指左右子树的高度相差不超过 1 的树。
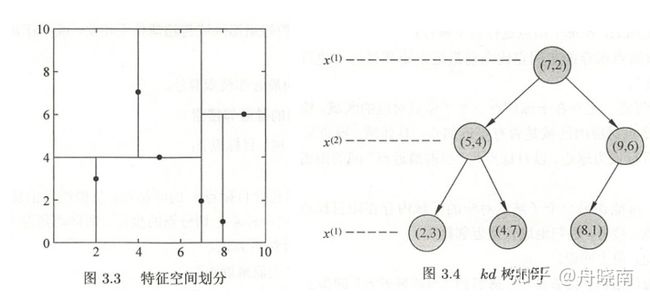
现在举一个书中的例子,方便更好理解:
对以下实例建立kd树:
首先选择横轴作为切分轴,我们将所有实例的横轴坐标从小到大排列为(2, 4, 5, 7, 8, 9),那么中位数应该是(5+7)/2 = 6,但因为没有实例点的横坐标为6,而kd树中不能存在空结点,于是采用5或7为切分点,这里采用7为切分点,对应的根结点为(7,2)。
接着在切分的子空间中,都选择竖轴作为切分轴,左空间的中位数是4,右空间的中位数是6,因此根结点左边的子结点存储(5,4),右节点存储(9,6),以此类推,得到图中的kd树。
可以看到对于根节点而言,左子树高度为2,右子树高度也为2,高度差为0。对于(5,4)这个结点来说,左右高度差为0。对于(9,6)来说,左右高度差为1,不超过1。因此该树是平衡树。
kd树建立完成后,在预测过程中我们需要对存储在树中的数据进行访问,接下来解释如何对kd树进行搜索。
9.搜索kd树:
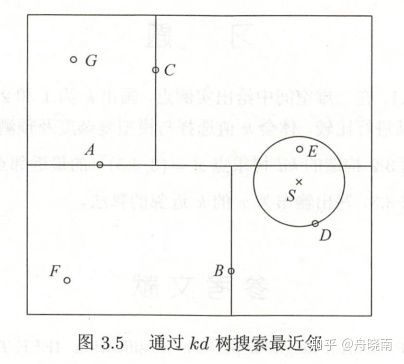
第一步:从根结点出发,递归地向下访问kd树。若实例点S的坐标在当前维小于切分点,则向左访问,反之,向右访问,直到访问到叶节点,取该叶节点作为包含S的结点。
在上图中,根结点为A,在竖轴,S的坐标小于A,则访问左子结点B,在横轴,S的坐标大于B,则访问B的右子结点D,D是叶节点,则选取D作为包含S的叶节点,即当前最近点。
图中,以S为圆心,SD为半径画圆,真正的最近邻点应该在该圆内或圆周上。对于更多维的特征空间,我们称此圆为超球体。
第二步:从当前最近点回退该点所属的父结点,访问父结点的另一个分支,查看该子空间是否与超球体相交,即检查是否有结点比当前最近点与S距离更近。若有,则选择该点作为新的当前最近点,若没有,则回退kd树上一层的父结点。
图中,回退D的父结点B,检查结点B的另一个子结点F,F距离更远,回退父结点A,检查A的另一个子结点C的区域,发现点E在圆内,且比D更近,设置E为新的当前最近点。
第三步:回退到根结点,搜索结束,当前最近点即为最近邻点。
图中,回退C的父结点A,即根结点,搜索结束,最近邻点为E。
同名公众号和知乎:舟晓南
对机器学习,深度学习,python感兴趣,欢迎关注专栏,学习笔记已原创70+篇,持续更新中~ ^_^
学习笔记:数据分析,机器学习,深度学习![]() https://www.zhihu.com/column/c_1274454587772915712
https://www.zhihu.com/column/c_1274454587772915712
专栏文章举例:
【机器学习】关于逻辑斯蒂回归,看这一篇就够了!解答绝大部分关于逻辑斯蒂回归的常见问题,以及代码实现 - 知乎 (zhihu.com)
关于 python 二三事![]() https://www.zhihu.com/column/c_1484952401395941377
https://www.zhihu.com/column/c_1484952401395941377
专栏文章举例:
记录一下工作中用到的少有人知的pandas骚操作,提升工作效率 - 知乎 (zhihu.com)
关于切片时不考虑最后一个元素以及为什么从0开始计数的问题 - 知乎 (zhihu.com)
关于转行:
舟晓南:如何转行和学习数据分析 | 工科生三个月成功转行数据分析心得浅谈
舟晓南:求职数据分析师岗位,简历应该如何写?|工科生三个月成功转行数据分析心得浅谈
我建了个数据分析,机器学习,深度学习的群~ 需要学习资料,想要加入社群均可私信~
在群里我会不定期分享各种数据分析相关资源,技能学习技巧和经验等等~
详情私信,一起进步吧!