自注意力机制中的位置编码
本内容主要介绍自注意力(Self-Attention)机制中的位置编码。
1.1 为什么自注意力机制需要位置编码
1.1.1 自注意机制简介
Google 在 Transformer 论文 Attention Is All You Need 中提出了自注意力机制。
当一个有 n n n 个元素的序列 x = ( x 1 , ⋯ , x n ) x=(x_1,\cdots,x_n) x=(x1,⋯,xn) 输入进一个自注意力模块时,需要计算一个新的序列 z = ( z 1 , ⋯ , z n ) z=(z_1,\cdots,z_n) z=(z1,⋯,zn)。元素 z i z_i zi 为输入元素线性变换后的加权和:
z i = ∑ j = 1 n α i j ( x j W V ) (1.1) z_i = \sum_{j=1}^n \alpha_{ij} (x_j W^V) \tag{1.1} zi=j=1∑nαij(xjWV)(1.1)
其中,权重系数 α i j \alpha_{ij} αij 由 Softmax 函数计算得到:
α i j = softmax ( e i j ) = exp e i j ∑ k = 1 n exp e i k (1.2) \alpha_{ij} = \text{softmax}(e_{ij}) = \frac{\exp{e_{ij}}}{\sum_{k=1}^n \exp{e_{ik}}} \tag{1.2} αij=softmax(eij)=∑k=1nexpeikexpeij(1.2)
其中,参数 e i j e_{ij} eij 由两个输入元素计算得到:
e i j = ( x i W Q ) ( x j W K ) T d (1.3) e_{ij} = \frac{(x_iW^Q)(x_jW^K)^T}{\sqrt{d}} \tag{1.3} eij=d(xiWQ)(xjWK)T(1.3)
上面公式中的 W Q W^Q WQ, W K W^K WK 和 W V W^V WV 是可训练的参数矩阵。

1.1.2 为什么自注意力机制需要位置编码
在一个句子里,各个词的前后关系对这个句子的意义是有影响的,这种影响不仅体现在语法方面,而且还体现在语义方面。
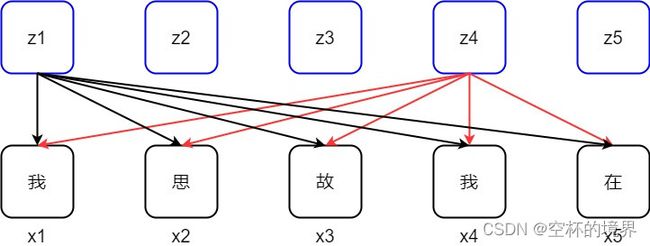
从上一小节自注意力机制简介中,我们知道当一个序列输入进一个自注意力模块时,由于序列中所有的 Token 是同时进入并被处理的,如果不提供位置信息,那么这个序列的相同的 Token 对自注意力模块来说就不会有语法和语义上的差别,他们会产生相同的输出。比如,图 1.2 里的词 “我” 出现 2 次,它们的初始表达向量是一样的,如果不加入位置信息,那么自注意力模块产生的对它们的关注度是一样的,或者模型产生的新的表达式一样的。所以,我们需要在输入序列里人为加入每个 token 的位置信息。
1.2 位置编码
为了给自注意力模块加入位置编码,我们大体有两中选择:
-
想办法将位置信息融入到输入中,这构成了绝对位置编码的一般做法。
-
想办法微调一下 Attention 结构,使得它有能力分辨不同位置的 Token,这构成了相对位置编码的一般做法。
1.2.1 绝对位置编码
形式上来看,绝对位置编码是相对简单的一种方案。一般来说,绝对位置编码会加到输入中:在输入的第 k k k 个向量 x k x_k xk 中加入位置向量 p k p_k pk 变为 x k + p k x_k+p_k xk+pk,其中 p k p_k pk 只依赖于位置编号 k k k。
那么式(1.1)和(1.3)分别修改为:
z i = ∑ j = 1 n α i j ( ( x j + p j ) W V ) (1.4) z_i = \sum_{j=1}^n \alpha_{ij} ((x_j+p_j) W^V) \tag{1.4} zi=j=1∑nαij((xj+pj)WV)(1.4)
e i j = ( ( x i + p i ) W Q ) ( ( x j + p j ) W K ) T d (1.5) e_{ij} = \frac{((x_i+p_i)W^Q)((x_j+p_j)W^K)^T}{\sqrt{d}} \tag{1.5} eij=d((xi+pi)WQ)((xj+pj)WK)T(1.5)
1.2.1.1 Transformer 中的静态绝对位置编码
Google 在 Transformer 论文 Attention Is All You Need 中提出:
{ p k , 2 i = sin ( k / 1000 0 2 i / d ) p k , 2 i + 1 = cos ( k / 1000 0 2 i / d ) (1.6) \left \{ \begin{array}{cc} \begin{aligned} &p_{k,2i} = \sin(k/10000^{2i/d}) \\ &p_{k,2i+1} = \cos(k/10000^{2i/d}) \end{aligned} \end{array} \right. \tag{1.6} {pk,2i=sin(k/100002i/d)pk,2i+1=cos(k/100002i/d)(1.6)
其中, p k , 2 i p_{k,2i} pk,2i 和 p k , 2 i + 1 p_{k,2i+1} pk,2i+1 分别是位置 k k k 的编码向量的第 2 i 2i 2i 和 2 i + 1 2i+1 2i+1 个分量, d d d 是位置向量的维度。
1.2.1.2 BERT 中的动态绝对位置编码
BERT 使用了绝对位置动态编码。其位置编码向量由一个 L × d L \times d L×d 的矩阵提供(其中 L L L 是序列长度, d d d 为词嵌入维度),其通过训练产生。
1.2.2 相对位置编码
顾名思义,这种编码是以输入序列的一个位置为参考点,为离这个位置的距离进行编码,而绝对位置编码是为每个位置进行编码。
1.2.2.1 经典相对位置编码
Google 在论文 Self-Attention with Relative Position Representations 中提出了一种相对位置编码。引入了两个训练向量 a i j V , a i j K a_{ij}^V,a_{ij}^K aijV,aijK 用来学习两个输入元素 x i x_i xi 和 x j x_j xj 之间的相对位置表示,这两个向量在每层的各个注意力头之间共享。
首先,将式(1.1)修改为:
z i = ∑ j = 1 n α i j ( x j W V + a i j V ) (1.7) z_i = \sum_{j=1}^n \alpha_{ij} (x_j W^V + a_{ij}^V) \tag{1.7} zi=j=1∑nαij(xjWV+aijV)(1.7)
然后,将式(1.3)修改为:
e i j = ( x i W Q ) ( x j W K + a i j K ) T d z (1.8) e_{ij} = \frac{(x_i W^Q)(x_j W^K + a_{ij}^K)^T}{\sqrt{d_z}} \tag{1.8} eij=dz(xiWQ)(xjWK+aijK)T(1.8)
一般认为,距离过远的词之间在语法和语义上的关联很弱了,可以不考虑。这样,我们定义一个截断距离 k k k,因此只需要考虑 2 k + 1 2k+1 2k+1 个相对位置编码。这样做,还有一个好处,模型可以很好的扩展到训练期间没遇到的序列长度。
a i j K = w clip ( j − i , k ) K a i j V = w clip ( j − i , k ) V clip ( x , k ) = max ( − k , min ( k , x ) ) (1.9) \begin{array}{cc} a_{ij}^K = w_{\text{clip}(j-i,k)}^K \\ a_{ij}^V = w_{\text{clip}(j-i,k)}^V \\ \text{clip}(x,k) = \max(-k, \min(k,x)) \end{array} \tag{1.9} aijK=wclip(j−i,k)KaijV=wclip(j−i,k)Vclip(x,k)=max(−k,min(k,x))(1.9)
然后我们学习相对位置表示 w K = ( w − k K , ⋯ , w k K ) w^K = (w_{-k}^K,\cdots,w_k^K) wK=(w−kK,⋯,wkK) 和 w V = ( w − k V , ⋯ , w k V ) w^V = (w_{-k}^V,\cdots,w_k^V) wV=(w−kV,⋯,wkV),其中 w i K , W i V ∈ R d a w_i^K,W_i^V \in \mathbb{R}^{d_a} wiK,WiV∈Rda。从上面可以看到 a i j V , a i j K a_{ij}^V,a_{ij}^K aijV,aijK 依赖于相对距离 j − i j-i j−i。
小结:一个长度为 L L L 的序列,相对位置最多有 2 L − 1 2L-1 2L−1 个。如果设置了截断距离 k k k,那么相对位置的数量就变成 2 k + 1 2k+1 2k+1,我们要为这些相对位置构建维度为 d d d 的相对位置编码。我们以可训练的变量形式创建大小为 ( 2 k + 1 ) × d (2k+1) \times d (2k+1)×d 的相对位置编码矩阵 P P P,以及为每对词之间的相对距离创建大小为 L × L L \times L L×L 的相对距离矩阵 D D D。然后,以 D D D 矩阵里的元素值 d i j d_{ij} dij(即相对距离)为行索引,在 P P P 矩阵里抓取一行作为词 j j j 相对词 i i i 的相对位置编码向量 p i j K p_{ij}^K pijK,再把这个位置编码向量作为偏置向量加到词 j j j 的 Key 向量上,与自注意力模块一起训练即可。为 Value 向量创建的相对位置编码向量 p i j V p_{ij}^V pijV 也是同样的过程。
1.2.2.2 Transformer-XL 和 XLNet 中的相对位置编码
Transformer-XL 和 XLNet 的相对位置编码借鉴了经典相对位置编码,然后在绝对位置编码式(1.5)的基础上做了若干变化,从而得到最终的公式。
首先,将式(1.5)的分子部分展开(在这里,我们不考虑分母的 d \sqrt{d} d,因为其对分析结果不会产生影响),得到:
A i , j abs = x i W Q W K ⊤ x j ⊤ ⏟ ( a ) + x i W Q ( W K ) ⊤ p j ⊤ ⏟ ( b ) + p i W Q ( W K ) ⊤ x j ⊤ ⏟ ( c ) + p i W Q ( W K ) ⊤ p j ⊤ ⏟ ( d ) (1.10) \begin{aligned} \text{A}_{i,j}^{\text{abs}} =&\underbrace{x_iW^Q {W^K}^\top x_j^\top}_{(a)} +\underbrace{x_iW^Q (W^K)^\top p_j^\top}_{(b)} \\ &+\underbrace{p_iW^Q (W^K)^\top x_j^\top}_{(c)} +\underbrace{p_iW^Q (W^K)^\top p_j^\top}_{(d)} \end{aligned} \tag{1.10} Ai,jabs=(a) xiWQWK⊤xj⊤+(b) xiWQ(WK)⊤pj⊤+(c) piWQ(WK)⊤xj⊤+(d) piWQ(WK)⊤pj⊤(1.10)
然后,对上式做一些变化,得到:
A i , j abs = x i W Q ( W K , E ) ⊤ x j ⊤ ⏟ ( a ) + x i W Q ( W K , R ) ⊤ r i − j ⊤ ⏟ ( b ) + u ( W K , E ) ⊤ x j ⊤ ⏟ ( c ) + v ( W K , R ) ⊤ r i − j ⊤ ⏟ ( d ) (1.11) \begin{aligned} \text{A}_{i,j}^{\text{abs}} =&\underbrace{x_iW^Q (\textcolor{green}{W^{K,E}})^\top x_j^\top}_{(a)} +\underbrace{x_iW^Q (\textcolor{green}{W^{K,R}})^\top \textcolor{blue}{r_{i-j}^\top}}_{(b)} \\ &+\underbrace{\textcolor{red}{u} (\textcolor{green}{W^{K,E}})^\top x_j^\top}_{(c)} +\underbrace{\textcolor{red}{v} (\textcolor{green}{W^{K,R}})^\top \textcolor{blue}{r_{i-j}^\top}}_{(d)} \end{aligned} \tag{1.11} Ai,jabs=(a) xiWQ(WK,E)⊤xj⊤+(b) xiWQ(WK,R)⊤ri−j⊤+(c) u(WK,E)⊤xj⊤+(d) v(WK,R)⊤ri−j⊤(1.11)
-
首先,是(b)和(d)中的绝对位置编码 p j p_j pj 被换成相对位置编码 r i − j \textcolor{blue}{r_{i-j}} ri−j,其中 r \textcolor{blue}{r} r 采用了 Transformer 中不需要训练的 sinusoid 编码矩阵。
-
第二,引入两个可学习的参数 u \textcolor{red}{u} u 和 v \textcolor{red}{v} v 来分别替换(c)和(d)中的 p i W Q p_iW^Q piWQ。因为对所有的查询位置,查询向量是一样;即无论查询位置如何,对不同词的注意力偏置应保持一致。
-
最后,将 W K W^K WK 拆分为两个权重矩阵 W K , E \textcolor{green}{W^{K,E}} WK,E 和 W K , R \textcolor{green}{W^{K,R}} WK,R,即分别为基于内容的 key 向量和基于位置的 key 向量。
通过修改之后,式(1.11)中每个部分都有了其含义:(a)项表示基于内容的寻址(没有考虑位置编码);(b)项表示相对于内容的位置偏差;(c)项表示全局的内容偏置(从内容层面衡量键的重要性);(d)项表示全局的位置偏差(从相对位置层面衡量键的重要性)。
参考:
[1] Attention Is All You Need
[2] BERT(Pre-training of Deep Bidirectional Transformers for Language Understanding)
[3] Self-Attention with Relative Position Representations
[4] Transformer-XL - Attentive Language Models Beyond a Fixed-Length Context
[5] 详解自注意力机制中的位置编码(第一部分)
[6] 详解自注意力机制中的位置编码(第二部分)
[7] 详解Transformer-XL
[8] 让研究人员绞尽脑汁的Transformer位置编码