树
树(Tree)是n(n≥0)个节点的有限集。
在任意一棵树中:
(1)有且仅有一个特定的称为根(Root)的节点;
(2)当n>1时,其余节点可分m(m>0)为个互不相交的有限集T1,T2,...,Tm;
其中每一个集合本身又是一棵树,并且称为根的子树(SubTree)。
Tree:
--------------------
Height=4 Leves=5 Root
Degree=3 Size=26 ↙
___________________17____________ Node Level1
/ / \ ↙
26______ 2 ___9__ ←- Child Level2
/ \ \ / / \
___0 19 _3___ 6 ___21 15 Level3
/ / \ / \ / \
7 _16 _24 _8 10 4 23 Level4
/ \ / / \ / \ / \
5 11 28 13 1 27 29 18 22 Level5
↑ ↑
↑___↑_______↑... Leaf Left Child Right Child
术语
节点:包含一个数据元素及若干指向其子树的分支,又的译成“结点”(Node)
根:树和子树的“顶点”(Root)
度:节点拥有的子树数量称为节点的度(Degree);树的度是指树内个结点的度的最大值
分支节点:度不为0的节点
叶子:没有子树的节点,即它的度为0 (Leaf)
子节点:结点的子树的根称为该节点的孩子(Child)
父节点:对应子节点上一层(level)节点称为该节点的双亲(Parent)
兄弟结点:同一父节点的子节点,互称兄弟(Sibling)
节点的祖先:是从根到该结点所经分支上的所有节点
节点的子孙:以某结点为根的子树中的所有节点
层:从根开始,根为第一层,根的孩子为第二层...(Level)
深度:树中结点的最大层次数,称为树的深度或高度 (Depth or Height)
森林:是很多互不相交的树的集合(Forest)
无序树:树中任意节点的子节点之间没有顺序关系,这种树称为无序树,也称为自由树
有序树:树中任意节点的子节点之间有顺序关系,这种树称为有序树
最大树(最小树):每个结点的值都大于(小于)或等于其子结点(如果有的话)值的树
二叉树
二叉树(Binary Tree)是一种特殊的有序树型结构。
特点:
(1)每个节点至多有两棵子树;
(2)二叉树的子树有左右之分;
(3)子树的次序不能任意颠倒(有序树)。
性质:
(1)在二叉树的第i层上至多有2^(i-1)个节点(i>=1);
(2)深度为k的二叉树至多有2^k-1个节点(k>=1);
(3)对任何一棵二叉树,如果其叶子节点数为N0,度为2的结点数为N2,则N0=N2+1。
特殊二叉树
满二叉树:
所有层的节点都达到最大数量,叶子除外的所有节点都有两个子节点,所有叶子都在最底一层(k)且数目为2^(k - 1)。即深度k且有2^k - 1个节点(叶子“长”满最后一层),或称完美二叉树 (Perfect Binary Tree)
______12_______
/ \
__3__ __5__
/ \ / \
_7 6 _9 11
/ \ / \ / \ / \
13 8 1 4 10 2 0 14
完全二叉树:
如果删除最底一层的所有叶子它就是满二叉树,即除了最后一层,每层节点都达到最大数量 ,即有深度k的个节点数在左闭右开【2^(k-1)+1,2^k-1】区间内。(Complete Binary Tree)
________3______
/ \
___11___ __4__
/ \ / \
14 7 9 13
/ \ / \ /
2 5 8 6 1
完全二叉树性质:
1. 具有N个节点的完全二叉树的深度为[log2 N]+1,其中[x]为高斯函数,截尾取整。
2. 如果对一棵有n个节点的完全二叉树的节点按层序编号(从第一层到最后一层,每层从左到右),则对任一节点,有:
(1)如果i=1,则节点i是二叉树的根,无双亲;如果i>1,则其双亲节点为[i/2];
(2)如果2i>n,则节点i无左孩子;否则其左孩子是节点2i;
(3)如果2i+1>n,则节点i无右孩子;否则其右孩子是节点2i+1。
其他特殊二叉树
排序二叉树
二叉查找树(Binary Search Tree),也称二叉搜索树或有序二叉树
平衡二叉树
左右子树的高度差不大于1的二叉树,且一定有:它的左、右子树也都是平衡二叉树(Self-Balancing Binary Search Tree)
退化树
退化树是每个节点都只有一个孩子的树,孩子或左或右,或称病态树
斜二叉树
一种特殊的退化树,其中全部节点只有左孩子或右孩子,分别称左斜二叉树和右斜二叉树,功能基本上退化到和链表一样了
霍夫曼树
带权路径最短的二叉树称为哈夫曼树或最优二叉树
B树
一种对读写操作进行优化的自平衡的二叉树查找,能够保持数据有序,拥有多余两个子树
堆 heap
binary heap 是一种完全二叉树,除了最底层的叶子节点之外,是填满的;而且最底层的叶子节点从左至右是连续的,不得有空隙。最大堆(最小堆)就是最大(最小)的完全二叉树。
二叉树的遍历
指如何按某种搜索路径巡防树中的每个结点,使得每个结点均被访问一次,而且仅被访问一次。
常见的遍历方法有:先序遍历,中序遍历,后序遍历,层序遍历;一般都使用递归算法来实现。
以满二叉树为例:
_______1________
/ \
__2__ ___3___
/ \ / \
4 5 _6 _7
/ \ / \ / \ / \
8 9 10 11 12 13 14 15
先序遍历
若二叉树为空,为空操作;
否则(1)访问根节点;(2)先序遍历左子树;(3)先序遍历右子树。
遍历结果: 1 [2 [4 8 9] [5 10 11]] [3 [6 12 13] [7 14 15] “根左右”
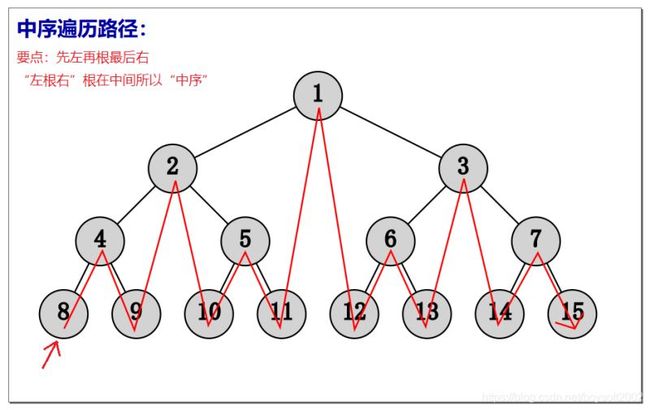
中序遍历
若二叉树为空,为空操作;
否则(1)中序遍历左子树;(2)访问根结点;(3)中序遍历右子树。
遍历结果: [[8 4 9] 2 [10 5 11]] 1 [[12 6 13] 3 [14 7 15]] “左根右”
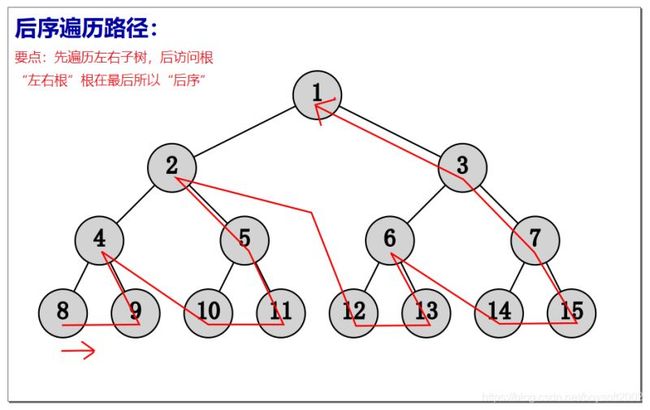
后序遍历
若二叉树为空,为空操作;
否则(1)后序遍历左子树;(2)后序遍历右子树;(3)访问根结点。
遍历结果: [[8 9 4] [10 11 5] 2] [[12 13 6] [14 15 7] 3] 1 “左右根”
层序遍历
若二叉树为空,为空操作;否则从上到下、从左到右按层次进行访问。
遍历结果: 1 [2 3] [4 5 6 7] [8 9 10 11 12 13 14 15]
非满二叉树的遍历结果:
________1________
/ \
__2___ ___3
/ \ / \
4 _5 6 7
\ / \ / \
9 10 11 12 15
先序:1 [2 [4 ' 9] [5 10 11]] [3 [6 12 '] [7 ' 15]]
中序:[' 4 9] 2 [10 5 11] 1 [12 6 '] 3 [' 7 15]
后序:[[' 9 4] [10 11 5] 2] [[12 ' 6] [' 15 7] 3] 1
层序:1 [2 3] [4 5 6 7] [' 9 10 11 12 ' ' 15]
注:结果中 ' 只是标记相对于满二叉树缺失的子节点,实际结果并不展现。
Python 实现二叉树
用Python简单实现如下二叉树的遍历功能,并列出层数和所有叶子:
______A______
/ \
__B__ __C__
/ \ / \
D E F G
/ \ / \ \ \
H I J K L M
代码如下:
class Node():
def __init__(self, data=None, left=None, right=None):
self.data = data
self.left = left
self.right = right
def Preorder(self):
if self.data is not None:
print(self.data, end=' ')
if self.left is not None:
self.left.Preorder()
if self.right is not None:
self.right.Preorder()
def Inorder(self):
if self.left is not None:
self.left.Inorder()
if self.data is not None:
print(self.data, end=' ')
if self.right is not None:
self.right.Inorder()
def Postorder(self):
if self.left is not None:
self.left.Postorder()
if self.right is not None:
self.right.Postorder()
if self.data is not None:
print(self.data, end=' ')
def Height(self):
if self.data is None:
return 0
elif not any([self.left, self.right]):
return 1
elif all([not self.left, self.right]):
return self.right.Height()+1
elif all([self.left, not self.right]):
return self.left.Height()+1
else:
return max(self.left.Height(), self.right.Height())+1
def Leaves(self):
if self.data is None:
return None
elif not any([self.left, self.right]):
print(self.data, end=' ')
elif all([not self.left, self.right]):
self.right.Leaves()
elif all([self.left, not self.right]):
self.left.Leaves()
else:
self.left.Leaves()
self.right.Leaves()
bt = Node('A')
bt.left = Node('B')
bt.right = Node('C')
bt.left.left = Node('D')
bt.left.right = Node('E')
bt.right.left = Node('F')
bt.right.right = Node('G')
bt.left.left.left = Node('H')
bt.left.left.right = Node('I')
bt.left.right.left = Node('J')
bt.left.right.right = Node('K')
bt.right.left.right = Node('L')
bt.right.right.right = Node('M')
print('Perorder:')
bt.Preorder()
print('\nInorder:')
bt.Inorder()
print('\nPostorder:')
bt.Postorder()
print('\nTree Height:\n',bt.Height())
print('\nLeaves:')
bt.Leaves()
运行结果:
Perorder:
A B D H I E J K C F L G M
Inorder:
H D I B J E K A F L C G M
Postorder:
H I D J K E B L F M G C A
Tree Height: # 实为层数,相当于楼房高度地面一层从0计算高度
4
Leaves:
H I J K L M
要实现二叉树完整的所有功能,代码肯定巨长无比。还是找一个优秀的第三方库比较明智!!!
二叉树第三方库 binarytree
使用环境与安装
Requirements: Python 3.6+
Installation:
> pip install binarytreeFor conda users:
> conda install binarytree -c conda-forge
简单实例
binarytree.Node() 二叉树节点
from binarytree import Node root = Node(1) root.left = Node(2) root.right = Node(3) root.left.right = Node(4) print(root) # 或者: root.pprint() # # __1 # / \ # 2 3 # \ # 4 #
binarytree.tree() 随机二叉树
from binarytree import tree bt = tree(is_perfect=True) bt.pprint() # # _______14______ # / \ # ___13__ __8__ # / \ / \ # _9 0 6 3 # / \ / \ / \ / \ # 10 12 5 7 4 2 1 11 #
下一篇准备实战这个第三方库 binarytree !
本文的续篇来了,请点以下链接:
——初步探索二叉树的第三方库 binarytree
总结
到此这篇关于Python二叉树初识的文章就介绍到这了,更多相关Python二叉树初识内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!