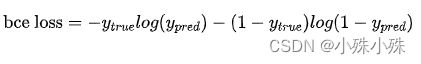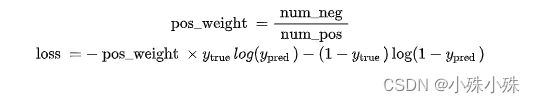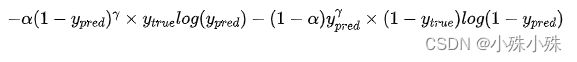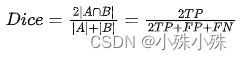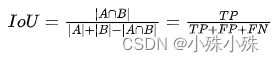语义分割中的 loss function 最全面汇总
目录
一、cross entropy loss
二、weighted loss
三、focal loss
四、dice soft loss
五、soft IoU loss
总结:
一、cross entropy loss
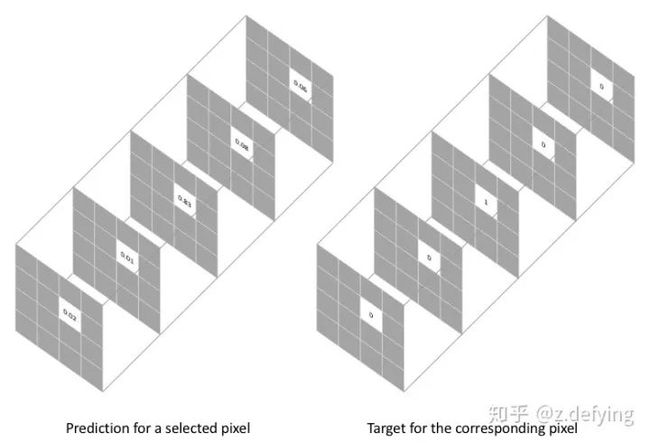
用于图像语义分割任务的最常用损失函数是像素级别的交叉熵损失,这种损失会逐个检查每个像素,将对每个像素类别的预测结果(概率分布向量)与我们的独热编码标签向量进行比较。
假设我们需要对每个像素的预测类别有5个,则预测的概率分布向量长度为5:
每个像素对应的损失函数为:
整个图像的损失就是对每个像素的损失求平均值。
特别注意的是,binary entropy loss 是针对类别只有两个的情况,简称 bce loss,损失函数公式为:
二、weighted loss
由于交叉熵损失会分别评估每个像素的类别预测,然后对所有像素的损失进行平均,因此我们实质上是在对图像中的每个像素进行平等地学习。如果多个类在图像中的分布不均衡,那么这可能导致训练过程由像素数量多的类所主导,即模型会主要学习数量多的类别样本的特征,并且学习出来的模型会更偏向将像素预测为该类别。
FCN论文和U-Net论文中针对这个问题,对输出概率分布向量中的每个值进行加权,即希望模型更加关注数量较少的样本,以缓解图像中存在的类别不均衡问题。
比如对于二分类,正负样本比例为1: 99,此时模型将所有样本都预测为负样本,那么准确率仍有99%这么高,但其实该模型没有任何使用价值。
为了平衡这个差距,就对正样本和负样本的损失赋予不同的权重,带权重的二分类损失函数公式如下:
要减少假阴性样本的数量,可以增大 pos_weight;要减少假阳性样本的数量,可以减小 pos_weight。
三、focal loss
上面针对不同类别的像素数量不均衡提出了改进方法,但有时还需要将像素分为难学习和容易学习这两种样本。
容易学习的样本模型可以很轻松地将其预测正确,模型只要将大量容易学习的样本分类正确,loss就可以减小很多,从而导致模型不怎么顾及难学习的样本,所以我们要想办法让模型更加关注难学习的样本。
对于较难学习的样本,将 bce loss 修改为:
其中的 ![]() 通常设置为2。
通常设置为2。
举个例子,预测一个正样本,如果预测结果为0.95,这是一个容易学习的样本,有 ,损失直接减少为原来的1/400。
而如果预测结果为0.4,这是一个难学习的样本,有 ,损失减小为原来的1/4,虽然也在减小,但是相对来说,减小的程度小得多。
所以通过这种修改,就可以使模型更加专注于学习难学习的样本。
而将这个修改和对正负样本不均衡的修改合并在一起,就是大名鼎鼎的 focal loss:
四、dice soft loss
语义分割任务中常用的还有一个基于 Dice 系数的损失函数,该系数实质上是两个样本之间重叠的度量。此度量范围为 0~1,其中 Dice 系数为1表示完全重叠。Dice 系数最初是用于二进制数据的,可以计算为:
![]() 代表集合A和B之间的公共元素,并且|A|代表集合A中的元素数量(对于集合B同理)。
代表集合A和B之间的公共元素,并且|A|代表集合A中的元素数量(对于集合B同理)。
对于在预测的分割掩码上评估 Dice 系数,我们可以将![]() 近似为预测掩码和标签掩码之间的逐元素乘法,然后对结果矩阵求和。
近似为预测掩码和标签掩码之间的逐元素乘法,然后对结果矩阵求和。
计算 Dice 系数的分子中有一个2,那是因为分母中对两个集合的元素个数求和,两个集合的共同元素被加了两次。为了设计一个可以最小化的损失函数,可以简单地使用 。这种损失函数被称为 soft Dice loss,这是因为我们直接使用预测出的概率,而不是使用阈值将其转换成一个二进制掩码。
Dice loss是针对前景比例太小的问题提出的,dice系数源于二分类,本质上是衡量两个样本的重叠部分。
对于神经网络的输出,分子与我们的预测和标签之间的共同激活有关,而分母分别与每个掩码中的激活数量有关,这具有根据标签掩码的尺寸对损失进行归一化的效果。
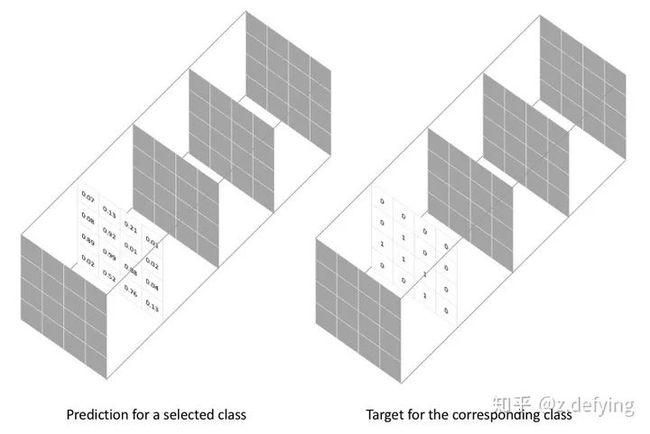
对于每个类别的mask,都计算一个 Dice 损失:
将每个类的 Dice 损失求和取平均,得到最后的 Dice soft loss。
下面是代码实现:
def soft_dice_loss(y_true, y_pred, epsilon=1e-6):
'''
Soft dice loss calculation for arbitrary batch size, number of classes, and number of spatial dimensions.
Assumes the `channels_last` format.
# Arguments
y_true: b x X x Y( x Z...) x c One hot encoding of ground truth
y_pred: b x X x Y( x Z...) x c Network output, must sum to 1 over c channel (such as after softmax)
epsilon: Used for numerical stability to avoid divide by zero errors
# References
V-Net: Fully Convolutional Neural Networks for Volumetric Medical Image Segmentation
https://arxiv.org/abs/1606.04797
More details on Dice loss formulation
https://mediatum.ub.tum.de/doc/1395260/1395260.pdf (page 72)
Adapted from https://github.com/Lasagne/Recipes/issues/99#issuecomment-347775022
'''
# skip the batch and class axis for calculating Dice score
axes = tuple(range(1, len(y_pred.shape)-1))
numerator = 2. * np.sum(y_pred * y_true, axes)
denominator = np.sum(np.square(y_pred) + np.square(y_true), axes)
return 1 - np.mean(numerator / (denominator + epsilon)) # average over classes and batch
五、soft IoU loss
前面我们知道计算 Dice 系数的公式,其实也可以表示为:
其中 TP 为真阳性样本,FP 为假阳性样本,FN 为假阴性样本。分子和分母中的 TP 样本都加了两次。
IoU 的计算公式和这个很像,区别就是 TP 只计算一次:
和 Dice soft loss 一样,通过 IoU 计算损失也是使用预测的概率值:
其中 C 表示总的类别数。
总结:
交叉熵损失把每个像素都当作一个独立样本进行预测,而 dice loss 和 iou loss 则以一种更“整体”的方式来看待最终的预测输出。
这两类损失是针对不同情况,各有优点和缺点,在实际应用中,可以同时使用这两类损失来进行互补。