GNN推荐算法（四）—LESSR：Handling Information Loss of Graph Neural Networks for Session-based Recommen

1 一点点引入

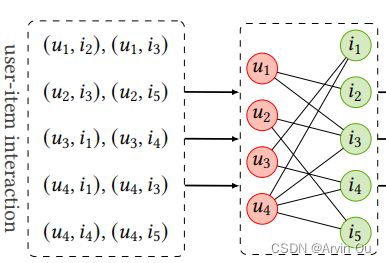
LESSR（Lossless Edge-order preserving aggregation and Shortcut graph attention for Session-based Recommendation) 算法与之前讲到的LR-GCN、LightGCN以及Multi-GCCF算法针对的需求不同。后三个算法基于user-item二分图的结构为user做出推荐，而LESSR则是要通过挖掘用户历史行为的时序模式来预测用户下一时刻的行为。
换句话说就是：根据用户某一段时间内的消费习惯，判断用户下一次会买什么商品。

从数据层面来看可能会更清晰，LESSR面向的是时序数据，如下图用户接触item是有顺序的，

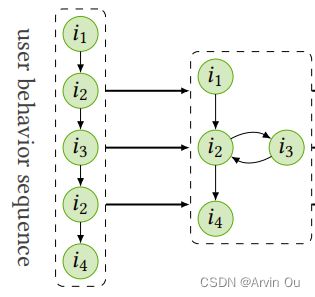
而LR-GCN、LightGCN以及Multi-GCCF等协同过滤算法面向的是user-item二分网络，没有将时间因素考虑在内。

更进一步，基于时序数据的推荐可以细分出session-based recommender，该任务将用户的行为分为若干个不相交的session，然后仅使用active session的历史行为来做出预测。这里所说的session其实就是时间上相近的item序列。

Session-based recommender的理论依据为：相较与session间的依赖，session内的依赖对于下一时刻的行为有更大的影响力。换句话说就是，用户在同一个session中一般有相似的目标。比如，在买完手机后，接下来的购买行为就很有可能是买一些手机配件，而在另一个session中就有可能是买衣服等与手机无关的商品。

Session-based recommendation本质上可以抽象为一个图分类问题，因为每个session都可以转化为一个图，如下所示：

最终目的是要为每个session生成一个保留session全局行为偏好的embedding，基于session的embedding做出推荐。令$I=\{v_1,v_2,...,v_{|I|}\}$为item集合，$s_i=[s_{i,1},s_{i,2},...,s_{i,l_i}]$为第$i$个session，其中$s_{i,t}$代表第$t$时刻$s_i$的item，模型的目标是要预测$s_{i,l_i+1}$，即下一时刻用户可能会点击什么item。通常情况下，模型会输出一个概率分布$p(s_{i,l_i+1}|s_i)$，选择前$K$个概率最高的候选集合做为推荐。

具体地，获得了session embedding之后，就可以计算下一个item的概率分布，首先利用$I$中的item embedding与session embedding计算一个内积（个人觉得可以理解为判断item是不是符合这个session的偏好）
$$z_i=s_h^T{v}_i$$
然后使用softmax输出概率：
$${\hat{y}}_i=\frac{exp(z_i)}{{\sum }_{j\in I}exp(z_j)}$$
最后根据概率从高到底依次推荐。

在模型训练过程中，由于是图分类问题，所以使用的损失函数为交叉熵损失：
$$L(y,\hat{y})=-y^{T}log\hat{y}$$
准备好了吗，一起来看看LESSR到底是怎么做的吧！

P.S. 小伙伴们看完有收获可以帮忙点个赞嘛，也给我一些动力 ^_ ^！

2 LESSR一瞥

基于GNN的时序推荐模型节点embedding更新机制如下：
$$x_i^{(l+1)}=f_{upd}^{(l)}(x_i^{(l)},ag{g}_i^{(l)})$$

$$ag{g}_i^{(l)}=f_{agg}^{(l)}(\{f_{msg}^{(l)}(x_i^{(l)},x_j^{(l)}):(j,i)\in E_{in}(i)\})$$

其中，$x_i^{(l)}$为节点$i$在第$l$层的embedding，$E_{in}(i)$为节点$i$的入连边集合，$f_{msg}$用于计算邻居向目标节点传递的信息，$f_{agg}$为信息聚合函数，$f_{upd}$为embedding更新函数。

在每个节点经过$L$层embedding更新之后，使用一个$readout$函数来获得图的嵌入表示：
$$h_G=f_{out}(\{x_i^{(L)}:i\in V\})$$
LESSR主要是在基于session生成图的方法上做了创新，提出了两种构图方法，下面来简单了解一下：
作者提出普通的构图方法主要有两个信息流失问题：

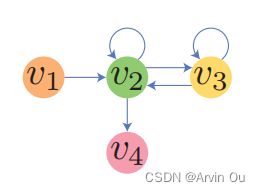
1. Lossy session encoding在将session转换为网络的时候，会丢失序列信息，比如$[v_1,v_2,v_3,v_3,v_2,v_2,v_4]$和$[v_1,v_2,v_2,v_3,v_3,v_2,v_4]$都可以转化为下图：
   
   但根据上图图，我们没办法还原到原始的session。当两个session所指向的下一个item不同时，基于此种构图方法的算法很难做出准确预测。

2. ineffective long-range dependency capturing：一个GNN层可以捕捉到一阶邻居。由于GNN的层数不是越深越好，所以导致GNN-based算法很难捕捉到长序列依赖。

原文：

The second information loss problem is called the ineffective long-range dependency capturing problem where these GNN-based methods cannot effectively capture all long-range dependencies. In each layer of a GNN model, information carried by nodes are propagated along the edges for one step1 , so each layer can capture only 1-hop relation. By stacking multiple layers, the GNN model can capture up to 퐿-hop relation where L is equal to the number of layers. Since stacking more layers do not necessarily increase performance due to the overfitting and over-smoothing problems, the optimal number of layers for these GNN models is usually no larger than 3. Therefore, the models can only capture up to 3-hop relation. However, in real world applications, the session length can easily be larger than 3. Thus, it is very likely that there are some important sequential patterns that are longer than 3. Nevertheless, due to the limitation of the network structure, these GNN-based model cannot capture such information.

关于第二个局限性我存在质疑，如果是GCN的话，虽然第一层仅可以聚合到一阶邻居的信息，但是第二层GCN就是在已经可以涉及到三阶邻居了，也就是说并不是一层只能聚合到更高一阶的信息。

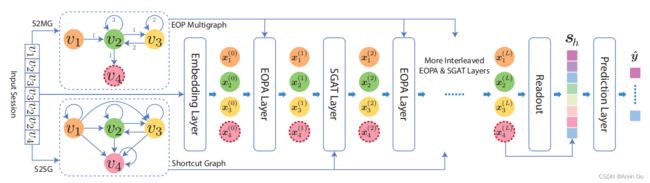
为了解决上述两个问题，作者提出了LESSR，模型中用的属性信息为item的ID。总体框架如下：

2.1 Sessions变网络

为了避免session变网络过程中的时序信息丢失，作者使用了**S2MG（Session to EOP Multigraph）**建立网络，具体如下：

通过为连边增加顺序标签来确保网络可以重构回session。以$[v_1,v_2,v_3,v_3,v_2,v_2,v_4]$为例，可以转换为：

重构的过程如下：节点$v_4$为最后的节点，其上一个节点为$v_2$，因此可以得到$(v_2,v_4)$，此时$v_2$变成了最后的节点，根据入连边的标签，可以得到$(v_2,v_2,v_4)$，以此可以重构。

为解决ineffective long-range dependency问题，作者使用了Session to Shortcut Graph方法来构建网络，其基本思想体现在这个shortcut一词上，即直接在部分原本不相连的节点间增加连边，使得在信息传递过程中，这些节点间的信息可以走近道（shortcut）更快得传过来。具体如下：

当$s_{i,t_1}=u,s_{i,t_2}=v$且$t_1<t_2$时，为每个节点对$(u,v)$添加连边，并且为每个节点添加自环，$[v_1,v_2,v_3,v_3,v_2,v_2,v_4]$如下图所示

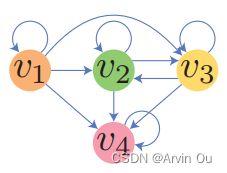
2.2 Edge-Order Perserving Aggregation(EOPA)层

有很多GNN-based方法采用permutation-invariant聚合的思想，忽略了连边的相对顺序。因此作者提出了EOPA层，使用GRU来聚合邻居节点的信息。具体地，令$O{E}_{in}(i)=[(j_1,i),(j_2,i),...,(j_{d_i},i)]$是有序的连边集合，其中$d_i$为节点$i$的度值，聚合公式如下：
$$x_i^{(l+1)}=W_{upd}^{(l)}(x_i^{(l)}||h_{d_i}^{(l)})$$

$$h_k^{(l)}=GR{U}^{(l)}(W_{msg}^{(l)}{x}_{jk}^{(l)},h_{k-1}^{(l)})$$

其中，$\{h_k^{(l)}:0<=k<=d_i\}$为$GRU$的隐层状态，$h_o^{(l)}$为一个零向量，$W_{msg}$为权重矩阵。作者选择GRU的原因是在session-based recommendation上GRU的表现LSTM比好。

2.3 Shortcut Graph Attention(SGAT)层

作者认为在电商类网站上，一个session的长度通常在3以上，而GNN一旦堆得过深（大于3层），效果有可能会更差。那么此时再使用普通的GNN就难以聚合到这么长时间的信息了。因此，作者提出了SGAT层，也就是通过在部分原本不直接相连的节点之间增加连边以使信息可以更快速的传递，公式如下：
$$x_i^{(l+1)}=\sum _{(j,i)\in E_{in}(i)}{a}_{ij}^{(l)}{W}_{val}^{(l)}{x}_j^{(l)}$$

$$a_i^{(l)}=softmax(e_i^{(l)})$$

$$e_{ij}^{(l)}=(p^{(l)}{)}^T\sigma (W_{key}^{(l)}{x}_i^{(l)}+W_{qry}^{(l)}{x}_j^{(l)}+b^{(l)})$$

其中，$p^{(l)}$和$b^{(l)}\in {\mathbf{R}}^d$。

2.4 整体结构

作者在设计模型整体结构的时候会涉及到如何排列EOPA层和SGAT层。作者采用一层EOPA，一层SGAT交互的形式，原因如下：

1. SGAT层会产生信息的丢失，如果连续堆多个SGAT层，信息丢失会更严重。
2. 两两交互可以互相使用到不同层产出的embedding。

另外，作者取消了全连接操作，每一层的输入都是前面所有层输出的拼接。

2.5 生成Session embedding

得到每个节点的表示之后，使用一个注意力机制聚合节点的表示以获得网络的表示，公式如下：
$$h_G=\sum _{i\in V}{\beta }_i{x}_i^{(L)}$$

$$\beta =softmax(ϵ)$$

$${ϵ}_i={\mathbf{q}}^T\sigma (W_1{x}_i^{(L)}+W_2{x}_{last}^{(L)}+r)$$

其中，$q,r\in {\mathbf{R}}^d$。

网络的表示捕捉到了整个session的一个偏好，由于已有研究表明，显示地考虑用户近期兴趣对于推荐有较好的作用，因此作者定义了一个局部偏好向量$s_l=x_{last}^{(L)}$
$$s_h=W_h(h_G||s_l)$$

3 效果如何

作者首先和baseline模型进行了对比：

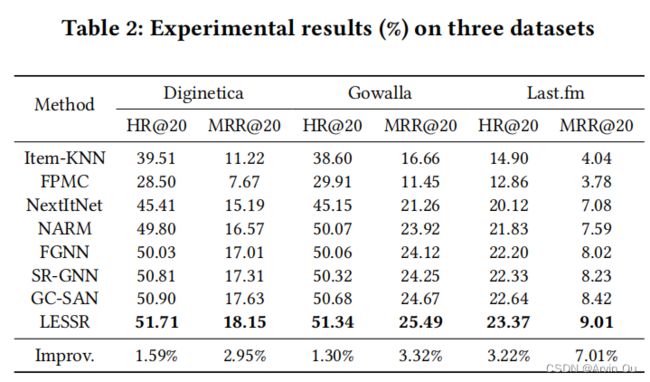
由上表可以看到，以HR@20和MRR@20为平均指标，LESSR是最优的。接着作者对比了EOPA层的有效性：

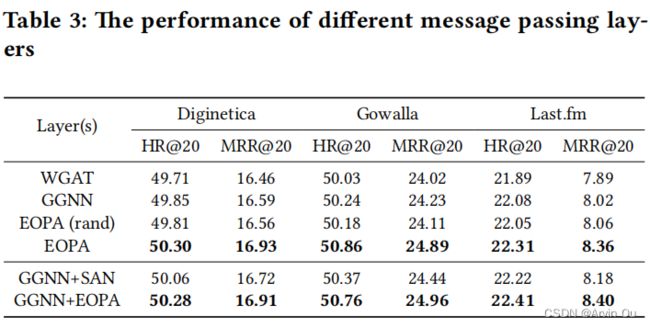
可以看到，加了EOPA对于模型的性能是有一些提升的。

然后作者测试了一下关于EOPA层和SGAT层如何排列：

由此可知，ESES是最好的组合。

最后在三个数据集上测试了不同embedding大小和模型层数对模型表现的影响：

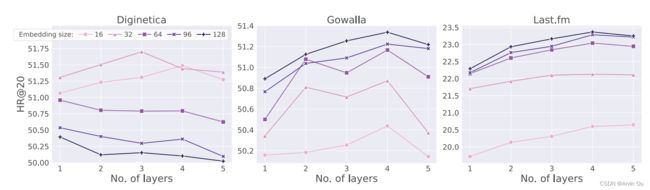
由图可见，针对不同数据embedding大小和层数对准确性的影响还是比较明显的。

4 总结

看完‘Handling Information Loss of Graph Neural Networks for Session-based Recommendation’ 这篇文章后有以下几点收货：

1. 把GNN做的更深，一个主要目的是为了聚合到更高阶邻居的信息。这篇文章提供了一个新的思路，通过加上一个shortcut可以起到同样的效果，不经感叹，妙啊~
2. session based recommender一个基本思路就是把每个session映射成图，然后学习图的embedding，保留整个session的偏好，再比较每个item与各个session的相似性，基于这个相似性去做推荐。
3. 关于GNN无法聚合到长时间信息的局限性我觉得还是有些疑惑，个人认为不同场景的session平均长度必然不同。比如，购买商品和听音乐，一般一天里面购买十几二十几个商品还是比较少的，但一天听十几二十首音乐是很正常的，所以在session比较短的场景继续使用文中说的SGAT一定会提升效果吗？

参考资料

1. Handling Information Loss of Graph Neural Networks for Session-based Recommendation