自组织映射 (SOM) 解决旅行商问题 (TSP)
以下是神经网络求解TSP问题的实验报告，实验中用到了SOM（自组织映射）对TSP（旅行商）问题进行求解，用TSP标准数据集进行了多次实验，取得了不错的效果。
1.问题描述
旅行商问题（Travelling Salesman Problem, 简记TSP，亦称货郎担问题)：设有n个城市和距离矩阵D=[dij]，其中dij表示城市i到城市j的距离，i，j=1，2 … n，则问题是要找出遍访每个城市恰好一次的一条回路并使其路径长度为最短。
2.算法设计
本文采用的神经网络算法为SOM。自组织映射（SOM）是一种无监督学习的神经网络。SM自组织映射的结构只有三层，分别是输入层，全连接层，输出层。其中输入层也就是权值矩阵，输出层就是那些特征映射。SOM算法的主要原理就是每次找到离城市最近的神经元，该神经元被称为优胜神经元，然后以该神经元建立一个高斯分布逐渐更新其他神经元的位置，也就是更新输出神经元权值向量，通过不断的迭代，输出神经元会逐渐学习到输入数据背后的模式，在TSP问题中二维城市坐标就是输入数据，城市空间位置就是网络需要学习的模式，在迭代的过程中，为了保证算法的收敛，会更新学习率等参数，最终达到神经元不断的靠近城市，最终输出一条最短城市回路。
算法流程图如下图所示。
其中
（1）随机初始化神经元的位置，使神经元遍布在城市坐标周围。这里神经元的个数采用的是城市个数的八倍。
（2）找到离城市最近的神经元的位置的时候，这里的距离度量采用的是欧式距离。
（3）周围神经元向该被选中的优胜神经元移动的规则：以优胜神经元为中心，建立高斯分布，高斯分布的初始方差为神经元的个数的十分之一，均值为0.以高斯分布让所有的神经元向第（2）中选取的城市移动。具体更新规则：
nt+1=nt+Gσt*d(c,nt) (1)
其中
表示当前神经元，nt 表示上一次迭代的神经元的值，
表示以该神经元为中心的高斯分布，
表示神经元离当前被选中城市的距离。
表示高斯分布的方差，该方差初始化为城市个数的十分之一。
（4）在每一次迭代的过程中，高斯分布的方差在不断的减少，学习率也在不断的减少，当学习率降到一定程度或者达到迭代次数就结束迭代。学习率与方差更新规则如下：
(2)
σ
(3)
其中
在实验中取值为0.99997，
取值为0.9997。
（5）最后最短路径的输出是按照神经元的顺序排序，然后根据神经元的顺序输出城市路径即为最短路径。
3.程序流程
1.以城市个数的八倍的随机神经元的位置
2.随机挑选一个城市
3.用欧式距离找到距离这个城市最近的神经元。
4.以该神经元为中心，均值为0，方差为城市个数的十分之一创建高斯分布，所有神经元按照该高斯分布向选中的城市移动
5.改变学习率，改变高斯分布的方差
6.判断方差或者学习率是否达到阈值，或者是否达到迭代次数，如果达到则停止迭代，转到步骤7，否则转到步骤2
7.按照神经元的顺序输出城市编号即为最短路径，同时输出最短路径长度。
4.核心伪代码
实验中用到的数据为TSP标准数据集，自行下载
import numpy as np
import random
import math
import re
import matplotlib.pyplot as plt
def get_neighborhood(center, radix, domain):
if radix < 1:
radix = 1
deltas = np.absolute(center - np.arange(domain))
distances = np.minimum(deltas, domain - deltas)
return np.exp(-(distances*distances) / (2*(radix*radix)))
def main(data_path):
with open(data_path, 'r', encoding='UTF-8') as f:
lines = f.readlines()
citys = []
lr = 0.8
start = 0
for line in lines[0:-1]:
start = start + 1
if line.find('NODE_COORD_SECTION') != -1:
break
for line in lines[start:-1]:
try:
if line=="\n" or line.find("EOF") != -1:
continue
cord = line.replace('\n', '')
cord = cord.strip()
cord = re.sub(' +', ' ', cord)
cord = cord.split(' ')
citys.append([int(cord[0]), float(cord[1]), float(cord[2])])
except:
print(line)
n = len(citys)*8
citys = np.array(citys)
temp_citys = citys.copy()
#normalize
x_min, y_min = citys.min(axis=0)[1:]
x_max, y_max = citys.max(axis=0)[1:]
citys[:,1] = (citys[:,1]-x_min)/(x_max-x_min)
citys[:,2] = (citys[:,2]-y_min)/(y_max-y_min)
# for i in range(len(citys)):
# citys[i][1], citys[i][2] = (citys[i][1]-min_c)/(max_c-min_c), (citys[i][2]-min_c)/(max_c-min_c)
network = np.random.rand(n, 2)
iterations = 100000
for i in range(iterations):
#随机选择一个城市
select_city = random.randint(0,len(citys)-1)
city = citys[select_city][1:]
#找到与被选中城市距离最小的神经元
nearest_n = -1
min_dis = float('inf')
for j in range(len(network)):
dis = math.sqrt(sum(pow(city - network[j], 2)))
if dis < min_dis:
min_dis = dis
nearest_n = j
#以该神经元为中心建立高斯分布
gaussian = get_neighborhood(nearest_n, n // 10, network.shape[0])
network += gaussian[:, np.newaxis] * lr * (city - network)
n = n * 0.9997
lr = lr * 0.99997
if i%1000 == 0:
plt.scatter(citys[:,1], citys[:,2], color='red', s=4)
plt.plot(network[:,0], network[:,1], 'r.', ls='-', color='#0063ba', markersize=2)
plt.savefig('./result/iter{}.jpg'.format(i), bbox_inches='tight', pad_inches=0, dpi=200)
plt.close()
if n < 1:
print('Radius has completely decayed, finishing execution',
'at {} iterations'.format(i))
break
if lr < 0.001:
print('Learning rate has completely decayed, finishing execution',
'at {} iterations'.format(i))
break
plt.scatter(citys[:,1], citys[:,2], color='red', s=4)
plt.plot(network[:,0], network[:,1], 'r.', ls='-', color='#0063ba', markersize=2)
plt.savefig('./result/iter{}.jpg'.format(iterations), bbox_inches='tight', pad_inches=0, dpi=200)
plt.close()
new_citys = []
for i in range(len(citys)):
city = citys[i][1:]
nearest_city = -1
min_dis = float('inf')
for j in range(len(network)):
dis = math.sqrt(sum(pow(city - network[j], 2)))
if dis < min_dis:
min_dis = dis
nearest_city = j
new_citys.append([i, nearest_city])
new_citys_ = sorted(new_citys, key=lambda x:x[1])
new_citys_.append(new_citys_[0])
new_citys_ = np.array(new_citys_)
final_path = temp_citys[new_citys_[:,0],:][:,1:]
path_lenght = 0
for i in range(len(final_path)-1):
path_lenght += math.sqrt(sum(pow(final_path[i] - final_path[i+1], 2)))
print('final distance:{}'.format(path_lenght))
plt.scatter(final_path[:, 0], final_path[:, 1], color='red', s=4)
plt.plot(final_path[:, 0], final_path[:, 1], 'r.', ls='-', color='#0063ba', markersize=2)
plt.savefig('./result/route.jpg', bbox_inches='tight', pad_inches=0, dpi=200)
plt.close()
if __name__ == '__main__':
data_path = '../data/a280.tsp'
main(data_path)
5.代码运行及测试
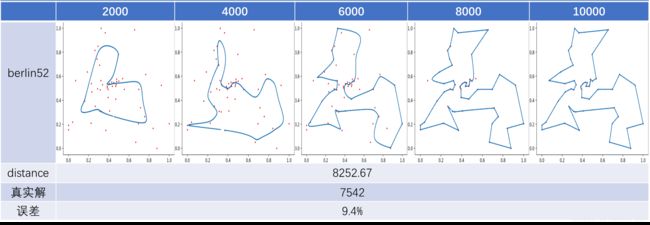
实验中采用的数据为TSP数据集，下图是选用TSP数据集中的berlin52.tsp测试的结果，该tsp包含了52个城市的坐标。实验中的学习率初始值为0.8，高斯分布的方差初始值为城市的个数。
从图中可以很明显的看出，当差不多10000次的时候，就已经找到最优的路径了，证明了该算法的收敛性还是蛮高的。同时也可以看出随着迭代次数的增长，神经元确实在学习输入城市坐标信息，最后基本都靠近于周围的城市位置，最后得到了城市路径连线。实验中得到的距离为8252，真实解为7542，误差为9.4%，证明了实验的解还是比较优化的。
为了进一步分析SOM对于求解TSP问题的优劣情况，实验中选取了不同城市个数以及不同最优解的TSP数据集中的数据，得到如下图的实验结果。
从以上实验图中可以看出，当城市的分布比较简单的时候，无论是最优路径长还是短，SOM都可以得到较好的结果，最终的误差也会变得比较小，比如对于att48,d198，路线都比较简单，即城市的分布比较简单，虽然最终的路线比较长，但是网络仍然可以学习到城市的坐标分布。但是对比于后面的kroB150与a280，无论真实解的长度是大还是小。SOM都无法学习到城市位置分布，所以误差就会变得比较大，根据实验结果可以看出误差一般都早15%左右。
从整个实验中可以看出SOM这种自组织映射的网络对已解决TSP问题还是很有效的，特别是对于那些城市分布不太复杂的，网络往往可以学习到城市的位置信息，并且达到快速收敛的效果，最后得到较优化的路径。但是从实验中也可以看出，如果城市分布比较复杂的话，网络就比较难学习该分布，导致最终的误差比较大。
6.结论
旅行商问题属于NP难问题，无法在线性的复杂度中求解。自组织映射（SOM）是一种无监督学习的神经网络，将各个城市的坐标作为输入之后，该网路的神经元通过高斯分布不断的靠近城市坐标的位置，从而不断学到了输入数据的模式，最后得到了一条优化的最短城市路径。通过实验结果可以看出该方法在求解TSP问题上往往可以得到比较优化的解，与真实解相差不大。
但是利用SMO求解的话，神经元的个数将会随着城市的个数飞速上涨，进而导致搜索速度很慢，而且由于网络的随机性，网络有时候也会陷入到一个局部最优解中，针对以上问题都是以后需要去研究的方向。
参考：https://zhuanlan.zhihu.com/p/34121865