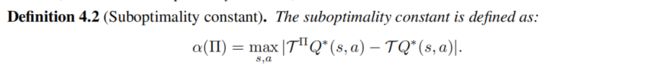离线强化学习(Offline RL)系列3: (算法篇)策略约束 - BEAR算法原理详解与实现

论文信息：Stabilizing Off-Policy Q-Learning via Bootstrapping Error Reduction

本文由UC Berkeley的Sergey Levine团队(Aviral Kumar)于2019年提出，并发表在NIPS2019会议上，是一篇在Scott Fujimoto的BCQ算法基础上，另辟蹊径的提出的一种经典的解决Offline RL中累计误差的文章，文章理论分析非常扎实，同时作者也全部opensource了代码，非常推荐研究。

摘要：策略约束（Policy constraint）作为一种非常重要的约束方法广泛的用在强化学习领域，比如online学习中TRPO、PPO， ACKER等，以及离线强化学习中的BCQ算法。然而，在offline中，BCQ使用的VAE和生成扰动网络虽然解决了extrapolation error,但对于一些仍然处于行为策略分布外（Out-of- Distributuin, OOD）的状态-动作无法很好的拟合，本文阐述的BEAR算法是一种新的策略约束解决办法，其通过一种交Support-set matching技术解决了learned policy和behavior policy之间的关系，达到了一种state of the art的效果。

1. 前言(约束方法回顾)

在离线强化学习(Offline RL)中，策略约束（Policy Constraint）方法通常分为四大类：

• 显式f-散度约束（Explict f-divergence constraint）
• 隐式f-散度约束（Implict f-divergence constraint）
• 积分概率度量约束(Integral probability metric, IPM)
• 策略惩罚(policy penalty)

本篇博文将首先回顾一下Online的TRPO、PPO的约束方法，以及Offline的BCQ方法，然后接着产阐述基于策略约束的BEAR（Bootstrapping error accumulation reduction）算法。

1.1 TRPO约束方法

TRPO [1]为了让学习的新策略 ${\pi }_{new}$ 和旧策略 ${\pi }_{old}$ 之间保持一个安全距离，作者通过使用KL散度去约束两个学习分布之间的距离来提高学习的效率，Objective函数如下所示：
$$\begin{array}{rl}& \underset{\theta }{\mathrm{maximize}}{\mathbb{E}}_{s\sim {\rho }_{{\theta }_{\text{old }}},a\sim q}\left[\frac{{\pi }_{\theta }(a\mid s)}{q(a\mid s)}{Q}_{{\theta }_{\text{old }}}(s,a)\right]\\ & \text{ subject to }{\mathbb{E}}_{s\sim {\rho }_{{\theta }_{\text{old }}}}\left[D_{\mathrm{K}\mathrm{L}}\left({\pi }_{{\theta }_{\text{old }}}(\cdot \mid s)\Vert {\pi }_{\theta }(\cdot \mid s)\right)\right]\le \delta \end{array}$$

通过公式变换，最终需要解决如下问题
$$\underset{\theta }{\mathrm{maximize}}{\hat{\mathbb{E}}}_t\left[\frac{{\pi }_{\theta }\left(a_t\mid s_t\right)}{{\pi }_{{\theta }_{\text{old }}}\left(a_t\mid s_t\right)}{\hat{A}}_t-\beta \mathrm{K}\mathrm{L}\left[{\pi }_{{\theta }_{\text{old }}}\left(\cdot \mid s_t\right),{\pi }_{\theta }\left(\cdot \mid s_t\right)\right]\right]$$
详细过程请参阅： 深度强化学习系列(15): TRPO算法原理及Tensorflow实现

1.2 PPO约束方法

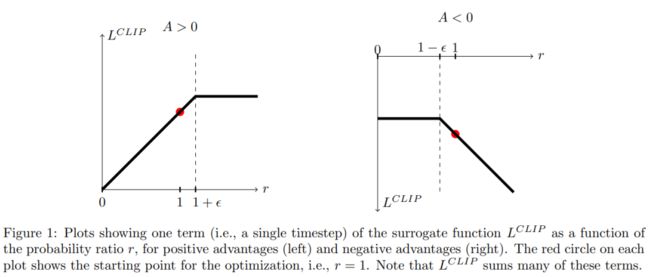
为了解决1.1 TRPO中的 $\beta$ 难以选择的问题，作者直接短平快的使用了clip方法。
$$L^{CLIP}(\theta )={\hat{\mathbb{E}}}_t\left[\min \left(r_t(\theta ){\hat{A}}_t,\mathrm{clip}\left(r_t(\theta ),1-ϵ,1+ϵ\right){\hat{A}}_t\right)\right]$$

1.3 BCQ约束方法

具体详见博客: 离线强化学习(Offline RL)系列3: (算法篇)BCQ算法原理及实现详解

本文是在上一篇博客BCQ算法基础上的工作，BCQ算法为了解决extrapolation error主要做了一件事，即通过VAE和生成扰动网络来生成训练动作（策略），使得其接近行为策略（有那么点模仿学习的画风），但问题是全部靠近了行为策略并一定好，如果一条trajectory是以前从未见到多的，可能就会没法学习。

2. Offline RL误差的来源

2.1 分布偏移(distribution shift)

分布偏移最主要的原因是learned policy 和 behavior policy之间的偏移（从图中我们可以清晰的看到两者之间的区别），这也是offlineRL相比于Online RL在不能交互学习的情况下造成的。

2.2 OOD(out-of-distribution) action问题

OOD问题在Offline RL中非常常见，简单的可以理解为状态-动作对可能不在我们的offline Dataset中，对应的分布也一样，即学习分布远在（far outside）训练（training distribution）分布之外。

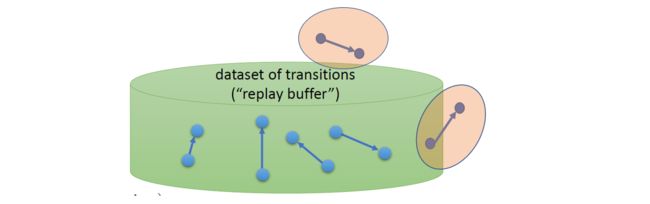
那么训练和优化过程如下：

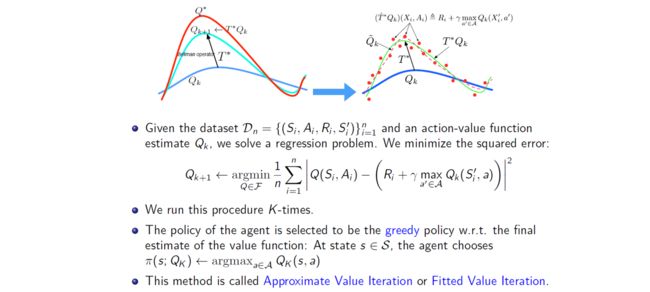
结合上图，其实真正解决这个问题，第一直观的想法就是增大数据集的数量，让数据集尽可能包含训练分布,这样学习分布基本可能会在范围内，然而这个方法并不奏效：

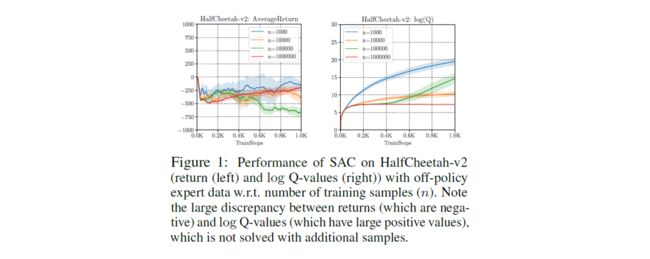
作者在实验中使用了大小不一样的数量实验，结果表明即使增大train samples, 算法的性能并没有得到有效提升，同时也会引发下一个累计误差问题：

此外Q值误差居高不下，是什么原因造成的？

2.3 贝尔曼误差（Bellman error）

这就是本文的核心问题了，深度强化学习中动态规规划（MC，TD）最核心的就是Q函数，我们知道在Q-learning中学习的时候，目标函数Q的计算通常是利用自举(bootstrapping)的方式，从训练集分布中去最大化函数估计，但由于OOD之外的数据，导致这个过程的error不断累积，最终导致严重偏离学习策略。

我们在Online RL中知道，最优 $Q$ 函数 $Q^{\ast }$ 遵循最优贝尔曼方程，如下所示：
$$Q^{\ast }={\mathcal{T}}^{\ast }{Q}^{\ast };\left({\mathcal{T}}^{\ast }\hat{Q}\right)(s,a):=R(s,a)+\gamma {\mathbb{E}}_{T\left(s^{\prime }\mid s,a\right)}\left[\underset{a^{\prime }}{\max }\hat{Q}\left(s^{\prime },a^{\prime }\right)\right]$$
然后，强化学习对应于最小化该等式左侧和右侧之间的平方差，也称为均方贝尔曼误差 (MSBE)，得到：

$$Q:=\arg \underset{\hat{Q}}{\min }{\mathbb{E}}_{s\sim \mathcal{D},a\sim \beta (a\mid s)}\left[{\left(\hat{Q}(s,a)-\left({\mathcal{T}}^{\ast }\hat{Q}\right)(s,a)\right)}^2\right]$$

MSBE 在由行为策略 $\beta (a|s)$ 生成的数据集 $D$ 中的转换样本上最小化。 尽管最小化 MSBE 对应于有监督的回归问题，但该回归的目标本身是从当前 $Q$ 函数估计中得出的。于是对于迭代 $k$ 次的Q-learning来说，总误差(error) 可以定义为：
$${\zeta }_k(s,a)=\left|Q_k(s,a)-Q^{\ast }(s,a)\right|$$

其中当前的贝尔曼误差（Bellman error）为：
$${\delta }_k(s,a)=\left|Q_k(s,a)-\mathcal{T}{Q}_{k-1}(s,a)\right|$$

那么我们就可以得出以下结论：
$${\zeta }_k(s,a)\le {\delta }_k(s,a)+\gamma \underset{a^{\prime }}{\max }{\mathbb{E}}_{s^{\prime }}\left[{\zeta }_{k-1}\left(s^{\prime },a^{\prime }\right)\right]$$

所以说，当一个状态-动作分布处于OOD之外时，我们其实是希望 ${\delta }_k(s,a)$ 很高，因为我们的优化目标是不断将处于分布之外的策略分布与训练分布距离最小化。为了缓解这个问题，作者提出了一个解决方法就是让学习策略输出的动作处于训练分布的支撑集（Support-set）中。

所谓的Support-set， 其实就是"学习策略 $\pi (a\mid s)$ 只有在行为策略 $\beta (a\mid s)$ 的密度大于阈值 $\forall a,\beta (a\mid s)\le \epsilon ⟹\pi (a\mid s)=0$，而不是对密度 $\pi (a\mid s)$ 和 $\beta (a\mid s)$ 的值的接近约束。"
原话：

下面我们结合例子解释一下 分布匹配（Distribution-matching 和 支撑集匹配(Support-set matching) 的区别，以及原理。

3. 从一个例子原因分析开始

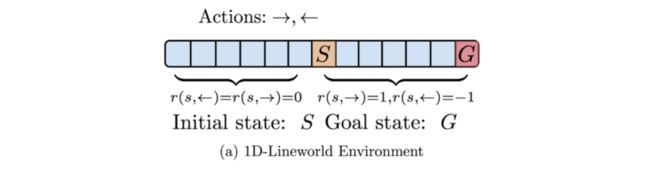
考虑一维的Lineworld Environment问题，我们从 $S$ 点出发到达 $G$ 点，动作集分为“向左”和“向右”两种，对应的奖励在上图中有标记。

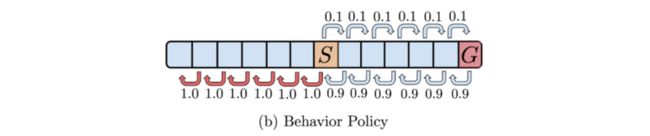
那么，行为策略在 $S$ 和 $G$ 之间的状态下执行次优动作，可能性为 0.9，但是动作 $\leftarrow$ 和 $\to$ 的状态都在分布内（in-distribution）。

个人理解原因

3.1 Distribution-matching

如上图，分布匹配约束（distribution matching constraint）的学习策略可以是任意次优的，事实上，通过推出该策略达到目标 G 的概率非常小，并且随着环境的建立而趋于 0 较大。

3.2 Support-constraint

然而，在support-constraint中，作者表明支持约束可以恢复概率为 1 的最优策略（其实原因很简单，就是阈值 $\forall a,\beta (a\mid s)\le \epsilon ⟹\pi (a\mid s)=0$ 的原因, 只要动作在训练行为策略分布的支持集内就可以）。

那么为什么Distribution-matching在这里会失败？

• 如果惩罚被严格执行，那么智能体将被迫在 $S$ 和 $G$ 之间的状态中主要执行错误的动作 $\leftarrow$，导致次优行为。
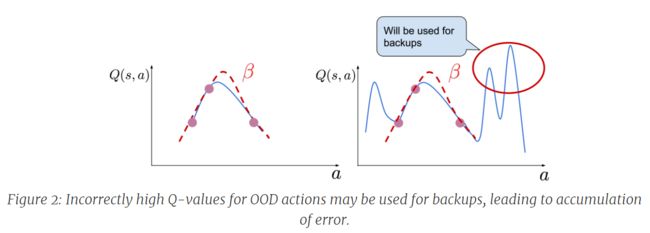
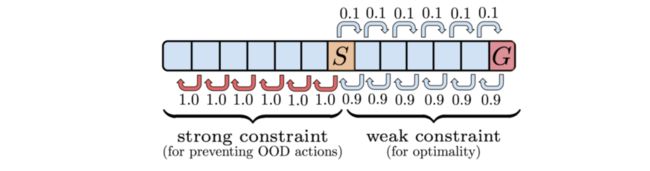
• 如果惩罚没有严格执行，为了实现比行为策略更好的策略，智能体将使用 OOD之外的action $\to$在 $S$ 左侧的状态执行backups，这些backups 最终会影响 状态S下的Q值。这种现象将导致不正确的 Q 函数，从而导致错误的策略——可能是从 S 开始向左移动而不是向 G 移动的策略，因为 OOD 动作backups与高估偏差相结合Q-learning 可能会使状态 S 的动作 $\leftarrow$ 看起来更可取。如下图所示，一些状态需要强惩罚/约束（以防止 OOD backups），而其他状态需要弱惩罚/约束（以实现最优性）才能使分布匹配起作用，但是，这无法通过传统的分布匹配来实现方法。

通过上述分析，我们得出一个结论：我们希望的不是学习策略和行为策略越像越好，而是学习策略能够在行为策略的支撑集的范围内去进行优化， 如果学习策略和行为策略无限接近那不就是Behavior clone了，但offline无法无限的去逼近online，所以问题仍然存在。

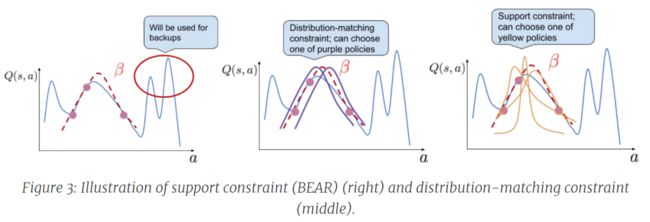
下图就是关于Distribution-matching 和support constraint选择动作的区别

从图中我们可以看到：以红色的行为策略 $\beta$ 为基准，在distribution-matching中则仅有紫色的学习策略相符，但在support-matching中黄色的都是可以匹配的learned policy, 所以更通用。

那么support-set matching更通用，具体是怎么matching的呢？下文我们从论文的理论部分开始分析。

4. 理论设计及分析(核心：建议阅读)

4.1 Support-set Matching(支撑集匹配方法)

4.1.1 支撑集匹配原理

第一步： 解决策略集定义及收敛，定义Distribution-constraint operators概念，如下所示：

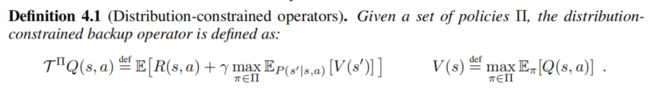
这里面最关键的有以下几个地方：

• 定义了一个策略集 $\prod$ ，且动作空间 $A\in \prod$，而不是定义策略
• 根据原始的MDP问题重新定义了一个新的MDP" 问题，原理和bellman operator一样，同样利用了不动点去证明收敛性。

为了分析在近似误差下执行backup的次优(suboptimality) 问题，作者提出两个方面:

• 次优偏置(suboptimality bias), 也就是最优的学习策略如果在行为策略支撑集之外的话，仍然能够找到次优策略。
• 次优常数（suboptimality constant），分布偏移、OOD之外的次优问题，次优常数相当于做了一个限定（which measures how far ${\pi }^{\ast }$ is from $\prod$）， 【 $\alpha (\Pi )$ 越小，policy set $\prod$ 距离optimal policy ${\pi }^{\ast }$ 的距离越小。】

这里定义了一个Concentrability，【 $C(\Pi )$越小，就说明policy set $\prod$ 中的policy 与 behavior policy $\beta$ 越相似】

第二步：最后作者给出了一个边界（bound）

证明过程如下：

这里的[Error Bounds for Approximate Value Iteration] 中解释了

$${\Pi }_{ϵ}:=\{\pi \mid \pi (a\mid s)=0\text{ whenever }\beta (a\mid s)\le ϵ\}$$

We choose policies only lying in high support regions of the behaviour policy.
Allows for a tradeoff between: Keeping close to the data (minimizing amount of propagated error) Having freedom to find the optimal policy

这里作者不是对所有策略执行最大化，而是对集合 Pi_eps 执行受限最大值，为了实际执行此操作，使用执行支撑匹配的约束。

其中作者原话是：

We change the policy improvement step, where instead of performing a maximization over all policies, we perform the restricted max over the set ${\pi }_{eps}$ and in order to do this practically, we use a constrained formulation, where we use a constraint that performs support matching. We constrain the maximum mean discrepancy distance between the dataset and the actor to a maximal limit, using samples.

4.1.2 为什么要从 ${\Pi }_{ϵ}$ 选取动作？

通过以上的方法，问题最终化解为一个求解最优问题：

4.2 Maximum Mean Discrepancy (MMD)

4.2.1 MMD原理

MMD [A Kernel Two-Sample Test] 方法是一种统计测试以确定两个样本是否来自不同的分布，检验统计量是再现 kernel Hilbertspace (RKHS) 的单位球中函数的最大期望差异。

4.2.2 MMD代码求解

def gaussian_kernel(x, y, sigma=0.1):
  return exp(-(x - y).pow(2).sum() / (2 * sigma.pow(2)))

def compute_mmd(x, y):
  k_x_x = gaussian_kernel(x, x)
  k_x_y = gaussian_kernel(x, y)
  k_y_y = gaussian_kernel(y, y)
  return sqrt(k_x_x.mean() + k_y_y.mean() - 2*k_x_y.mean())

4.2.3 与KL divergence的区别

4.3 双梯度下降(Dual Gradient Descent)(可跳过)

4.3.1 DGD原理及图解[Dual Gradient Descent]

双梯度下降是一种在约束条件下优化目标的流行方法。 在强化学习中，它可以帮助我们做出更好的决策。

5. BEAR算法执行过程

备注这里还有另外一个版本

6. 部分结果分析

7. Pytorch代码实现部分浅析

本代码由原作者开源 [Github]

7.1 Installing & running

python main.py --buffer_name=buffer_walker_300_curr_action.pkl --eval_freq=1000 --algo_name=BEAR
--env_name=Walker2d-v2 --log_dir=data_walker_BEAR/ --lagrange_thresh=10.0 
--distance_type=MMD --mode=auto --num_samples_match=5 --lamda=0.0 --version=0 
--mmd_sigma=20.0 --kernel_type=gaussian --use_ensemble_variance="False"

7.2 MMD&KL loss

 def mmd_loss_laplacian(self, samples1, samples2, sigma=0.2):
        """MMD constraint with Laplacian kernel for support matching"""
        # sigma is set to 10.0 for hopper, cheetah and 20 for walker/ant
        diff_x_x = samples1.unsqueeze(2) - samples1.unsqueeze(1)  # B x N x N x d
        diff_x_x = torch.mean((-(diff_x_x.abs()).sum(-1)/(2.0 * sigma)).exp(), dim=(1,2))

        diff_x_y = samples1.unsqueeze(2) - samples2.unsqueeze(1)
        diff_x_y = torch.mean((-(diff_x_y.abs()).sum(-1)/(2.0 * sigma)).exp(), dim=(1, 2))

        diff_y_y = samples2.unsqueeze(2) - samples2.unsqueeze(1)  # B x N x N x d
        diff_y_y = torch.mean((-(diff_y_y.abs()).sum(-1)/(2.0 * sigma)).exp(), dim=(1,2))

        overall_loss = (diff_x_x + diff_y_y - 2.0 * diff_x_y + 1e-6).sqrt()
        return overall_loss
    
    def mmd_loss_gaussian(self, samples1, samples2, sigma=0.2):
        """MMD constraint with Gaussian Kernel support matching"""
        # sigma is set to 10.0 for hopper, cheetah and 20 for walker/ant
        diff_x_x = samples1.unsqueeze(2) - samples1.unsqueeze(1)  # B x N x N x d
        diff_x_x = torch.mean((-(diff_x_x.pow(2)).sum(-1)/(2.0 * sigma)).exp(), dim=(1,2))

        diff_x_y = samples1.unsqueeze(2) - samples2.unsqueeze(1)
        diff_x_y = torch.mean((-(diff_x_y.pow(2)).sum(-1)/(2.0 * sigma)).exp(), dim=(1, 2))

        diff_y_y = samples2.unsqueeze(2) - samples2.unsqueeze(1)  # B x N x N x d
        diff_y_y = torch.mean((-(diff_y_y.pow(2)).sum(-1)/(2.0 * sigma)).exp(), dim=(1,2))

        overall_loss = (diff_x_x + diff_y_y - 2.0 * diff_x_y + 1e-6).sqrt()
        return overall_loss

    def kl_loss(self, samples1, state, sigma=0.2):
        """We just do likelihood, we make sure that the policy is close to the
           data in terms of the KL."""
        state_rep = state.unsqueeze(1).repeat(1, samples1.size(1), 1).view(-1, state.size(-1))
        samples1_reshape = samples1.view(-1, samples1.size(-1))
        samples1_log_pis = self.actor.log_pis(state=state_rep, raw_action=samples1_reshape)
        samples1_log_prob = samples1_log_pis.view(state.size(0), samples1.size(1))
        return (-samples1_log_prob).mean(1)

7.3 BEAR train

def train(self, replay_buffer, iterations, batch_size=100, discount=0.99, tau=0.005):
        for it in range(iterations):
            state_np, next_state_np, action, reward, done, mask = replay_buffer.sample(batch_size)
            state           = torch.FloatTensor(state_np).to(device)
            action          = torch.FloatTensor(action).to(device)
            next_state      = torch.FloatTensor(next_state_np).to(device)
            reward          = torch.FloatTensor(reward).to(device)
            done            = torch.FloatTensor(1 - done).to(device)
            mask            = torch.FloatTensor(mask).to(device)
            
            # Train the Behaviour cloning policy to be able to take more than 1 sample for MMD
            recon, mean, std = self.vae(state, action)
            recon_loss = F.mse_loss(recon, action)
            KL_loss = -0.5 * (1 + torch.log(std.pow(2)) - mean.pow(2) - std.pow(2)).mean()
            vae_loss = recon_loss + 0.5 * KL_loss

            self.vae_optimizer.zero_grad()
            vae_loss.backward()
            self.vae_optimizer.step()

            # Critic Training: In this step, we explicitly compute the actions 
            with torch.no_grad():
                # Duplicate state 10 times (10 is a hyperparameter chosen by BCQ)
                state_rep = torch.FloatTensor(np.repeat(next_state_np, 10, axis=0)).to(device)
                
                # Compute value of perturbed actions sampled from the VAE
                target_Qs = self.critic_target(state_rep, self.actor_target(state_rep))

                # Soft Clipped Double Q-learning 
                target_Q = 0.75 * target_Qs.min(0)[0] + 0.25 * target_Qs.max(0)[0]
                target_Q = target_Q.view(batch_size, -1).max(1)[0].view(-1, 1)
                target_Q = reward + done * discount * target_Q

            current_Qs = self.critic(state, action, with_var=False)
            if self.use_bootstrap: 
                critic_loss = (F.mse_loss(current_Qs[0], target_Q, reduction='none') * mask[:, 0:1]).mean() +\
                            (F.mse_loss(current_Qs[1], target_Q, reduction='none') * mask[:, 1:2]).mean() 
                            # (F.mse_loss(current_Qs[2], target_Q, reduction='none') * mask[:, 2:3]).mean() +\
                            # (F.mse_loss(current_Qs[3], target_Q, reduction='none') * mask[:, 3:4]).mean()
            else:
                critic_loss = F.mse_loss(current_Qs[0], target_Q) + F.mse_loss(current_Qs[1], target_Q) #+ F.mse_loss(current_Qs[2], target_Q) + F.mse_loss(current_Qs[3], target_Q)

            self.critic_optimizer.zero_grad()
            critic_loss.backward()
            self.critic_optimizer.step()

            # Action Training
            # If you take less samples (but not too less, else it becomes statistically inefficient), it is closer to a uniform support set matching
            num_samples = self.num_samples_match
            sampled_actions, raw_sampled_actions = self.vae.decode_multiple(state, num_decode=num_samples)  # B x N x d
            actor_actions, raw_actor_actions = self.actor.sample_multiple(state, num_samples)#  num)

            # MMD done on raw actions (before tanh), to prevent gradient dying out due to saturation
            if self.use_kl:
                mmd_loss = self.kl_loss(raw_sampled_actions, state)
            else:
                if self.kernel_type == 'gaussian':
                    mmd_loss = self.mmd_loss_gaussian(raw_sampled_actions, raw_actor_actions, sigma=self.mmd_sigma)
                else:
                    mmd_loss = self.mmd_loss_laplacian(raw_sampled_actions, raw_actor_actions, sigma=self.mmd_sigma)

            action_divergence = ((sampled_actions - actor_actions)**2).sum(-1)
            raw_action_divergence = ((raw_sampled_actions - raw_actor_actions)**2).sum(-1)

            # Update through TD3 style
            critic_qs, std_q = self.critic.q_all(state, actor_actions[:, 0, :], with_var=True)
            critic_qs = self.critic.q_all(state.unsqueeze(0).repeat(num_samples, 1, 1).view(num_samples*state.size(0), state.size(1)), actor_actions.permute(1, 0, 2).contiguous().view(num_samples*actor_actions.size(0), actor_actions.size(2)))
            critic_qs = critic_qs.view(self.num_qs, num_samples, actor_actions.size(0), 1)
            critic_qs = critic_qs.mean(1)
            std_q = torch.std(critic_qs, dim=0, keepdim=False, unbiased=False)

            if not self.use_ensemble:
                std_q = torch.zeros_like(std_q).to(device)
                
            if self.version == '0':
                critic_qs = critic_qs.min(0)[0]
            elif self.version == '1':
                critic_qs = critic_qs.max(0)[0]
            elif self.version == '2':
                critic_qs = critic_qs.mean(0)

            # We do support matching with a warmstart which happens to be reasonable around epoch 20 during training
            if self.epoch >= 20: 
                if self.mode == 'auto':
                    actor_loss = (-critic_qs +\
                        self._lambda * (np.sqrt((1 - self.delta_conf)/self.delta_conf)) * std_q +\
                        self.log_lagrange2.exp() * mmd_loss).mean()
                else:
                    actor_loss = (-critic_qs +\
                        self._lambda * (np.sqrt((1 - self.delta_conf)/self.delta_conf)) * std_q +\
                        100.0*mmd_loss).mean()      # This coefficient is hardcoded, and is different for different tasks. I would suggest using auto, as that is the one used in the paper and works better.
            else:
                if self.mode == 'auto':
                    actor_loss = (self.log_lagrange2.exp() * mmd_loss).mean()
                else:
                    actor_loss = 100.0*mmd_loss.mean()

            std_loss = self._lambda*(np.sqrt((1 - self.delta_conf)/self.delta_conf)) * std_q.detach() 

            self.actor_optimizer.zero_grad()
            if self.mode =='auto':
                actor_loss.backward(retain_graph=True)
            else:
                actor_loss.backward()
            # torch.nn.utils.clip_grad_norm(self.actor.parameters(), 10.0)
            self.actor_optimizer.step()

            # Threshold for the lagrange multiplier
            thresh = 0.05
            if self.use_kl:
                thresh = -2.0

            if self.mode == 'auto':
                lagrange_loss = (-critic_qs +\
                        self._lambda * (np.sqrt((1 - self.delta_conf)/self.delta_conf)) * (std_q) +\
                        self.log_lagrange2.exp() * (mmd_loss - thresh)).mean()

                self.lagrange2_opt.zero_grad()
                (-lagrange_loss).backward()
                # self.lagrange1_opt.step()
                self.lagrange2_opt.step() 
                self.log_lagrange2.data.clamp_(min=-5.0, max=self.lagrange_thresh)   
            
            # Update Target Networks 
            for param, target_param in zip(self.critic.parameters(), self.critic_target.parameters()):
                    target_param.data.copy_(tau * param.data + (1 - tau) * target_param.data)

            for param, target_param in zip(self.actor.parameters(), self.actor_target.parameters()):
                    target_param.data.copy_(tau * param.data + (1 - tau) * target_param.data)

参考文献

[1]. Aviral Kumar, Justin Fu, George Tucker, Sergey Levine: “Stabilizing Off-Policy Q-Learning via Bootstrapping Error Reduction”, 2019; arXiv:1906.00949.
[2]. Aviral Kumar: Data-Driven Deep Reinforcement Learning, [EB/OL]Blog, Dec 5, 2019.

---

OfflineRL推荐阅读

离线强化学习(Offline RL)系列3: (算法篇)策略约束-BCQ算法详解与实现
离线强化学习(Offline RL)系列2: (环境篇)D4RL数据集简介、安装及错误解决
离线强化学习(Offline RL)系列1：离线强化学习原理入门